Statistique descriptive
7. Dépendances et causalité
7.2. Les relations de dépendance
Lorsque nous étudions le monde, nous ne pouvons souvent rien faire d'autre que de constater des co-occurrences. La question fondamentale qui se pose alors au chercheur est de savoir passer du constat de cooccurrences à la création d'hypothèses sur le fonctionnement général du monde (c'est ce qu'on appelle l'induction) et comment tester ces hypothèses. Pour le praticien, la question est un peu différente, car les hypothèses générales ont le plus souvent déjà été produites par des chercheurs. Le psychologue ou le médecin n'inventent pas les maladies, ils se contentent de puiser dans leurs connaissances, la pathologie connue qui semble le mieux s'appliquer au cas du patient qu'ils ont en face d'eux. C'est ce qu'on appelle l'abduction. Mais qu'on soit chercheur ou praticien, il va falloir à un moment ou un autre tester les hypothèses. Il faut donc pouvoir vérifier si la relation qu'on suppose entre les variables est plausible ou non.
Concrètement, nous avons deux possibilités extrêmes : soit l'hypothèse d'une relation entre les variables est complètement fausse, soit elle est complètement vraie. Si elle est entièrement fausse, nous aurons ce qui s'appelle l'indépendance des variables. Si elle est entièrement vraie, nous aurons la dépendance parfaite. Examinons maintenant comment ces deux situations extrêmes se traduisent en termes de cooccurrences.
2.1. Dépendance de deux variables
Imaginons deux variables, disons l'âge et le revenu des adultes. Imaginons que ces deux variables soient parfaitement et positivement liées. Cela voudrait dire que plus une personne est âgée, et plus son revenu est élevé. Sous cette hypothèse, je pourrais prendre un échantillon d'adulte et pour chaque individu mesurer son âge et son revenu. Je vais donc disposer d'un ensemble de cooccurrences (de couples de données), une par personne. Par exemple, admettons que dans mon échantillon, les âges aillent de 30 à 50 ans. Admettons encore que les salaires soient répartis en trois catégories, 0 € à 999 € / mois; 1000 € / mois à 1999 € / mois, 2000 € /mois et plus.
Admettons que mes variables soient parfaitement liées, je m'attends à observer qu'à chaque fois que la variable âge est élevée, la variable revenu est élevée aussi. Je peux même observer que si deux individus n'ont pas le même âge, alors le plus âgé a aussi le revenu le plus élevé. Réciproquement, pour toute paire individus, si l'un n'a pas le même revenu que l'autre, alors celui qui a le revenu le plus haut est aussi le plus âgé. Clairement, si la structure des cooccurrences dans mon échantillon obéit à ces propriétés, je pourrai dire que les variables âge et revenu sont positivement liées.
Lorsque l'on se borne à constater la cooccurrence d'événements, on parle souvent alors de loi. Par exemple, la loi de Fechner relie l'intensité perçue d'un son et le logarithme de la puissance physique de ce son :
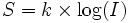
Notons que rien ne permet dans l'énoncé de cette loi de comprendre pourquoi il y a une relation logarithmique entre l'intensité perçue d'un son et le logarithme de son intensité physique. Pourquoi, après tout, le lien ne serait-il pas direct, sans passer par un logarithme ?
En fait, on parlera de loi surtout si cette co-occurrence est vraiment constatée régulièrement, et même à chaque fois qu'on la teste. Si l'on constate au contraire que cette relation arrive de temps en temps, mais pas toujours, on aura déjà plus de mal à la qualifier de loi.
Nous venons de voir ce que pouvait-être la dépendance. Mais que serait alors l'indépendance ?
2.2. Indépendance de deux variables
L'indépendance de deux variables est le fait que, quelles que soient les valeurs prises par une variable, les valeurs prises par l'autre variable n'en sont pas affectées.
Par exemple, je regarde la tranche basse de revenus, et je trouve des individus de tous les âges, indifféremment. Si je regarde les deux autres tranches de revenus, je fais le même constat. Dans ces conditions, rien ne permet de penser qu'il existe un lien entre les variables. Prenons le problème dans l'autre sens et examinons pour une tranche d'âge donnée les revenus correspondants. Si j'observe que quelle que soit la tranche d'âge, la distribution des revenus est la même, alors j'ai toutes raisons de penser que les variables âge et revenu sont indépendantes.
Autrement dit, le constat de co-occurrence nous sert à poser des hypothèses générales sur le monde, ou des hypothèses diagnostiques sur les causes potentielles des problèmes. Le problème est alors de pouvoir tester ces hypothèses, ce qui passe par une approche plus systématique des co-occurrences.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte