Statistique descriptive
9. Prédire une variable numérique : la régression simple
9.1. La problématique de la régression
A. Prédire permet d'agir
Il existe deux mobiles fondamentaux pour acquérir de la connaissance. Le premier est le simple goût de la compréhension : on souhaite connaître parce que comprendre le monde procure directement un certain plaisir. C'est une seconde motivation de la connaissance que nous allons explorer ici : la connaissance nous permet d'acquérir un certain degré de contrôle sur le monde. Nous pouvons, grâce aux connaissances, augmenter la quantité de conséquences favorables qui risque de survenir suite à la situation actuelle, ou au contraire éviter les conséquences potentielles défavorables de la situation actuelle.
Dans le présent article, nous allons examiner comment utiliser les statistiques pour décrire le monde sous l'angle de la prédiction. Le problème est double :
produire les connaissances qui permettent de prédire
appliquer ces connaissances pour réaliser des prédictions
B. La prédiction s'appuie sur des indices
Pour réaliser la prédiction, nous avons besoin d'analyser l'état actuel du monde, puis d'établir une relation entre l'état actuel du monde et l'état futur du monde. Par exemple, je sais que si je lâche un objet maintenant, quelques instants après, il viendra s'écraser sur le sol. Les cas de prédiction intéressants ne sont pas aussi triviaux. Par exemple, si je suis médecin, connaissant une configuration de symptômes et de caractéristiques du patient, je vais m'intéresser à établir un pronostic, c'est-à-dire avoir une idée des chances de guérison du patient. En fonction de ce pronostic, et en fonction des moyens techniques disponibles, je vais pouvoir déclencher certaines actions. Même sans être médecin, nous faisons tous continuellement de la prédiction. Par exemple, si je suis au volant de ma voiture, je prends des indices sur le comportement des autres conducteurs autour de moi et j'en infère leur intention. Cette interprétation de l'intention des autres conducteurs me sert à prédire comment je dois piloter ma voiture pour me diriger dans le trafic efficacement et sans causer d'accident.
On peut aussi s'intéresser à la prédiction pour évaluer jusqu'à quel point il est possible d'utiliser une variable pour prédire une autre variable. Par exemple, imaginons un employeur qui fait passer des tests de QI lors des épreuves de sélection pour le recrutement. Il pourrait être tenté de recruter simplement les individus ayant le plus haut QI, sous l'hypothèse que ceux-ci sauront mieux s'adapter aux difficultés de leur vie professionnelle à venir. D'un autre côté, même si l'on sait que c'est globalement vrai, on sait aussi que la relation est loin d'être parfaite, car d'autres facteurs que les habiletés logico-mathématiques interviennent dans la réussite professionnelle. Selon les professions par exemple, la créativité, le contact humain, etc. peuvent constituer des prédicteurs de performance importants aussi que l'employeur pourrait donc être tenté de mobiliser dans son choix.
C. Formalisation du problème
Nous venons de voir que les connaissances qui pour réaliser des prédictions, il faut mettre en relation un état actuel du monde et un état futur du monde. Si nous réduisons le problème à sa plus simple expression, nous aurons donc une variable qui codera l'état actuel du monde et qui nous servira à prédire une autre variable qui codera l'état futur du monde.
Nous appellerons prédicteur la première variable. Dans la littérature, on trouve aussi les termes indice, ou encore, lorsque l'on suppose un lien causal entre l'état actuel et l'état futur, l'expression variable indépendante.
Nous appellerons variable prédite celle qui code l'état futur du monde. Dans la littérature, on trouve aussi le terme critère ou, en cas de relation causale, de variable dépendante.
Finalement, pour décrire l'ensemble de la question, il nous faut exprimer la relation qui existe entre la variable prédite, que nous noterons
Y, et la variable à prédire que nous noterons
X. On suppose alors qu'il existe une relation mathématique entre les deux, relation que l'on dénotera ici par la lettre grecque 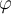 :
:
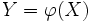
Ainsi posée, la question de la prédiction revient à chercher la nature de la relation 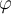 qui relie les variables X
et
Y, ou mathématiquement parlant, déterminer l'équation qui relie
X
et
Y.
qui relie les variables X
et
Y, ou mathématiquement parlant, déterminer l'équation qui relie
X
et
Y.
D. Principe de l'identification empirique de 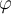
Pour étudier 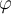 empiriquement, nous allons prendre des mesures de
X
et des mesures de
Y. Par exemple, nous demanderons leur âge à un échantillon de participants, et nous estimerons combien ils ont de rides sur le visage. À l’issue de ce recueil de données, nous disposons donc d’un ensemble de couples de données, un couple par sujet. Ensuite, nous appliquons des méthodes statistiques, graphiques, etc. pour essayer de comprendre quelle est la nature de la fonction
empiriquement, nous allons prendre des mesures de
X
et des mesures de
Y. Par exemple, nous demanderons leur âge à un échantillon de participants, et nous estimerons combien ils ont de rides sur le visage. À l’issue de ce recueil de données, nous disposons donc d’un ensemble de couples de données, un couple par sujet. Ensuite, nous appliquons des méthodes statistiques, graphiques, etc. pour essayer de comprendre quelle est la nature de la fonction 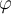 .
.
La régression linéaire, méthode qui nous occupe ici, se caractérise par le postulat que la relation φ peut être approchée par une fonction affine (c'est-à-dire par une droite que, par abus de langage, nous appelons souvent fonction linéaire) dont les propriétés sont connues, puis à évaluer à quel point cette fonction est capable de rendre compte des données observées. En d’autres termes, on part du principe qu’il existe une droite
F
dont l’équation est une bonne approximation de 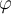 . Partant de cette hypothèse (et de quelques autres…) on applique des calculs mathématiques sur les données qui nous permettent d’évaluer les paramètres caractéristiques de F.
. Partant de cette hypothèse (et de quelques autres…) on applique des calculs mathématiques sur les données qui nous permettent d’évaluer les paramètres caractéristiques de F.
Dans un second temps, une fois F identifiée, on va évaluer à quel point
F
est ajustée aux données, c’est-à-dire à quel point
F
représente un bon modèle des données observées. Si cet ajustement est jugé satisfaisant, on pourra considérer, jusqu’à nouvel ordre, que la droite
F
est une bonne représentation de la fonction «vraie», j. Bien entendu, si  est trop différente d’une droite, on ne parviendra pas à trouver une droite
F
qui ressemble suffisamment à
est trop différente d’une droite, on ne parviendra pas à trouver une droite
F
qui ressemble suffisamment à 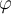 pour que l’on s’en satisfasse.
pour que l’on s’en satisfasse.
Dans une approche exploratoire pure, où l’on ignore a priori tout de φ, le simple fait d’appliquer cette méthode peut déjà constituer un premier apport de connaissances sur 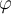 . Plus tard, on pourra vouloir améliorer notre capacité de prédiction, et il se peut que l’approximation linéaire ne soit plus acceptable : on aura alors besoin d’explorer les cas où
F
n’est pas une droite, mais une fonction plus complexe, ce qui, pour l’essentiel, on sort alors du cadre du présent cours.
. Plus tard, on pourra vouloir améliorer notre capacité de prédiction, et il se peut que l’approximation linéaire ne soit plus acceptable : on aura alors besoin d’explorer les cas où
F
n’est pas une droite, mais une fonction plus complexe, ce qui, pour l’essentiel, on sort alors du cadre du présent cours.
Nous allons maintenant passer à l'analyse détaillée de la méthode de régression.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte
Largeur de paragraphe