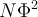Statistique : Tester l'association de variables
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L2 |
| Livre: | Statistique : Tester l'association de variables |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 3 février 2026, 08:08 |
Description
 Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales ( de Spearman,
de Spearman,  de Kendal), ou nominales (
de Kendal), ou nominales ( et
et  ). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
Table des matières
- 1. Tester la liaison entre deux variables
- 2. Régression linéaire simple : approche inférentielle
- 3. Contrôler l'effet d'une variable : Corrélation partielle
- 4. Régression linéaire multiple : coefficients multidimensionnels
- 5. Régression linéaire multiple : Ajustement du modèle
- 6. Régression linéaire multiple : La redondance des VI
- 7. Régression linéaire multiple : Ordre d'introduction des variables
- 7.1. Régression linéaire multiple : Ordre d'introduction des variables
- 7.2. Exemple d’Analyse par la méthode standard
- 7.3. La Méthode Statistique Ascendante
- 7.4. La Méthode Statistique Descendante
- 7.5. La Méthode Pas à Pas
- 7.6. Répartition entre VIs des parts de variance expliquée
- 7.7. Méthode d'introduction et Inférence statistique
- 7.8. Comparaison de deux ensembles de prédicteurs
- 7.9. Conclusion : Choix d’une méthode
- 8. Régression linéaire : Évaluer la qualité de la relation
- 9. Questionnaire d'auto-évaluation
1. Tester la liaison entre deux variables
Objectifs. Apprendre à tester la significativité de corrélations.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur les liaisons entre variables non numériques
- Introduction à la statistique inférentielle et notamment, l'approche intuitive
- de la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
Résumé. On commence par exposer comment tester la significativité d'une corrélation simple. On traite ensuite le cas d'une comparaison de deux corrélations indépendantes. On termine par l'exposé de la comparaison de deux corrélations dépendantes.
1.1. Tester une corrélation simple
Le coefficient de corrélation linéaire, r , peut varier entre -1 et +1. Une valeur nulle indique l’absence de relation linéaire, soit parce qu’il n’y a pas de relation du tout entre les variables considérées (cas de l'indépendance entre les deux variables), soit parce que la relation existe mais n’est pas linéaire (par exemple la relation est une parabole).
Le coefficient de corrélation est un nombre sans dimension (il n’a pas d’unité, contrairement à une longueur ou un poids).
Pour tester si une corrélation est significativement différente de 0, on peut calculer une version particulière de la statistique t :
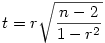
Cette statistique suit une loi de student à n -2 degrés de liberté. On peut donc la tester comme vu précédemment dans l'article sur le test du t .
Prenons un exemple numérique simple. Admettons que nous ayons calculé la corrélation entre deux variables mesurées sur un échantillon de 100 personnes et que nous ayons trouvé r =.305. Nous appliquons la formule et trouvons
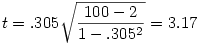
En accédant ensuite à la table du t ou bien à une formule de tableur équivalente, nous trouvons que pour (100-2)=98 degrés de liberté, la probabilité d'avoir un t au moins égal à 3,14 en valeur absolue est p =.002., donc notre r est significativement différent de 0, nous pouvons rejeter l'hypothèse nulle.
À noter : Statistica possède un petit outil qui calcule directement ces valeurs :
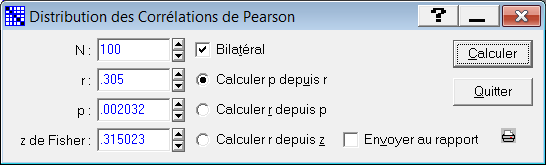
Notons que la corrélation est une variable signée dont la distribution est symétrique. Si nous avons une hypothèse sur le sens de la corrélation (donc le signe du r que nous devrions obtenir), et que la valeur observée de r est effectivement du signe attendu, nous pouvons calculer notre valeur p en unilatéral et donc diviser par deux le p obtenu par le test de Student. Ce qui ferait ici p =.001.
1.2. Comparer deux corrélations indépendantes
Supposons que nous disposions de deux corrélations r1 et r2. Par exemple, nous savons que chez les enfants la corrélation entre l'âge et le désir de fraises des bois est de .45 tandis que, chez les adultes, elle est de .30 (ce sont des chiffres complètement fantaisistes évidemment !). Nous voudrions savoir s'il est possible de dire statistiquement que la relation entre l'âge et le désir de manger des fraises des bois est plus forte chez les enfants que chez les adultes, comme le suggère l'écart entre les corrélations observées. Nous voulons donc savoir si la différence des deux corrélations observées peut être attribuée au hasard (hypothèse nulle) ou non.
Lorsqu'il s'agit de comparer deux corrélations, deux éléments doivent être pris en compte :
- On ne peut calculer pas simplement la différence de 2 corrélations comme on le faisait avec des moyennes.
- Il faut distinguer le cas où les deux corrélations ont été obtenues indépendamment l'une de l'autre du cas où ces corrélations sont elles-mêmes potentiellement corrélées (par exemple lorsqu'elles ont été obtenues sur les mêmes sujets ou qu'elles impliquent une variable commune). Seul le cas indépendant est traité ici.
2.1. La transformation de Fisher
Le coefficient de corrélation r de Pearson n'est pas une variable normalement distribuée. Sa distribution est bornée à +1 et -1 alors que la loi normale est définie sur l'ensemble des nombres réels. Et, surtout, les différences entre deux corrélations n'ont pas du tout la même valeur selon les régions de l'intervalle [-1; 1] concernées. Par exemple, une corrélation de.05 et.08, l'écart, .03, ne représente pas grand-chose. Au contraire, le même écart est considérable s'il différencie une corrélation de .96 et une corrélation de .99.
La solution à cette première difficulté est assez simple à mettre en œuvre du fait que l'on peut appliquer une correction aux valeurs de r, appelée transformation de Fisher (le même que celui de l'ANOVA). Après transformation de la valeur r en note r' , la distribution obtenue est à peu près normale. La transformation est la fonction dite "arctangente hyperbolique" (aussi notée "argtanh" en langage mathématique) dont la formule est
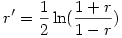
Autrement dit, on prend le logarithme népérien (fonction "ln" sous Excel) du rapport (1+ r ) / (1- r ), et on divise le résultat par 2. Notons que sous des tableurs comme Excel ou OpenOffice Calc, on peut directement obtenir la transformation au moyen de la fonction "atanh" qui prend la valeur à transformer comme argument. On peut aussi noter des limites à cette transformation car elle n'est pas définie dans les cas où r est exactement égal à +1 ou -1 car
- on ne peut pas faire une division par 0 (or, si r =1 alors 1- r = 0)
- la fonction logarithme n'est pas définie pour la valeur 0 (or, si r =-1, alors 1+ r = 0 et le rapport vaut 0 aussi).
On peut remarquer en outre, qu'après transformation, les valeurs ne sont plus contenues dans l'intervalle [-1; +1]. Par exemple, la transformée de .90 vaut à peu près 1.47 (après arrondi à la deuxième décimale) ce qui dépasse 1.
Si nous appliquons cette transformation à la première des deux corrélations vues plus haut, nous trouvons
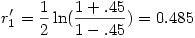
2.2. Comparer deux corrélations indépendantes
Le principe du test est très simple. Après transformation des corrélations r1 et r2 par la transformation de Fisher vue plus haut, on obtient r1' et r2'. Fisher a montré que l'on peut calculer de la façon suivante une statistique z qui suit une loi normale et que l'on peut tester en conséquence :
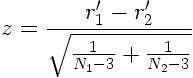
on obtient alors facilement la valeur p associée à cette note z .
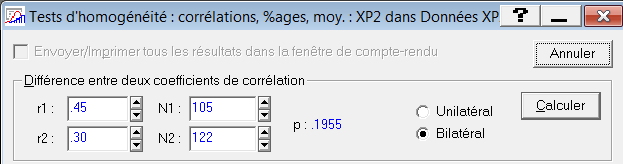
Si nous reprenons notre exemple numérique (comparer r1 =.45 et r2 =.30), et en supposons que nous avons obtenu nos corrélations auprès de 105 enfants et 122 adultes, on voit d'abord que la transformation de Fisher, après arrondi, donne r1 '=.485 et r2 '=.310 et, alors, il vient
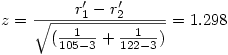
En prenant une table du z ou en utilisant un tableur, on trouve que la probabilité que z atteigne au moins cette valeur si l'hypothèse nulle est vraie est p =.194, ce qui n'est pas significatif : les deux corrélations ne sont significativement pas différentes.
À noter : Statistica possède une fonction de comparaison des corrélations, qui donne un résultat légèrement différent à partir de la troisième décimale :
1.3. Comparer deux corrélations dépendantes
Cette section est adaptée à partir d'un article de Steiger (1980) et en reprend les notations.
Il y a trois cas dans lesquels les corrélations à comparer ne sont pas indépendantes et où le traitement s'avère plus complexe :
- lorsque les corrélations ont été obtenues sur les mêmes sujets
- lorsque les corrélations partagent une variable en commun
- lorsque l'on teste la même corrélation à des moments différents
Nous ne traitons ici que du cas n°2 : Nous avons deux corrélations obtenues avec N sujets. Avec Steiger (1980), appelons j la variable commune, h et k les deux autres. Nos corrélations sont rjk et rjh .
1°) Il nous faut évaluer le degré de dépendance entre ces deux corrélations, et cette information nous est fournie par le calcul de la troisième corrélation, rhk. À partir de ce moment, on dispose de trois corrélations.
2°) On applique la transformation de Fisher aux deux premières corrélations (rappelons que c’est la fonction arctangente hyperbolique), ce qui donne deux corrélations transformées rjk' et rjh' avec
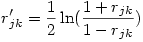
et
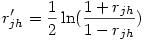
3°) Puisque nous testons l'hypothèse nulle que rjk = rjh, on peut avantageusement remplacer chacune des deux corrélations observées par la moyenne des deux et utiliser cette dernière dans les équations suivantes :
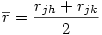
ou encore
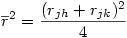
4°) On calcule ensuite
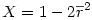
5°) On calcule alors un écart-type groupé Shk
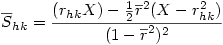
6°) Finalement la variable
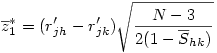
suit une loi normale classique qu'il suffit de tester comme toute valeur z.
1.4. Tester la liaison entre deux variables ordinales
4.1.  (rho) de Spearman
(rho) de Spearman
Rappelons que le  de Spearman
(voir la section A de l'article Liaisons entre deux variables ordinales) consiste à calculer un coefficient de coefficient de corrélation classique (r
de Pearson) mais sur des données qui ont été préalablement transformées en rangs.
de Spearman
(voir la section A de l'article Liaisons entre deux variables ordinales) consiste à calculer un coefficient de coefficient de corrélation classique (r
de Pearson) mais sur des données qui ont été préalablement transformées en rangs.
De ce fait, au plan inférentiel, il se teste exactement comme la corrélation simple que nous avons vue en première page du présent article.
4.1.2. Tau de Kendall
Lorsque nous avons deux variables ordinales à corréler, disons V1 et V2,nous avons deux faits deux classements. Nous avons vu dans le cours de L1 (voir la section B de l'article Liaisons entre deux variables ordinales) que le test de Kendall consiste d'abord à trier les sujets selon les valeurs croissantes de la première variable, donc à faire en sorte que quelles que soient deux observations, la valeur mesurée sur V1 de l'observation la mieux classée sera plus grande que la valeur mesurée sur V1 de l'observation la moins bien classée. On considère ensuite les mesures prises sur V2, mais toujours dans l'ordre induit par V1. On examine alors toutes les paires possibles d'observations, puis on compte les paires de données concordantes (c'est-à-dire où, comme pour la première variable, le premier nombre sur V2 est plus petit que le second nombre sur V2) et celles qui sont discordantes (celles où, contrairement à la première variable, le premier nombre sur V2 est plus grand que le secondnombre sur V2). On obtient dond deux nombres, n c le nombre de paires concordantes et n d le nombre de paires discordantes. On divise alors la différence des deux par le nombre total de paires possibles, ce qui fait :
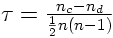
Sous l'hypothèse nulle,  est nul et sa variance est
est nul et sa variance est
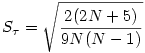
Le  est distribué à peu près normalement dès que
N
>9 et donc on peut tester la valeur z
est distribué à peu près normalement dès que
N
>9 et donc on peut tester la valeur z
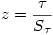
en utilisant la loi normale, comme nous l'avons fait jusqu'ici. En reprenant l'exemple vu dans le cours de L1, nous avions Tau=0.067 pour N =6 (pour l'exemple, glissons sur le fait que N n'atteint pas 9 !).
et donc z=0.067/0.3549=0.189, ce qui n'est évidemment pas significatif.
1.5. Liaison entre deux variables nominales
A.  d'indépendance (ou "Khi-deux", ou "Chi-2").
d'indépendance (ou "Khi-deux", ou "Chi-2").
Le  s'applique lorsque l'on dispose d'une table de contingence, c'est-à-dire lorsque l'on répartit les effectifs dans un tableau de
L
lignes et
C
colonnes. Par exemple, si l'on croise la variable sexe (Hommes, Femmes), avec une variable Tabagie (Non fumeur, Fumeur occasionnel, fumeur régulier), nous obtenons un tableau dans lequel chaque individu sera compté dans une seule case.
s'applique lorsque l'on dispose d'une table de contingence, c'est-à-dire lorsque l'on répartit les effectifs dans un tableau de
L
lignes et
C
colonnes. Par exemple, si l'on croise la variable sexe (Hommes, Femmes), avec une variable Tabagie (Non fumeur, Fumeur occasionnel, fumeur régulier), nous obtenons un tableau dans lequel chaque individu sera compté dans une seule case.
Nous avons vu dans le cours de L1 (section A de l'article Liaisons entre variables nominales) comment
calculer un . Nous renvoyons donc à cet article pour le détail des calculs de la valeur du
. Nous renvoyons donc à cet article pour le détail des calculs de la valeur du  proprement dite.
proprement dite.
Une fois cette valeur obtenue, on obtient le nombre de degrés de liberté tout simplement par la formule suivante :
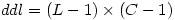
C'est le (nombre de lignes - 1) multiplié par le (nombre de colonnes - 1). Dans notre exemple précédent, cela donne (2-1)(3-1)=2.
est connue et l'on peut donc directement trouver la valeur p associée en entrant dans une table (ou avec un tableur) avec la valeur et le bon nombre de degrés de liberté.Attention toutefois au fait que la distribution du Chi-deux n'est pas symétrique et donc qu'il n'est pas légitime de travailler en unilatéral.
Précaution n°2 : la totalité des effectifs doit être incluse dans le test sous peine d'avoir des résultats biaisés. Par ailleurs, que les variables s'avèrent finalement indépendantes ou non, le test n'est valide que si les mesures sont indépendantes, ce qui n'est pas le cas si un même sujet produit des données dans plusieurs cases du tableau. Finalement, la précaution n°2 dans son ensemble se résout si l'on prend soin de vérifier que le nombre de sujets pris en compte dans l'étude est bien la somme totale des effectifs du tableau, ni plus ni moins.
B. L'indice  (phi)
(phi)
Une fois que l'on sait réaliser le test du Chi-deux, le test du Phi est presque immédiat car puisque
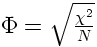
Ce qui revient à dire que
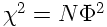
2. Régression linéaire simple : approche inférentielle
Objectifs. Apprendre à réaliser concrètement une régression linéaire avec un logiciel de statistique.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur les liaisons entre variables non numériques
- Introduction à la statistique inférentielle et notamment, l'approche intuitive
- de la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables
Résumé. L'article part du principe que l'étudiant dispose d'un logiciel de statistique pour réaliser les calculs. On présente les traitements à réaliser et comment interpréter les principales données produites par les logiciels.
2.1. Analyses préalables
L’intérêt de ces analyses est surtout de repérer si les postulats de base de la régression linéaire sont remplis (comme la linéarité de la relation entre la VI et la VD) et si certaines valeurs ne se distinguent pas franchement du reste. Cela peut arriver notamment en cas d’erreur de saisie, ou encore un sujet peut n’avoir pas compris (ou pas voulu suivre) la consigne et produit des résultats tout à fait hors norme, et même parfois tout à fait incohérents.
À titre d'exemple, au cours de l'article, nous examinerons l’influence d’une variable nommée F02J sur une seconde variable nommée DVP. Pour l’exemple, peu importe ici ce que ces variables représentent.
1.1. Variables dépendante et indépendante
La première étape d'une régression consiste à entrer les variables à prendre en compte, en distinguant les variables dépendantes (variables prédites) et indépendantes (prédicteurs).
Il y a plusieurs variables indépendantes lorsqu’il y a plusieurs prédicteurs. Par exemple, on veut tester l’hypothèse que la réussite universitaire est prédite par une fonction linéaire (1) du nombre d’heures passées à travailler ET (2) du QI. On parle alors de « régression multiple ». Nous examinerons dans un autre article les problèmes qu’ajoute la régression multiple par rapport à la régression simple. Dans cette dernière, nous n'avons qu'une variable indépendante.
Simple ou multiple, la régression linéaire ne s’applique qu’à une seule variable prédite. Toutefois, il est possible dans certains logiciels de saisir plusieurs variables dépendantes. Celles-ci font alors chacune l’objet d’une analyse en régression indépendante des autres.
La régression simple consiste à produire l’équation d’une droite de la forme Y = aX + b, droite qui résume le mieux possible le nuage de points. D’une certaine manière, on peut dire que les valeurs de Y sont prédites par la combinaison d’une constante et d’une autre variable, X.
1.2. Analyse descriptive des variables considérées
On commence généralement par observer comment se présentent les variables qui vont entrer dans la régression.
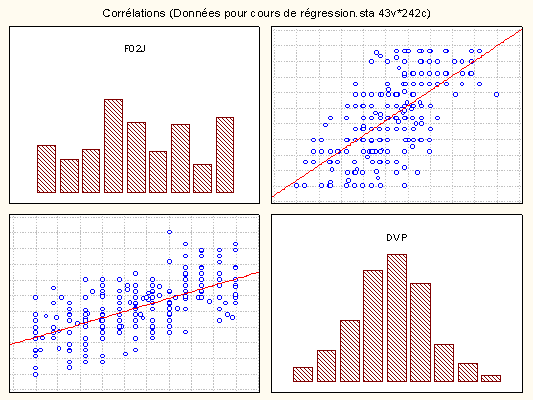
Ici, on voit que la variable à prédire (DVP) se distribue normalement alors que la variable prédictrice (F02J) est plutôt uniformément distribuée.
En dépit de ce qui se dit parfois, cela n'a aucune importance dans le cas de la régression : pour permettre l'inférence statistique, seuls les résidus de la régression doivent être normalement distribués pour que l'on puisse considérer que le modèle est satisfaisant !
2.2. La régression proprement dite
Attention : là où la version française de certaines versions de SPSS (e.g., SPSS 18) indique « valeur prédite »dans les résultats, il s’agit en fait d’une erreur de traduction. Il faut lire« prédicteur » comme l’indique la version anglaise de SPSS qui mentionne « Predictors ».
Sous SPSS, nous obtenons les résultats suivants (Il manque ici un premier tableau qui n’aura d’intérêt que lorsque nous verrons la régression multiple) :



Sous Statistica, la même analyse nous donne les résultats suivants :

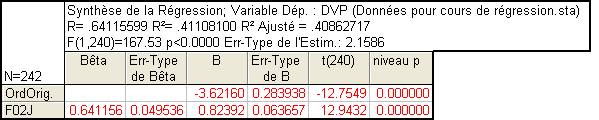
Aux détails de mise en forme près, ces résultats se ressemblent furieusement… ce qui est plutôt rassurant!
Expliquons maintenant comment lire ces résultats.
Si nous prenons les trois tableaux de SPSS, les deux premiers concernent l’ajustement global du modèle aux données, le troisième décrit plus précisément la relation entre le ou les prédicteurs (ici le prédicteur) et la variable dépendante.
2.3. Récapitulatif du modèle
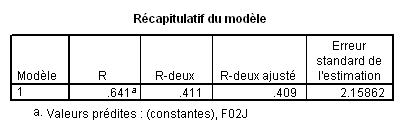
R (ou « R multiple » dans Statistica) : Il s’agit de la corrélation que l’on peut constater entre les données prédites par la droite calculée et les données réellement observées.
R traduit donc l’ajustement du modèle aux données et doit se rapprocher le plus possible de 1.
R -deux ou R² : c’est simplement le carré de R . Le carré d’une corrélation traduit la part de la variance du nuage de points expliquée par la droite de régression. Ici, la droite de régression est le modèle et R ² traduit donc la part de variance expliquée par le modèle, en l’occurrence 41,1%.
On peut aussi calculer R² directement comme part de variance expliquée par le modèle, et prendre sa racine carrée pour calculer R.
R -deux ajusté : Dans le cas général (régression multiple), c’est une valeur de R corrigée, essentiellement pour réduire un biais lié au fait que chaque prédicteur supposé peut expliquer une partie du nuage de points par le seul fait du hasard. Dans le cas de la régression simple, si n est le nombre d’observations, on a
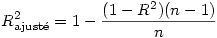
Lorsque l’on rapporte la part de variance expliquée par le modèle, mieux vaut rapporter la valeur du R ² ajusté.
Ce dernier tend vers R ² lorsque le nombre de prédicteurs est petit et lorsque le nombre d’observations devient grand. Dans SPSS et Statistica, le R²ajusté est calculé par la formule précédente mais il en existe d’autres, pour le cas où l’échantillon est petit.
Erreur standard de l’estimation : indice de dispersion des valeurs prédites. Il est égal à l’écart type des valeurs prédites divisé par la racine carrée du nombre d’observations. On utilise l’erreur standard plutôt que l’écart-type afin de pouvoir comparer des modèles ne comportant pas le même nombre d’observations.
2.4. Tableau d'ANOVA de la régression

Ce tableau d'ANOVA rend compte de l’analyse de la variance totale des données, en la partitionnant en une partie expliquée par le modèle (Régression) et une partie non expliquée (Résidu).
ddl : nombre de degrés de liberté associés à la source de variance. Pour la régression, il est égal au nombre de prédicteurs (constante incluse) moins 1. Donc toujours 1 pour la régression d'une régression simple.
Somme des carrés : Il s’agit de la somme des carrés des écarts à un point de référence Σ(yi -refi )². Au vu de la définition de la variance, on voit qu’une variance d'échantillon n’est qu’une somme des carrés divisée par le nombre d’observations qui la concernent, moins une, (voir l'article consacré à la somme des carrés dans l'article sur l'ANOVA).
Pour la ligne Total, la référence est constante, c’est la moyenne my du nuage de points.
Pour la ligne « Résidu », la référence est la valeur prédite par le modèle pour chaque observation.
Pour la ligne régression, la référence est la différence entre la valeur prédite parle modèle et la valeur moyenne my. La somme des carrés de la régression représente donc l’amélioration de prédiction qu’apporte le fait d’utiliser la valeur prédite par le modèle plutôt que la valeur moyenne de l'ensemble du nuage de points.
Accessoirement, on retrouve R ² en divisant la somme des carrés de la régression par la somme des carrés totale, ce qui est normal puisque R² est la part de variance expliquée par le modèle.
Carré moyen : Somme des carrés divisée par le nombre de degrés de liberté.
F : Statistique F de Fisher-Snedecor, obtenue en divisant le carré moyen de la régression par le carré moyen des résidus.
Signification : la valeur classique du p. Sans grand intérêt ici car quasiment toujours significatif dans ces analyses, notamment du fait que le modèle inclut une constante.
2.5. Les coefficients de régression

Comme son nom l’indique, ce tableau donne les paramètres de la droite de régression.
Les coefficients non standardisés : Ce sont les valeurs brutes des constantes, appelés les « B ».
Par exemple, à partir du tableau ci-dessus, on voit que la droite de régression peut s’écrire :
Y = .824* X – 3.622
où Y représente la variable dépendante DVP et X représente la variable indépendante F02J.
Autrement dit, un accroissement d’une unité sur la VI se traduit par un accroissement de B unités sur la VD, sauf dans le cas de la ligne "constante" qui représente la valeur de la VD lorsque la VI est nulle.
Les coefficients standardisés : Valeurs standardisées des constantes, appelés les « Bêtas ».
Les coefficients standardisés expriment le coefficient de régression qu’il faut appliquer aux scores standardisés de la VI (les « z scores » de la VI, c’est-à-dire les valeurs centrées réduites) pour prédire les z scores de la VD : Un bêta de 0.5 signifie qu’un accroissement d’un écart-type de la VI se traduit par un accroissement d’un demi écart-type de la VD. Nous en traiterons lorsque nous aborderons la régression multiple.
Erreur standard : sert à calculer la valeur de t en vue de tester si le coefficient (et donc la prédiction) est significativement différent de 0. L'erreur standard sert aussi à calculer des intervalles de confiance des coefficients (c'est-à-dire la probabilité que la "valeur vraie" du coefficient soit comprise dans un intervalle défini par la valeur B plus ou moins (le plus souvent) 2 erreurs standard.
t et signification : valeur du t de Student associé au coefficient et probabilité bilatérale d’obtenir une telle valeur de t si l’hypothèse nulle est vraie.
Sert à calculer si la valeur du coefficient est significativement différente de 0, c’est-à-dire si le prédicteur considéré est véritablement capable de prédire les variations de la variable dépendante. Pour plus de détails sur l'utilisation de la statistique t, voir l'article sur le test t.
Ici, il n’y a aucun problème à rejeter l’hypothèse nulle, c’est-à-dire à accepter que la variable F02J prédit de façon significative les variations de la variable dépendante.
À noter : lorsque l’on a une hypothèse théorique sur le sens de la prédiction, et que le signe de B est dans la direction théoriquement prévue, onpeut utiliser un test unilatéral, c’est-à-dire diviser la valeur affichée de p par 2 avant de considérer le rejet ou non de l’hypothèse nulle.
2.6. Enregistrement des valeurs prédites et résidus
Aussi bien R que SPSS ou Statistica permettent d’enregistrer les valeurs prédites et les résidus, observation par observation, ainsi que d’autres informations pouvant être utiles mais que nous ne détaillerons pas ici. Voici un exemple dans Statistica :
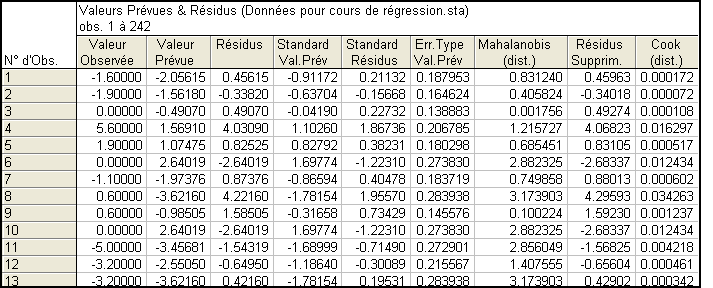
On peut vérifier que, observation par observation, on a bien
Valeur observée = valeur prédite +résidu.
3. Contrôler l'effet d'une variable : Corrélation partielle
Objectifs. Comprendre la nature d'une corrélation partielle.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur l'Approche intuitive
- Cours de L1 sur la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables : descriptive L1 / Inférentielle L2
- Corrélation
- Régression simple (L1)
Résumé. On commence par exposer l'utilité de la notion de corrélation partielle puis on en donne le principe général. On détaille ensuite le fonctionnement sous-jacent à la technique sur un exemple.
3.1. Principe et méthode
1.1. Pourquoi faire une corrélation partielle
Il arrive que l'on constate une relation positive entre deux variables, mais que cette relation paraisse curieuse. De fait, il arrive parfois qu'une corrélation soit illusoire : la relation existe statistiquement mais ne traduit pas un lien de cause à effet entre les deux variables. Pour illustrer cela, prenons un exemple caricatural mais parlant :
Supposons que l'on mesure la couleur des dents de participants de 50 ans, mesurée sur une échelle de 0 à 10, où 0 est blanc pur et 10 est noir pur. Supposons que l'on mesure par ailleurs l'espérance de vie en bonne santé de ces participants. Vingt ans après, on s'aperçoit que l'espérance de vie en bonne santé est beaucoup plus faible chez ceux qui ont les dents jaunes. L'espérance de vie ne peut pas causer les dents jaunes. Une analyse superficielle pourrait faire penser qu'avoir des dents sombres réduit l'espérance de vie. Cela paraît toutefois douteux, car on ne voit pas pourquoi la couleur des dents affecterait sensiblement la santé. Avec un peu de réflexion, on peut être amené à penser qu'une troisième variable cause à la fois le jaunissement des dents et une réduction d'espérance de vie en bonne santé. Et effectivement, une telle variable existe, à savoir le tabac qui d'une part jaunit les dents, et d'autre part provoque cancers, maladies cardiovasculaires, AVC, etc. La question du chercheur devient alors, "comment s'assurer que le tabac est bien le vecteur de la relation entre couleur des dents et réduction de l'espérance de vie en bonne santé ?". C'est ce que va lui permettre de tester la corrélation partielle.
1.2. Méthode de la corrélation partielle
Le principe de la corrélation partielle est de calculer une corrélation de la même façon que d'habitude, mais après avoir retiré de chacune des deux variables l'effet de la troisième variable, celle que l'on cherche à contrôler.
Pour retirer cet effet, nous allons utiliser une propriété essentielle de la régression linéaire : la régression permet de distinguer, pour chaque individu, une part de la note de la VD attribuable au facteur, et une part résiduelle, attribuable soit à des erreurs de mesure, soit à l'intervention d'autres facteurs, inconnus. Or justement ce résidu nous intéresse ici, car il représente la part de la VD qui n'est pas déterminée le facteur caché (linéairement en tout cas).
Nous ne revenons pas ici sur le détail de la technique de régression. Il nous suffira de rappeler que lorsque l'on fait une régression, par exemple avec SPSS, Statistica ou un autre logiciel de statistiques, il est généralement possible d'enregistrer séparément les résidus et la partie prédite de chaque note : La partie prédite correspond à la part expliquée par le facteur et le résidu correspond à la part qui n'est pas expliquée par le facteur.
Techniquement, la régression permet de déterminer l'équation d'une droite de régression qui résume au mieux le nuage de points entre le facteur et la variable prédite. Cette droite est caractérisée par une équation 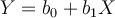 , où
Y
est la valeur de la VD et
X
la valeur de la VI (le prédicteur),
b0
et
b1
sont des constantes. Pour chaque sujet on a donc une valeur du prédicteur, et connaissant la valeur des paramètres, on peut calculer la valeur prédite correspondante. On note "
Y
chapeau" la valeur prédite de la VD :
, où
Y
est la valeur de la VD et
X
la valeur de la VI (le prédicteur),
b0
et
b1
sont des constantes. Pour chaque sujet on a donc une valeur du prédicteur, et connaissant la valeur des paramètres, on peut calculer la valeur prédite correspondante. On note "
Y
chapeau" la valeur prédite de la VD :
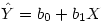
Dans la pratique, la valeur prédite est presque toujours différente de la valeur observée. On peut donc écrire que la valeur observée de la VD, Y, est égale à la valeur prédite plus un résidu :
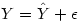
Nous avons vu dans le cours de L1 comment obtenir les coefficients b0 et b1. Donc, on peut calculer le résidu par différence des deux équations précédentes :
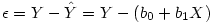
Si l'on calcule les résidus, sur Y et sur X, on obtient deux nouvelles variables dont aucune des deux ne dépend de Z, le facteur que l'on veut contrôler. On voit alors l'intérêt de passer par l'intermédiaire de la régression : pour obtenir la corrélation partielle qui retire l'effet du facteur que l'on suppose à l'origine de la corrélation, il suffit de calculer la corrélation entre les résidus de deux régressions, l'une où le facteur prédit la VD1, l'autre où le facteur prédit la VD2.
3.2. Un exemple détaillé
2.1. Les données de l'exemple
Pour cet exemple, nous avons généré un jeu de pseudo données dans lesquelles deux "Variables dépendantes", VD1 et VD2, ont été créées par ajout d'une valeur aléatoire à chacune des valeurs d'une "Variable indépendante". Voici les données.
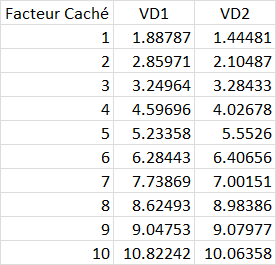
Par exemple pour le premier "sujet", le facteur caché est 1 et la VD 1 a été créée en ajoutant 0.88787 tandis que la VD2 était créée en ajoutant 0.44481.
2.2. La matrice de corrélations brutes
La matrice de corrélations que l'on obtient à partir de ces trois variables est la suivante :
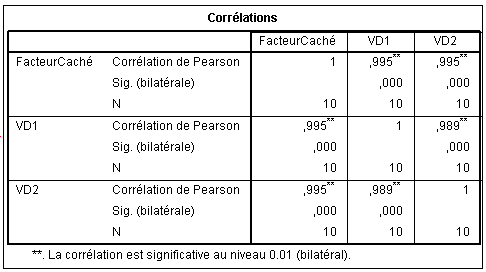
On voit que la relation entre la VD1 et la VD2 sont extrêmement fortes : .995 et très significatives évidemment malgré le petit effectif. Mais on voit aussi, et cela n'a rien d'étonnant, que le facteur caché est aussi très corrélé aux deux VD. Nous allons donc émettre l'hypothèse (vraie bien sûr puisqu'on a construit les données ainsi !) que le facteur caché explique en fait la corrélation entre VD1 et VD2. Mais comment nous en assurer ? Il faut faire une corrélation partielle.
Nous commençons par détailler le processus pour assurer la compréhension, mais toute cette opération est faisable en deux ou trois clics dans un logiciel comme SPSS.
Commençons par réaliser les deux régressions.
2.3. Les deux régressions simples
2.3.1. Régression de VD1 sur le facteur caché
Nous ne nous intéressons pas du tout ici à savoir si cette régression est significative car en réalité seul nous intéresse d'obtenir les valeurs des résidus.
Pour la compréhension, nous montrerons tout de même la reconstruction de l'équation de la droite de régression, donnés par le tableau des coefficients :
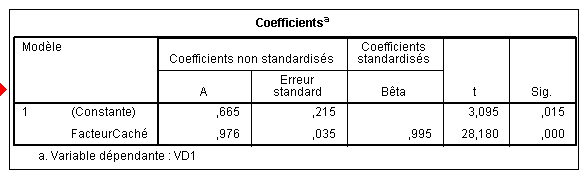
Nous obtenons ces coefficients dans la colonne A : b0 vaut .665 et b1, le coefficient attaché au facteur caché vaut .976. d'où l'équation
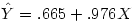
On peut enregistrer directement les prédictions et les résidus via une option de la régression et nous les obtenons directement dans les colonnes renommées ici Prévision1 et Résidu1:
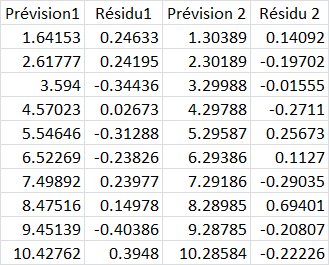
On peut facilement vérifier sur le sujet 1 que 1.64153+0.24633=1.88786 ce qui aux arrondis près correspond à notre VD observée 1.88787.
Et l'on vérifie aussi, toujours aux arrondis près (car la vraie valeur du coefficient b1 par exemple est 0.976231762090997), que la valeur prédite correspond à l'équation. En effet, la valeur du prédicteur étant 1 pour ce sujet, on a .665+1*.976=1.64153.
Le même raisonnement s'applique pour les coefficients, valeurs prédites et résiduelles de la régression 2 :
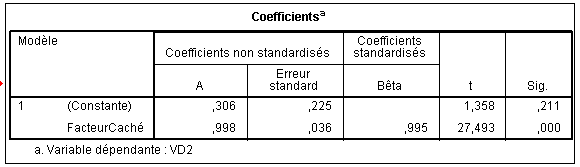
Ici, b0 vaut .306 et b1 , le coefficient attaché au facteur caché vaut .998. d'où l'équation
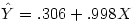
2.3. La corrélation partielle
Finalement, nous pouvons facilement calculer la corrélation entre les deux colonnes de résidus. Par exemple sous Excel avec la fonction "Pearson " et nous trouvons -.11013841. Il ne nous reste qu'à tester cette corrélation comme nous l'avons vu dans l'article sur le test des corrélations à un détail près : il y a ici n -3 degrés de libertés et non n -2 comme dans une corrélation normale. Nous trouvons alors p =.77788363.
En fait, SPSS nous permet de sortir directement la matrice où l'effet de la variable de contrôle, que nous avons nommée "FacteurCaché", sur la corrélation entre VD1 et VD2 est contrôlé :
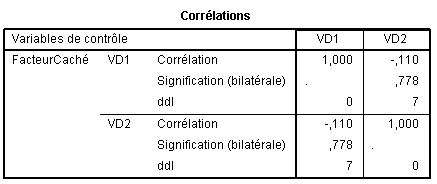
Ce qui correspond bien à nos calculs. Nous voyons à ce moment que la corrélation entre VD1 et VD2, une fois retiré l'effet du facteur caché s'effondre à -.110 et n'est plus du tout significative, comme on pouvait s'y attendre malgré la corrélation initiale apparemment extrêmement forte.
4. Régression linéaire multiple : coefficients multidimensionnels
Objectifs. Apprendre à réaliser concrètement une régression linéaire multiple avec un logiciel de statistique. Introduire en L2 les premiers problèmes que soulève la présence simultanée de plusieurs prédicteurs dans une analyse.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur l'Approche intuitive
- Cours de L1 sur la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables : descriptive L1 / Inférentielle L2
- Corrélation
- Régression simple (L1)
Résumé. L'article part du principe que l'étudiant dispose d'un logiciel de statistique pour réaliser les calculs. On présente les traitements à réaliser et comment interpréter les principales données produites par les logiciels.
4.1. Ajustement multilinéaire d'un nuage de points
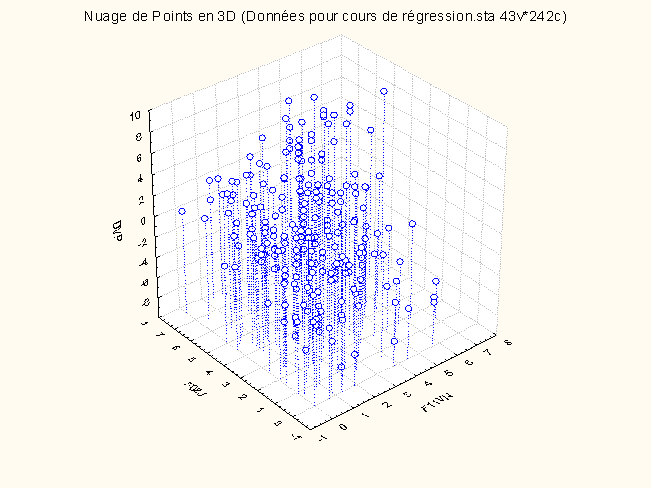
1.1. Nuage de points multidimensionnel
Lorsque nous voulons régresser une VD sur k prédicteurs, nous ne cherchons plus seulement à modéliser un nuage de points dans un plan (2 dimensions) mais plus généralement dans un espace à k dimensions. Par exemple, si nous ajoutons un nouveau prédicteur à la régression des articles précédents, F11VN, nous cherchons en fait à modéliser un nuage de points dans un espace à trois dimensions :
1.2. Ajustement multilinéaire
Le fait d’être dans un espace à k dimensions ne change pratiquement rien au fond des concepts vus plus haut. Ainsi, imaginons un espace à 3 dimensions, c'est-à-dire où chaque point est défini par sa valeur sur chacune des trois variables X0 , X1 et Y , l’équation de la droite qui s'ajustera le mieux au nuage de points dans cet espace s’écrira
Y = b0 + b1 X1 + b2 X2
Nous n’avons plus une « droite de régression » mais un « plan de régression » :
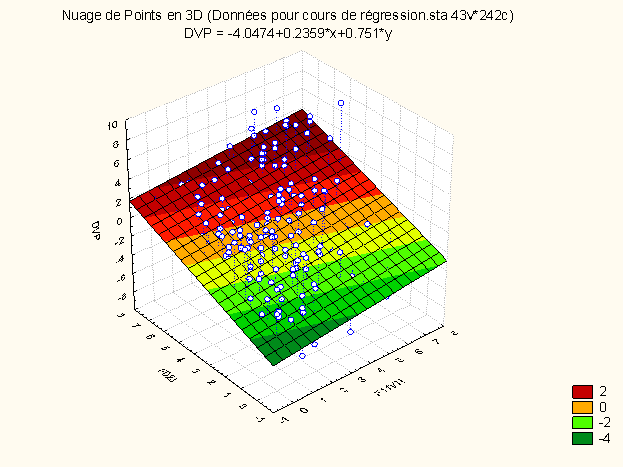
Ou encore plus généralement, dans un espace à k dimensions, nous avons un « hyperplan de régression » :
Y = b0 + b1 X1 + b2 X2 + … + bk Xk
Cela devient franchement difficile à se représenter mentalement, mais cela n’a en pratique qu’une importance mineure, car les principes restent les mêmes.
4.2. Les coefficients de la régression multiple
Prenons l’exemple d’une régression à deux prédicteurs : DVP est la VD, F11VN et F02J sont les prédicteurs.
Nous obtenons :
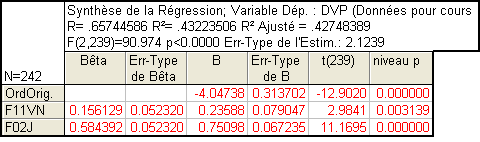
Ce tableau ressemble très fortement à celui de la régression simple mais appelle quelques commentaires.
Les B : Comme dans la régression simple, les coefficients B de la régression multilinéaire correspondent aux constantes qui définissent le poids de chaque prédicteur dans l’équation de régression.
L’équation ici est donc DVP = -4.048 + 0.236*F11VN + 0.751*F02J.
C’est l’équation du plan dans la figure vue plus haut.
Les bêtas : Comme dans la régression simple, ce sont les coefficients standardisés. On passe des β aux b par la relation
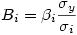
où σ y et σ i représentent les écarts-types de la VD et de la VI, respectivement.
On passe des b aux β par la relation inverse
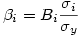
Attention :Il s’agit des écarts-types de la population et non des écarts-types corrigés (ce qui explique qu’on les note ici σ et non s).
5. Régression linéaire multiple : Ajustement du modèle
Objectifs. Apprendre à réaliser concrètement une régression linéaire multiple avec un logiciel de statistique. Présentation de l'évaluation de la qualité globale du modèle obtenu.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur l'Approche intuitive
- Cours de L1 sur la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables : descriptive L1 / Inférentielle L2
- Régression simple approche descriptive (L1)
- Régression simple : approche inférentielle (L2)
Résumé. L'article part du principe que l'étudiant dispose d'un logiciel de statistique pour réaliser les calculs. On présente les traitements à réaliser et comment interpréter les principales données produites par les logiciels.
Le R² : Dans une régression multilinéaire, le R²fournit la part de variance expliquée par l’ensemble des prédicteurs :
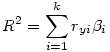
β i est le bêta du i ème prédicteur et ryi le coefficient de corrélation entre ce prédicteur et la VD.
Dans l’exemple précédent (F11VN et F02J qui prédisent DVP), si nous prenons la matrice de corrélations des variables impliquées :

et que nous appliquons les bêtas obtenus dans la régression précédente
Nous obtenons R² = (.369*0.156)+ (.641*0.584)= 0.432, ce qui est bien le R ² annoncé dans cette régression.
R-deux ajusté : Comme nous l’avons dit à propos de la régression simple, c’est une valeur de R corrigée pour réduire un biais lié au fait que chaque prédicteur supposé peut expliquer une partie du nuage de points par le seul fait du hasard. Or, ce biais augmente avec le nombre de prédicteurs. Si n est le nombre d’observations et k le nombre de prédicteurs (sans compter la constante),
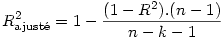
6. Régression linéaire multiple : La redondance des VI
Objectifs. Apprendre à réaliser concrètement une régression linéaire multiple avec un logiciel de statistique : prendre en compte la question de la multicolinéarité.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur l'Approche intuitive
- Cours de L1 sur la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables : descriptive L1 / Inférentielle L2
- Régression simple approche descriptive (L1)
- Régression simple : approche inférentielle (L2)
Résumé. L'article part du principe que l'étudiant dispose d'un logiciel de statistique pour réaliser les calculs. On présente les traitements à réaliser et comment interpréter les principales données produites par les logiciels.
6.1. Colinéarité et variance expliquée
1.1. La question de la redondance
Idéalement, les VI devraient ajouter chacune un aspect différent des variations de la VD, faute de quoi l’équation comprend des termes redondants. Dans les méthodes linéaires, le contraire de la redondance entre VI est l’orthogonalité des VIs :
L’orthogonalité est le fait que deux variables soient linéairement indépendantes, c'est-à-dire que la corrélation entre deux variables orthogonales est 0. Le terme même d’orthogonalité provient de l’interprétation géométrique de la corrélation linéaire simple. On peut montrer que le cosinus de l’angle formé par les deux droites de régression d’un nuage de points à deux dimensions (cas vu plus haut) est en relation avec le coefficient de corrélation entre les deux variables. Si les deux variables sont indépendantes,l’angle que font les droites de régression est de 90° (les variables sont alors dites orthogonales), le cosinus de l'angle est alors nul et le coefficient de corrélation aussi. Inversement, si deux variables sont parfaitement et positivement liées, l’angle est nul et le coefficient de corrélation vaut 1. Ou bien si les variables sont parfaitement et négativement liées, l’angle est de 180° et le coefficient de corrélation vaut -1.
Ce qu'il faut surtout retenir c'est que si les prédicteurs (les VIs) ne sont pas des variables indépendantes (ce qui est très souvent le cas), cela peut introduire des biais dans les analyses.
1.2 Définition de la colinéarité
Géométriquement, la colinéarité est le contraire de l’orthogonalité, au sens où les deux droites de régression forment un angle non droit (le mot même de "co"-"linéarité" suggère le partage d'un certain alignement). Deux variables sont dites colinéaires lorsqu’elles sont linéairement dépendantes l’une de l’autre. Concrètement, on pourra dire que deux variables sont colinéaires dès l’instant où la corrélation entre les deux est statistiquement significative.
1.3 Colinéarité et additivité des parts de variance expliquées
La conséquence de la colinéarité entre deux VIs est que les effets respectifs de chacun de ces deux prédicteurs ne se cumulent pas simplement. En effet, si deux variables sont colinéaires, cela implique qu’elles partagent une partie de leur variance. Plus précisément, on peut distinguer une variance propre à la VI1, une variance propre à la VI2, et une variance commune aux deux. Comme toujours, la part de variance partagée par deux variables est égale au carré de leur corrélation linéaire.
Si l’on ajoutait simplement l’effet de la VI1 et celui de la VI2, sans autre forme de procès, on compterait deux fois l’effet de la variance commune aux deux et une seule fois l’effet de la variance propre à chaque VI. Prenons l’exemple du nuage de points précédent.
Nous avons vu plus haut que la régression simple de DVP par F02J explique environ 41% de la variance de cette dernière.
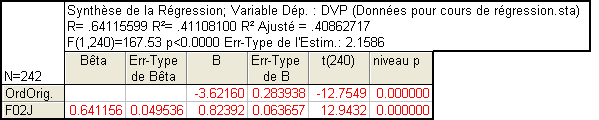
Si nous calculons la régression simple de DVP par F11VN, nous trouvons que F11VN explique environ 13% de la variance :
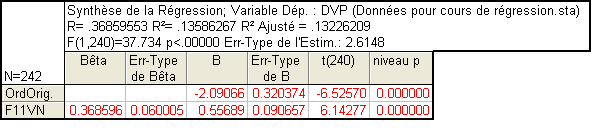
On pourrait donc s’attendre à ce qu’une régression prenant ces deux prédicteurs en compte explique 41+13=54% de la variance. Or, que trouvons-nous ?
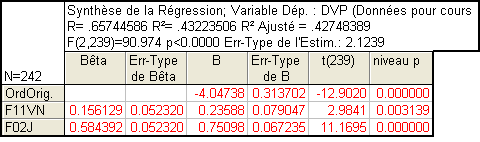
Le R² ajusté vaut .427 ce qui signifie que l’ajout de la variable F11VN explique en réalité moins de 2% de variance supplémentaire par rapport à ce qu'on avait avec F02J seule !
Un examen rapide de la corrélation entre les deux prédicteurs montre qu’en fait les deux VIs sont colinéaires :

En effet, les deux variables sont significativement corrélées et donc la variance expliquée par ces deux VIs sera donc généralement inférieure à la somme des variances expliquées par chacune d'elles prise séparément.
6.2. La multicolinéarité et son diagnostic
2.1. Définition de la multicolinéarité
La multicolinéarité est le fait qu’une VI est prédictible par (ou partage sa variance avec) une combinaison linéaire des autres VI. Pour faire simple, disons qu'une combinaison linéaire est une variable que l'on obtient en faisant la somme pondérée de plusieurs autres variables. Ainsi, si l'on crée une variable X3 en faisant la somme pondérée de deux autres variables X1 et X2, par exemple X3 = 2 X1 + 3 X2 , alors X1 , X2 et X3 seront multicolinéaires .
Du point de vue du diagnostic, la multicolinéarité se détecte en faisant la régression de l'une VI envisagée par les autres (on laisse provisoirement de côté la question de la VD). Le carré du R multiple obtenu dans cette régression représente la part de la variance de la VI expliquée par l'ensemble des autres VI. Cela représente donc en fait le degré auquel on peut dire qu'il existe une combinaison linéaire qui relie les VI. Idéalement, ce R² doit donc être minimal.
2.2. Définition de la tolérance
La tolérance est la part de la variance d'une VI qui n’est PAS expliquée par les autres VI. C'est donc le complémentaire à 1 du R² de la régression d'une VI par les autres VI (et qu’il ne faut surtout pas confondre avec le R² de la régression de la VD par les VI !!) :
Tolérance= 1- R².
Idéalement, elle doit être le plus élevé possible. Si la tolérance est plus petite que .10, cela mérite investigation. Si la tolérance est plus petite que .01, il n’est pas prudent (et en tout cas probablement peu intéressant) d’inclure la VI dans les analyses en plus des VI qui la prédisent.
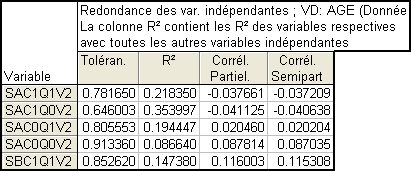
Voici un exemple issu des diagnostics de redondance de Statistica :
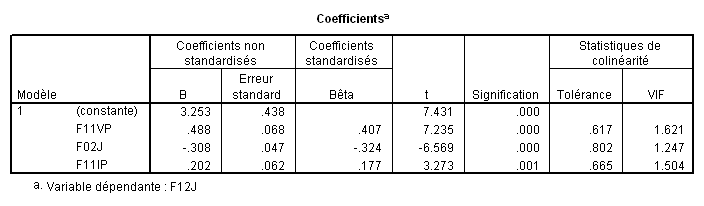
Voici un autre exemple issu de SPSS (avec l’option« tests de colinéarité » cochée) :
2.3. Facteur d'inflation de la variance
On remarque que SPSS donne aussi le « Facteur d'inflation de la variance » ou VIF (pour Variance Inflation Factor), qui est la valeur réciproque de la tolérance.
VIF= 1 / Tolérance
Des valeurs élevées de VIF indiquent donc la présence de multicolinéarité.
L’utilité diagnostique de cet indice résulte du fait que la variance du coefficient de régression augmente de la même façon que le facteur d'inflation de la variance. C’est pourquoi les tests de significativité des différents prédicteurs se trouvent améliorés par la suppression d’une VI qui induit de la multicolinéarité.
7. Régression linéaire multiple : Ordre d'introduction des variables
Objectifs. Sensibiliser à la problématique de l'ordre d'introduction des variables, les réponses possibles, et les analyses que permet chaque méthode.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur l'Approche intuitive
- Cours de L1 sur la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables : descriptive L1 / Inférentielle L2
- Régression simple approche descriptive (L1)
- Régression simple : approche inférentielle (L2) et notamment l'article précédent sur la redondance des VI
Résumé. L'article part du principe que l'étudiant dispose d'un logiciel de statistique pour réaliser les calculs. On présente les traitements à réaliser et comment interpréter les principales données produites par les logiciels.
7.1. Régression linéaire multiple : Ordre d'introduction des variables
1. Problématique de l'ordre d'introduction des variables
1.1. Retour sur la notion de multicolinéarité
L’existence d’un certain niveau de redondance entre les VIs pose la question de l’ordre dans lequel la contribution des différentes VIs sera analysée. Par exemple, soient 3 VIs, VI1, VI2 et VI3, ici en bleu, en jaune et en rouge respectivement. Le diagramme de Venn suivant montre la structure de la variance totale, avec des éléments de variance propre à chaque VI (zones en rouge, bleu et jaune) et des éléments de variance partagée (intersections, de couleurs mixées).
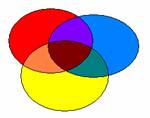
Toutes les méthodes de régression linéaire savent attribuer à chaque VI la variance qui lui est propre. Elles diffèrent sur la façon de répartir la variance partagée.
Le choix de la méthode d’introduction est d’importance majeure s’il s’agit d’évaluer la contribution relative des différentes Vis ou si l’on est en présence d’une forte colinéarité des VIs.
1.2. La Méthode Standard : Introduction Simultanée
Elle consiste à introduire toutes les variables en même temps dans l’analyse, mais à n’imputer à aucune variable en particulier la part de variance partagée. On n’impute à une variable que la part de variance qui lui est propre (les zones colorées dans le diagramme suivant).
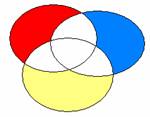
La part de variance partagée (régions en blanc) n’est pas totalement perdue : on la retrouve dans le calcul global de la variance expliquée par le modèle (le R² global).
1.3. Principe des Méthodes Hiérarchiques
Elles consistent pour le chercheur à déterminer un classement de priorité parmi les prédicteurs qu’il est potentiellement possible d’entrer dans l’analyse. Idéalement, ce classement sera fondé sur des bases théoriques.
On peut avoir plusieurs niveaux hiérarchiques, avec un bloc de variables à chaque niveau.
Admettons pour simplifier qu’il n’y ait qu’une VI par bloc. La variable prioritaire se taille la part du lion : elle se voit attribuer toute la variance partagée avec les variables de rang inférieur, lesquelles ne gardent que la part de variance qui leur est propre. Admettons, par exemple, que le chercheur ait des raisons théoriques de penser que la VI bleue soit plus importante que les autres, puis que la rouge soit plus importante que la jaune. Il va donc entrer d’abord la bleue dans le premier bloc. Elle recevra toute la variance qui la concerne, y compris ce qu’elle partage avec la rouge et la jaune. Puis la rouge, dans le deuxième bloc, recevra ce qui la concerne, y compris ce qu’elle partage avec la jaune, mais moins ce qui a déjà été attribué à la bleue. Enfin la jaune, dans le troisième bloc, ne recevra que ce qui la concerne en propre
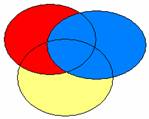
L'intérêt de cette approche est que la somme des variances expliquées par chaque VI est égale à la variance expliquée totale. Toutefois, l'attribution de la variable partagée à l'une des variables plutôt qu'aux autres est fondamentalement arbitraire (le choix d'attribuer en priorité la variance partagée à la variable qui explique le plus de variance propre est un choix tout aussi arbitraire qu'un autre)... De ce point de vue, les autres méthodes produisent une attribution différente, mais pas mieux fondée.
1.4. Principe des Méthodes Statistiques (ou « séquentielles »)
Elles consistent à introduire ou à retirer les variables une par une, comme dans le cas des variables hiérarchiques. Ce qui caractérise les méthodes statistiques, c’est que la hiérarchie est déterminée par le logiciel, sur des bases statistiques uniquement.
Ces méthodes sont très discutées car, lorsque plusieurs VI partagent une part substantielle de variance, elles conduisent à des résultats instables. En outre, leur sensibilité à des aspects mathématiques ne reposant sur aucune justification théorique propre au domaine étudié est aussi discutable.
Il existe plusieurs méthodes d’introduction séquentielle que nous allons détailler dans les sections suivantes de ce chapitre. Il existe aussi d’autres méthodes que nous laisserons de côté ici(e.g., la régression dite « ridge »).
1.5. Combinaison des types de Méthodes
Des logiciels comme SPSS permettent de combiner les différentes méthodes.
Par exemple, si le chercheur répartir 12 VIs entre 3 blocs hiérarchiques de 4 VIs chacun, il peut déterminer la méthode d’introduction qui sera utilisée à l’intérieur de chaque bloc.
Par exemple,l’introduction traitement des VI du bloc 1 peut être réalisée la méthode standard tandis qu’ensuite le traitement du bloc 2 sera réalisé par une méthode statistique.
Pour une comparaison des avantages et inconvénients de chaque méthode, voir par exemple Tabachnick et Fidell (1996).
7.2. Exemple d’Analyse par la méthode standard
Reprenons l’exemple précédent, où l’on veut prédire la VD « DVP » à partir des VIs« F02J » et « F11VN ». Ajoutons en outre trois nouvelles VIs « F11VP » « F11EN » et « F11EP ».
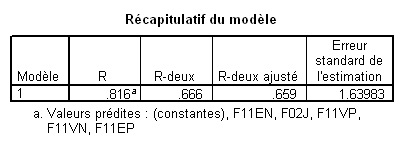
Voici ce que donne la méthode standard sous SPSS


Examinons ces résultats de plus près, en nous limitant à ce que nous n’avons pas déjà vu jusqu’ici.

Ce tableau des sorties de SPSS semble nouveau car, jusqu’à présent, nous ne l’avions pas présenté. Il rend compte de la méthode d'introduction des variables.
Colonne Modèle : donne le numéro du modèle testé. Avec la méthode standard, il n’y en a qu’un puisque tout est entré d’un seul coup.
Colonne Méthode : comme son nom l’indique, c’est la méthode de régression utilisée. Pour les régressions pas à pas, à chaque étape de la procédure, un nouveau modèle est calculé. Une nouvelle ligne sera donc créée pour chaque modèle, qui indiquera les variables introduites et exclues de ce modèle.
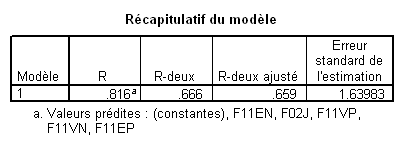
Notez simplement dans ce tableau d’ajustement que R ² ajusté signale que le modèle avec les cinq VI explique 65.9% de la variance totale.
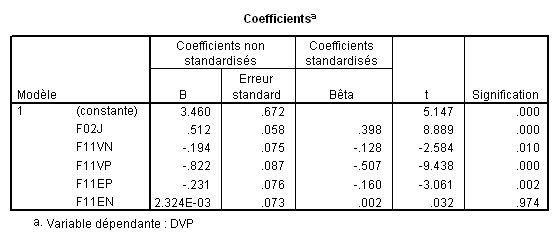
Ici, nous voyons que 4 VI contribuent significativement et la 5e pas du tout.
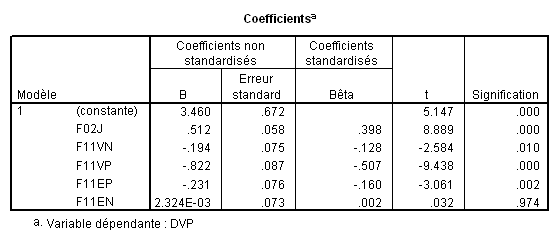
Observez les valeurs des bêtas, dont la valeur absolue traduit l’importance relative des variables dans la régression : On voit que F11VP contribue fortement aux variations de la VI, puis F02J, F11EP, F11VN et finalement F11EN qui contribue tellement peu que cette contribution n’est pas significative.
7.3. La Méthode Statistique Ascendante
Elle consiste à introduire les variables une par une. À chaque étape, le modèle comprenant l’ensemble des VI sélectionnées est alors recalculé avec la méthode standard.
Analysons la sortie de SPSS obtenue avec les données de l’exemple précédent, mais en adoptant la méthode pas à pas.

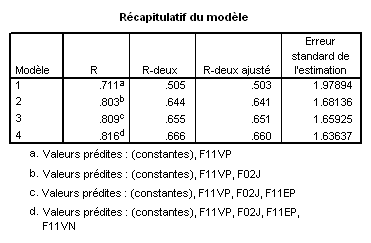
On voit ici que 4 modèles ont été construits successivement.
On peut remarquer que l’ordre d’introduction des variables correspond à l’ordre d’importance des contributions relatives tel qu’il apparaissait dans la méthode standard.
On peut aussi remarquer que le processus s’arrête avant l’introduction de la variable F11EN : celle-ci contribue tellement peu qu’elle n’atteint pas le critère d’introduction dans un nouveau modèle. Ce critère est un paramètre que le chercheur peut fixer. Généralement, on utilise le seuil classique de p = .05. Il faut noter ici que, comme pour toutes les méthodes d’analyses statistiques, une contribution non significative ne signifie pas forcément absence de contribution. Il se peut que la variabilité des données soit simplement trop grande devant la taille de l’effet de la variable pour que le test de signification puisse détecter cet effet. La même analyse conduite avec un nombre beaucoup plus élevé de sujets conserverait peut-être cette variable.
Fort logiquement, le R ² ajusté des modèles augmente avec chaque variable introduite, et tout aussi logiquement, cette augmentation est de plus en plus faible avec l’introduction de variables de moins en moins contributives.
Il est crucial de remarquer ici la différence d’évolution des valeurs de R² et de R² ajusté. Le R² ne diminue jamais avec l’augmentation du nombre de VI. Il n'en va pas de même pour le R² ajusté. Au contraire, si l’on compare le modèle 4 de ce tableau avec le modèle donné dans l’exemple de la méthode standard, nous voyons que la prise en compte de la variable F11VN dans la méthode standard n’a strictement rien ajouté à la capacité prédictive brute du modèle : le R² est le même (.666) dans les deux cas. Toutefois, le R² ajusté est meilleur dans le modèle obtenu dans ce cas par la méthode pas à pas. Ceci traduit tout simplement le principe de parcimonie (le fameux « rasoir d’Occam ») : le modèle avec moins de VIs est plus parcimonieux, et puisqu’il a le même pouvoir de prédiction, il est donc meilleur.
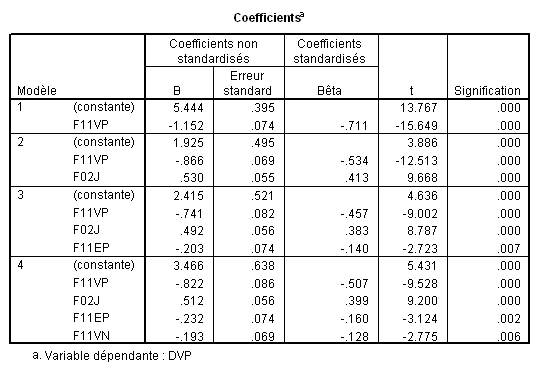
L’analyse du tableau des coefficients montre bien que les coefficients d’une même variable changent selon le modèle considéré. Par exemple, la variable F11VP a un bêta de -.711 lorsqu’elle est seule, mais il tombe à -.534 lorsqu’il est calculé en même temps que la variableF02J.
7.4. La Méthode Statistique Descendante
Le principe est exactement le contraire de celui de la méthode ascendante. On introduit d'abord toutes les VI possibles et on applique la méthode standard. Ensuite, les variables dont la probabilité de contribution n’atteint pas un certain seuil sont progressivement éliminées, une par une. Ce critère d’élimination est un paramètre que le chercheur peut fixer. Généralement, on utilise le seuil de p =.10. On remarquera que cette valeur est plus prudente que celle du critère d’introduction.
En reprenant les données précédentes, cela donne ceci :


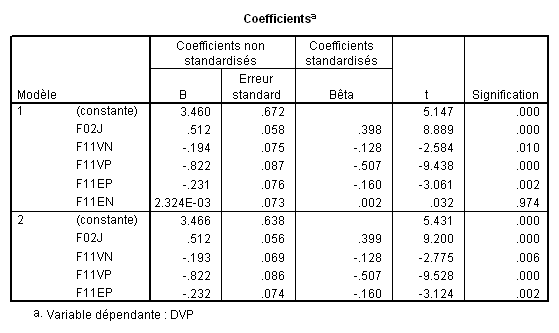
On voit ici que la méthode descendante permet de savoir ce qu’on perd en éliminant une variable donnée, mais ensuite la distribution des contributions est la même qu’avec la méthode standard. Bien entendu, la variance totale expliquée reste identique à celle obtenue dans les autres méthodes.
7.5. La Méthode Pas à Pas
Elle combine les deux méthodes précédentes, introduction et élimination, au sens où le processus commence par une démarche ascendante (introduction progressive), mais si la contribution d’une variable déjà introduite tombe en dessous du critère d’élimination, elle est retirée du modèle.
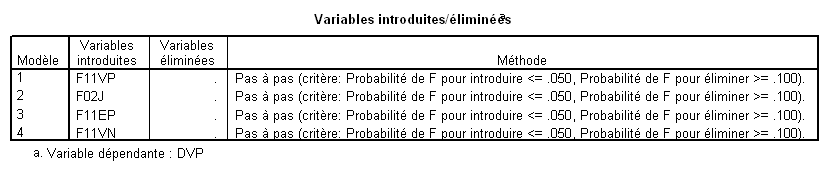
7.6. Répartition entre VIs des parts de variance expliquée
6.1. Principe général
Si l’on veut maintenant évaluer la contribution respective des différentes VI, laquelle prendre ?
Il n’y a pas une réponse unique à cette question mais eu égard aux schémas que nous avons présentés plus haut, voici ce que cela donne (il faut juste transposer le principe de ces schémas à 3VIs au cas à 4 Vis):
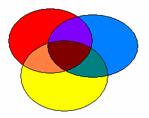
Ce schéma représente la répartition totale de la variance, que l’on cherche à connaître.
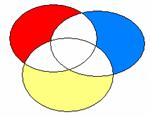
Ce schéma correspond à la méthode standard appliquée au modèle à 4 VIs. Les bêtas sont ceux du modèle 4. Si la zone bleue correspond à la part de variance attribuée à F11VP, le bêta correspondant est donc -.507. Etsi la zone rouge correspond à F02J, son bêta est .399.
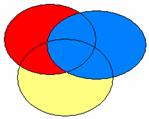
Ce schéma correspond à la méthode hiérarchique si le chercheur a mis la zone bleue dans le premier bloc, le rouge dans le second, et le jaune dans le troisième. Il correspond aussi à une méthode statistique lorsque celle-ci a conduit à la même hiérarchie des VIs.
Si la zone bleue correspond à la part de variance attribuée à F11VP, le bêta correspondant est celui qu’il possède dans le modèle 1 (-.711). Si la zone rouge correspond à la part de variance attribuée àF02J correspond à la zone rouge, son bêta est celui du modèle 2, soit .413. De façon générale, le bêta correspondant à la part de variance attribuable à une VI donnée est celui donné par le premier modèle où cette variable à été introduite (on prendra donc -.16 pour F11EP et -.128 pour F11VN).
Évidemment, toutes ces différences ne sont sensibles que si les zones d’intersection sont non vides. Autrement dit, s’il existe de la colinéarité entre les VI.
C’est pourquoi, préalablement à tout questionnement sur l’importance relative des VIs, il convient d’examiner la matrice de corrélation des VIs entre elles.
6.3. Corrélations semi-partielles
On appelle « carré de la corrélation semi-partielle d’une VI i », la réduction de R² induite par la suppression de cette VI de l’analyse. C’est donc la contribution propre de la VI au R² dans cet ensemble de VIs. On note sr i ² le carré de la corrélation semi-partielle et
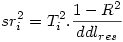
où Ti est le t de student de la i ème VI, et ddlres le nombre de degrés de liberté résiduels.
Pour illustrer cela, examinons une sortie de SPSS.
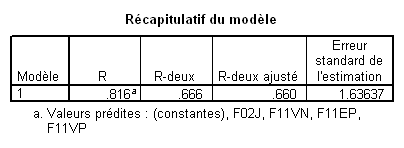
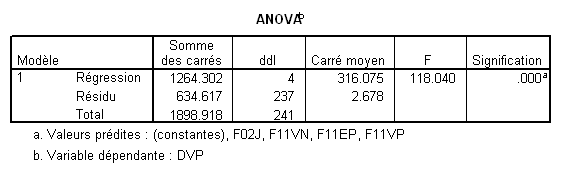
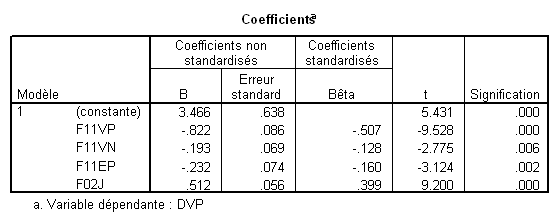
Prenons la variable F02J par exemple. Son t est 9.2, le ddl des résidus dans l’ANOVA est 237, et le R² est .666. Cela donne donc
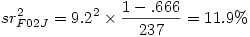
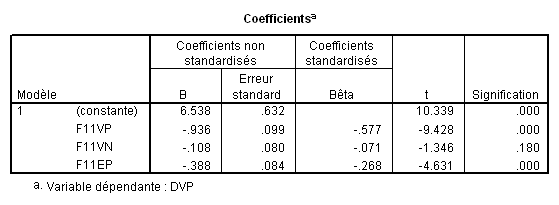
On s’attend donc à ce qu’une nouvelle analyse sans F02J donne un R² de .666 - .119= .547
Ce que nous vérifions immédiatement (aux erreurs d’arrondi près) :

Dans les méthodes hiérarchique et statistique, où toute la variance est attribuée aux prédicteurs, la somme des carrés des corrélations semi-partielles est R² .Dans la méthode standard, où la variance partagée n’est attribuée à aucune VI en propre, cette somme est inférieure à R² .
Pour terminer, signalons qu’il est possible d’obtenir directement les corrélations semi-partielles. Par exemple dans SPSS une option permet d’obtenir :
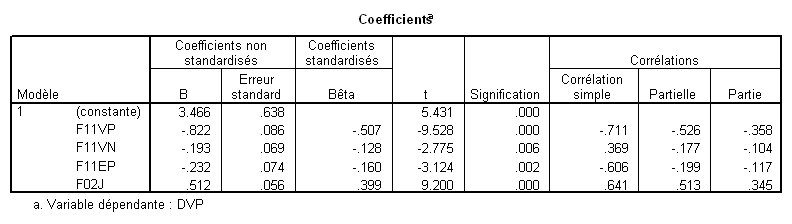
On voit apparaître la corrélation semi-partielle dans la colonne la plus à droite. Mais attention : il faut encore l’élever au carré pour pouvoir l’interpréter en termes de part de variance expliquée par le prédicteur.
7.7. Méthode d'introduction et Inférence statistique
7.1 Test des composants de la régression (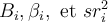 )
)
Dans la méthode standard, le test de signification est le même pour 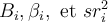 .
.
B / Erreur standard de B
Il teste si la VI considérée explique une part significativement plus élevée de la variance de la VD, indépendamment de la variance partagée avec les autres VI. Ce qui signifie que si deux VIs sont très corrélées, l’une des deux peut se retrouver non significative. D’où l’importance pour l’évaluation globale des résultats de rapporter la matrice de corrélations complète.
Dans les méthodes hiérarchique et statistique, les tests de
Bi
et 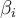 restent les mêmes que ceux de la méthode standard, mais les tests de
restent les mêmes que ceux de la méthode standard, mais les tests de 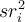 changent.
changent.
Par elle-même, la valeur de 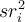 peut se calculer sur la base du fait que dans ces méthodes, la somme des
peut se calculer sur la base du fait que dans ces méthodes, la somme des 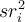 est précisément le R². Par conséquent, la différence des R² avant et après l’introduction de la ième VI donne directement le
est précisément le R². Par conséquent, la différence des R² avant et après l’introduction de la ième VI donne directement le 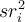 .
.
Prenons comme exemple le modèle hiérarchique suivant :

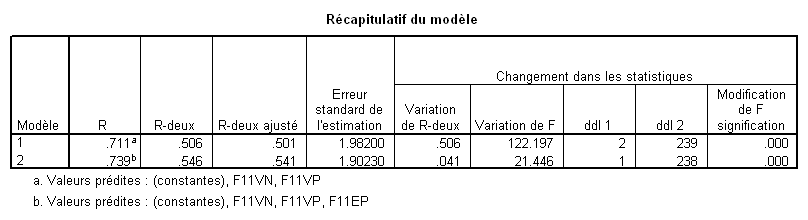
On se demande quelle part de variance ajoute F11EP dans un contexte où F11VN et F11VP ont été introduites à un niveau hiérarchique supérieur. Pour le savoir, il suffit de faire la différence des R² avant et après introduction : .546 - .506 = .04 soit 4% de variance expliquée. Cela apparaît dans la colonne « variation de R-deux ». Cette différence est-elle significative ? Oui, comme l’indique la colonne « Modification de F, signification. ».
Autrement dit, ajoute la variable F11EP dans le contexte du bloc hiérarchiquement supérieur composé par F11VN et F11VP accroît significativement le pouvoir explicatif du modèle.
7.2 Intervalles de confiance autour de B
On calcule l’intervalle de confiance d’un paramètre pour estimer sa valeur dans la population parente à partir de sa valeur observée dans l’échantillon et d’un risque que l’on accepte de prendre. Si l’intervalle de confiance contient la valeur 0, on accepte alors l’hypothèse nulle (absence de liaison dans la population parente).
Les bornes de l’intervalle de confiance sont données par l’équation :
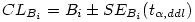
La valeur de t à utiliser est donnée par la loi de Student inverse qui prend deux paramètres, le risque α et le nombre de degrés de libertés, soit n -2.
Reprenons l’exemple où F11VN et F02J sont pris comme prédicteurs de DVP par la méthode standard. Sous SPSS, en demandant les intervalles de confiance on obtient directement :
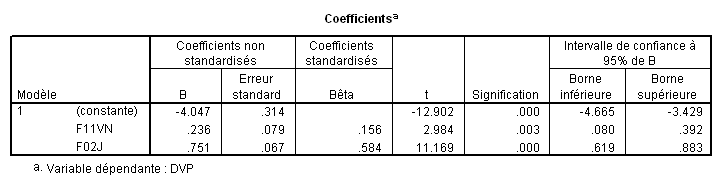
Dans notre exemple, n = 242, soit 240 ddl. Si l’on choisit comme risque α = 5%, c’est-à-dire qu’on veut que 95% des mesures tombent dans l’intervalle de confiance, la loi de student inverse pour 240 degrés de libertés et un risque de 5% donne t = 1.97.
L’intervalle de confiance de F02J est donc [.751-1.97*.067 ;.751+1.97*.067],
soit [.619 ;.883]
Ce qui signifie que dans 95% des cas, si l’on mesure la valeur de B, on trouvera une valeur comprise entre .080 et .392 pour F11VN, et entre .619 et .883 pour F02J.
Attention : ces valeurs ne sont pas comparables d’une VI à l’autre, puisque ce sont des intervalles de confiance d’un paramètre non standardisé.
Si l’on souhaite utiliser un risque α = 5%, il suffit donc de prendre les valeurs données par SPSS, et si l’on veut un autre risque, la formule est très simple à adapter. La valeur souhaitée de t s’obtient facilement sous un tableur (ici la formule était « =LOI.STUDENT.INVERSE(.05;240) »).
7.8. Comparaison de deux ensembles de prédicteurs
Il s’agit de déterminer si un ensemble de VIsE1 prédit la VD mieux qu’un autre ensemble de VIs, E2.
Fondamentalement, il s’agit donc de comparer la corrélation multiple entre E 1 et la VD avec la corrélation multiple entre E 1 et la VD. On pourrait penser qu’il suffit de prendre les deux R multiples, et les introduire dans une banale comparaison de corrélations, comme nous appris à les faire ici). Le problème est que les corrélations à comparer ne sont pas indépendantes, comme l’assume le test que nous avons vu, mais partagent une variable commune, à savoir la VD.
Une solution est possible d’après Steiger(1980). La méthode est la suivante :
1°) On enregistre les scores prédits par chacune des deux modèles dans deux nouvelles variables.
2°) On calcule la corrélation entre ces deux variables.
À ce moment, on dispose de trois corrélations.
- Appelons ra la corrélation multiple entre la VD et l’ensemble de VIs E1 .
- Appelons rb la corrélation multiple entre la VD et l’ensemble de VIs E2 .
- Appelons rab la corrélation entre les prédictions des deux ensembles de VIs.
3°) on applique la transformation de Fisher à ces corrélations (rappelons que c’est la fonction arctangente hyperbolique, ce qui donne deux corrélations transformées ra' et rb' avec
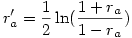
et
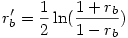
4°) On calcule ensuite
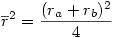
5°) puis
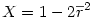
6°) On calcule alors
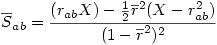
7°) Finalement la variable
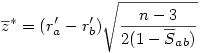
suit une loi normale classique.
7.9. Conclusion : Choix d’une méthode
La force de la méthode standard est que les contributions propres de chaque VI sont indiscutables et ses résultats sont stables. C’est pourquoi Tabachnick et Fidell la recommandent par défaut.L’inconvénient de cette méthode est les contributions des VIs sont souvent sous-estimées puisque seule la part de variance qu’elles sont seules à expliquer dans l’ensemble des VIs de référence leur est imputée. Cela a pour conséquence de réduire la valeur des bêtas, ce qui ensuite peut conduire à éliminer une variable comme non significativement contributive alors même que la corrélation de cette variable avec la VD peut être très forte.
L’intérêt de la méthode hiérarchique est le contrôle que le chercheur exerce sur l’introduction des variables, ce qui lui permet de tester des hypothèses théoriques ou de donner priorité à des variables dont on sait d’après la littérature qu’elles sont contributives.
Parmi les méthodes statistiques, la méthode pas à pas est généralement considérée comme celle conduisant aux résultats les plus fiables. Le reproche que l’on fait à cette procédure est qu’elle « capitalise sur la chance ». Le résultat est que l’équation de régression tend à modéliser l’échantillon plutôt que la population dont il est tiré (on décrit du bruit au lieu de modéliser le signal caché derrière le bruit). Pour cette raison, une validation croisée est recommandée : l’ensemble des données est partitionné en deux sous-fichiers par tirage aléatoire. Le premier sous-fichier sert à construire le modèle, le second fichier sert à tester si le modèle se généralise bien à des données externes à celles de l’échantillon qui ont servi à la construire.
Selon Tabachnick et Fidell (1996) :
_ La méthode standard répond à 2 questions :
(1) quelle est l’importance globale de la relation entre la VD et l’ensemble des VIs
(2) À quel degré chaque VI contribue-t-elle de façon unique à la VD ?
_ La méthode hiérarchique répond à la question :
(1) Est-ce que l’ajout d’une k ième VI dans le modèle augmente significativement la prédiction de la VD par rapport au modèle composé des k-1 VIs précédentes ?
_ La méthode statistique répond aux questions :
(1) Quelle est la combinaison linéaire de VIs qui prédit le mieux la VD dans l’échantillon testé ?
8. Régression linéaire : Évaluer la qualité de la relation
Objectifs. Apprendre à évaluer la qualité d'une régression simple.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur l'Approche intuitive
- Cours de L1 sur la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables : descriptive L1 / Inférentielle L2
- Régression simple approche descriptive (L1)
- Régression simple : approche inférentielle (L2)
Résumé. Trois types de critères d'évaluation sont examinés : la normalité des résidus, l'homoscédasticité ou l'hétéroscédasticité, et le fait que les résidus ne devraient pas pouvoir être prédits.
8.1. Introduction
Lorsque l’on fait de la modélisation (linéaire ou non), il est bien sûr intéressant d’examiner la qualité de la relation entre les données et les valeurs prédites. Une approche positive consiste à examiner la corrélation entre valeurs observées de la VD et valeurs prédites. Une approche complémentaire consiste à examiner ce qui se passe quand le modèle ne donne pas des valeurs identiques aux valeurs prédites, c’est-à-dire à analyser les écarts entre valeurs prédites et valeurs observées, ce qu'on appelle les résidus.
Fondamentalement, l’analyse des résidus en modélisation linéaire consiste à évaluer comment les résidus sont distribués en fonction des valeurs prédites de la variable dépendante. Les résidus d’un bon modèle présentent diverses propriétés : normalité, linéarité, homoscédasticité, et indépendance. Nous allons maintenant les définir d’un point de vue théorique.
Pour diagnostiquer les diverses anomalies des résidus, les logiciels de statistiques proposent divers outils que nous allons examiner dans les pages suivantes.
8.2. Normalité globale des résidus
Normalité : Si le modèle est idéalement bon, alors les écarts que l’on constate entre les valeurs prédites et les valeurs observées (les résidus donc) sont entièrement imputables à des erreurs de mesure. De ce fait, les résidus doivent posséder les propriétés classiques d’une distribution normale : courbe « en cloche », symétrique autour de la valeur prédite, avec un aplatissement régulier des extrémités. En cas de violation de cette assomption, les tests de signification risquent d’être biaisés.
La première chose est de vérifier si, globalement, les résidus sont bien normalement distribués.
Sous Statistica, on peut par exemple obtenir la « droite de Henry » qui met en relation les valeurs observées des résidus (abscisses) avec des valeurs z construites sous l’hypothèse que la distribution des résidus est normale. Idéalement, on doit avoir l’identité, c'est-à-dire que tous les points du graphe doivent être situés sur la droite en rouge. Ici, le résultat est assez satisfaisant, encore qu’un très léger biais apparaît aux valeurs extrêmes.
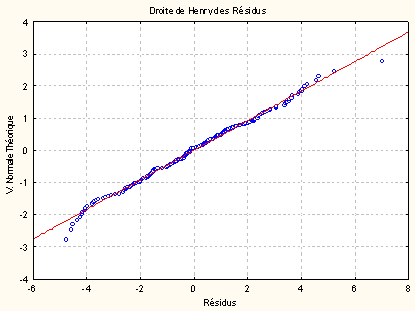
Sous SPSS, on peut demander un « diagramme P-P ». Le principe, assez similaire à celui de la droite de Henry utilisée dans Statistica, est de construire un diagramme mettant en relation la probabilité cumulée d’apparition d’une valeur avec sa probabilité théorique.
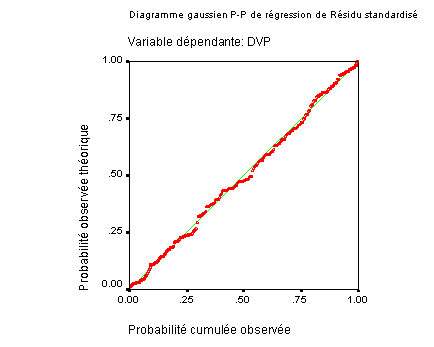
Si vous avez des doutes sur la normalité de la distribution des résidus, une stratégie qui permet d’obtenir des informations plus détaillées sur la normalité des résidus consiste à commencer par enregistrer ceux-ci comme de nouvelles variables (option disponible sous SPSS comme sous Statistica), puis à appliquer les procédures générales de test de la normalité d’une variable.
8.3. Normalité des résidus en fonction des valeurs prédites
3.1. Présentation du problème
Une première approche consiste à produire le nuage de points que l’on obtient en prenant les valeurs prédites comme abscisses et les résidus comme ordonnées.
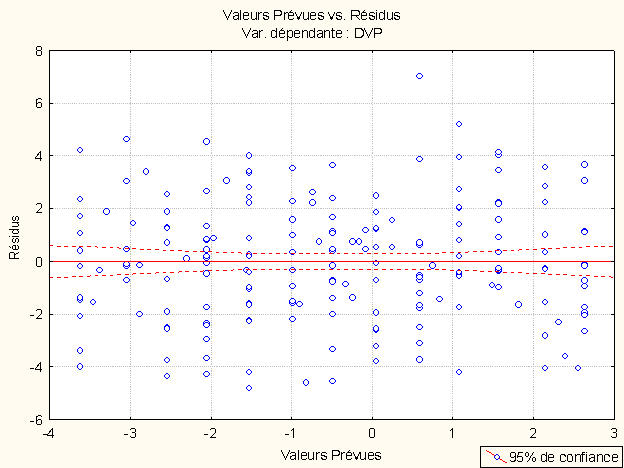
Selon Tabachnick et Fidell (1996), « si toutes les assomptions sont remplies, les résidus seront distribués presque rectangulairement avec une concentration de scores le long du centre » (p. 137). On peut bien sûr dessiner des cas d’école mais, sur de vraies données, comme on le voit sur notre nuage de points, tout le problème est de savoir ce que l’on entend par « presque » !!
3.2. Définitions
L'homoscédasticité s'observe lorsque la dispersion des résidus est homogène sur tout le spectre des valeurs de la VI. C'est une propriété souhaitable puisque si les résidus correspondent bien à des aléas de mesure, il n’y a pas de raison que la dispersion de ces résidus change en fonction des valeurs du prédicteur.
Si la dispersion des résidus n’est pas homogène, on parle d’hétéroscédasticité. Sur le schéma précédent, la dispersion des résidus autour des valeurs prédites est symbolisée par les deux courbes pointillées autour de la droite. Idéalement, ces courbes devraient être parallèles à la droite.
L’analyse de l’homoscédasticité est l'équivalent, pour les prédicteurs continus d'une régression, de l’analyse de l’homogénéité des variances entre les groupes dans une ANOVA ou un test de student (par exemple au moyen d'un test de Levene).
3.3. Origines de l'hétéroscédaticité
L’hétéroscédasticité apparaît
- si l’une des deux variables n’est pas normale.
- s’il existe une relation particulière entre les deux variables. Par exemple, une relation entre l’âge et le salaire : plus les gens avancent en âge et plus il y a de variations dans les salaires.
- si l’erreur de mesure change selon les niveaux des variables
Par exemple, si à un certain âge les gens sont plus concernés par leur poids, ils en donneront des estimations plus fiables que celles des gens moins ou plus âgés. La variance des estimations données par les individus sera donc plus faible aux valeurs moyennes de la pyramide des âges qu’aux extrêmes.
Pour la régression linéaire, il me semble que le test de l’homoscédasticité est essentiellement utile à la compréhension de la structure des données (nécessité de transformation, etc.)
8.4. Non-prédictibilité des résidus
La non-prédictibilité des résidus est l'idée qu’il ne doit pas exister de relation visible entre les résidus et les valeurs prédites de la variable dépendante.
Deux points sont à noter à ce sujet : le problème de la linéarité et celui de l'indépendance.
4.1. Linéarité et non-prédictibilité des résidus
Si on trouve une relation curvilinéaire entre les résidus et les valeurs prédites, c’est qu’il manque un prédicteur non linéaire dans le modèle. Autrement dit, d'une part le modèle manque de validité puisqu'il lui manque un prédicteur, et d'autre part l’assomption de linéarité de la relation entre VI et VD est violée. Ce constat ne remet pas en cause la capacité prédictive du modèle lui-même, telle qu'on l'a constatée, mais indique qu’il serait possible de construire un meilleur modèle en ajoutant un autre prédicteur, linéaire ou non et/ou en appliquant une transformation non linéaire à l’une des variables en jeu dans la relation.
Techniquement, on peut détecter une non-linéarité dans les résidus en sortant le diagramme de dispersion prenant comme abscisses les valeurs standardisées de la VI, et comme ordonnées les valeurs standardisées des résidus (cf. Point précédent).
Un point qu’il faut toujours avoir à l'esprit est qu’une relation non linéaire en soi, peut parfois se laisser capturer assez bien par une relation linéaire. Prenons l’exemple de la fonction Y = X ², si on se cantonne au domaine des valeurs de X prises entre 0 et 10 :
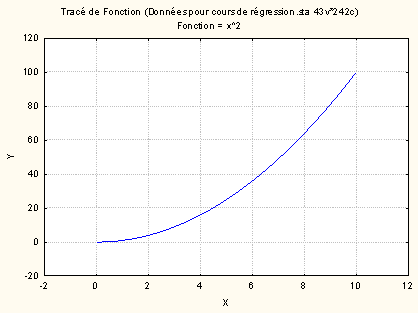
On devine sans difficulté que le nuage de points dérivé de cette fonction serait expliqué très largement par une fonction linéaire. Mais la même fonction prise entre -10 et 10 ne se laisse plus du tout ramener à une droite :
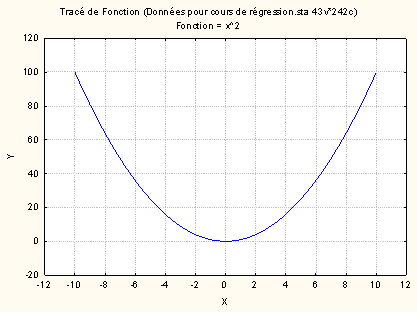
Conclusion : il faut être prudent dans l’interprétation des courbes de régression. Observer une relation d’apparence linéaire ne signifie pas nécessairement que la relation sous-jacente est véritablement linéaire. En outre, on comprend pourquoi le modèle linéaire connaît un tel succès : il peut souvent rendre compte de données qui en fait ne le concernent pas. De ce fait, si la régression linéaire est un bon outil pour mettre en évidence l’existence d’une relation, et bien qu’il puisse constituer un bon outil de prédiction, du point de vue de la production de connaissances théoriques, il vaut mieux disposer d’une approche expérimentale si l’on veut prouver quelque chose !
4.2.Indépendance
Les erreurs de prédiction doivent aussi être indépendantes les unes des autres.
9. Questionnaire d'auto-évaluation
Ce QCM comprend 10 questions. Répondez à chaque question puis, à la fin, lorsque vous aurez répondu à toutes les questions, un bouton "terminer" apparaîtra sur la dernière question. En cliquant sur ce bouton, vous pourrez voir votre score et accéder à un corrigé.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte