Rappels de maths pour le cours de L2
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L2 |
| Livre: | Rappels de maths pour le cours de L2 |
| Imprimé par: | Visiteur anonyme |
| Date: | vendredi 13 février 2026, 08:03 |
Description
1. Application
Objectifs . Définir une application.
Prérequis. Aucun.
Résumé. Une relation R reliant les éléments d'un ensemble E aux éléments d'un ensemble F est une application si tout élément de E a exactement une image dans F.
A. Préalable
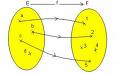
Considérons deux ensembles non vides E et F, et la relation notée R qui relie les éléments de E aux éléments de F. La figure ci-dessus est une relation de ce type.
Remarques
- On appelle une telle relation une relation binaire parce que les éléments reliés forment des couples, comme par exemple le couple (a, 1).
- L'ensemble E s'appelle l'ensemble de départ de la relation.
- L'ensemble F s'appelle l'ensemble d'arrivée de la relation.
- Rien n'empêche de définir une relation d'un ensemble dans lui-même, auquel cas cet ensemble sert d'ensemble de départ et d'ensemble d'arrivée.
B. Définition
On appelle application une relation binaire qui, à tout élément de l'ensemble de départ, associe exactement un élément de l'ensemble d'arrivée.
Soit R une application de E dans F, et soit a R 1. On dit que 1 est l'image de a par R, et que a est l'antécédent de 1 par R.
C. Exemple et contre-exemples
Exemple : considérons l'ensemble des êtres humains amoureux et imaginons que les humains amoureux n'aient qu'une relation amoureuse à la fois. La relation "est amoureux de" est une application.
Contre-exemple 1 : si on considère qu'un être humain peut être amoureux de plusieurs personnes à la fois, alors la relation "est amoureux de" n'est pas une application puisqu'il existe au moins un être humain qui est amoureux d'au moins deux personnes.
Contre-exemple 2 : considérons maintenant l'ensemble des êtres humains tout court. La relation "est amoureux de" n'est pas une application puisqu'il existe au moins un être humain qui n'est amoureux de personne.
2. Injection, surjection, bijection
Objectifs . Définir une injection, une surjection et une bijection.
Prérequis.
Résumé. Une relation R reliant les éléments d'un ensemble A aux éléments d'un ensemble B est une bijection si elle est injective et surjective.
1. Injection
Une application de A dans B est injective si deux éléments distincts de A ont des images distinctes.
Remarque. Une description psychologique est une application d'un ensemble de couples (personne, date) dans un ensemble de modalités descriptives. Une description injective signifie que deux couples différents n'ont pas la même description. Connaissant la description, on peut identifier le couple décrit.
2. Surjection
Une application de A dans B est surjective si tout élément de B a au moins un antécédent.
Remarque. Une description psychologique est surjective si toutes les descriptions possibles ont au moins un antécédent. Lorsque le référentiel de description a une taille plus grande que la taille de l'échantillon des personnes décrites (en fait, des couples (personne, date) décrits), la description n'est pas surjective.
3. Bijection
Une application de A dans B est bijective si c'est une correspondance terme à terme. Si c'est une injection et une surjection, c'est une bijection.
Démonstration. Si c'est une surjection, alors tout élément de B a au moins un antécédent. Si c'est une injection, chaque élément de A a une image spécifique. Donc toute image a un seul antécédent et c'est une correspondance terme à terme.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte