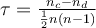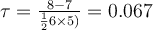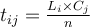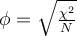Liaisons entre variables non numériques
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L1 |
| Livre: | Liaisons entre variables non numériques |
| Imprimé par: | Visiteur anonyme |
| Date: | dimanche 22 février 2026, 00:25 |
Description
Objectifs.
Étendre le concept de liaison entre variables, de corrélation, aux cas où les variables considérées ne sont pas toutes numériques.
Prérequis.
Résumé.
Le principe général de corrélation ayant été vu dans le cas numérique, le présent article présente des extensions à un petit nombre de cas particuliers importants : Deux variables ordinales ( rédaction : Éric Raufaste
 de Spearman et
de Spearman et  de Kendall); Deux variables nominales...
de Kendall); Deux variables nominales...
1. Liaison entre deux variables ordinales
A. Le  de corrélation des rangs de Spearman
de corrélation des rangs de Spearman
Le coefficient  (rho) de Spearman se calcule exactement comme le coefficient de corrélation linéaire à un point près : on commence par recoder les deux variables en termes de rangs avant de faire le calcul de la corrélation. Pour illustrer cela, imaginons les données suivantes, pour lesquels nous voulons calculer une corrélation de rangs entre les variables V1 et V2 :
(rho) de Spearman se calcule exactement comme le coefficient de corrélation linéaire à un point près : on commence par recoder les deux variables en termes de rangs avant de faire le calcul de la corrélation. Pour illustrer cela, imaginons les données suivantes, pour lesquels nous voulons calculer une corrélation de rangs entre les variables V1 et V2 :
Sujet V1 V2
1 1,1 3,4
2 5 6,5
3 2,4 2,8
4 3 1
5 3 2
6 2 1
Ce recodage en termes de rangs se fait selon la logique suivante : les observations sont ordonnées de la plus petites à la plus grande (ou l'inverse). La plus forte prend le rang 1, la deuxième le rang 2, etc... Pour ce qui concerne les ex-aequo, on remplace simplement leur valeur par la moyenne des rangs obtenus par cette valeur. Dans l'exemple précédent, la variable V1 donne le reclassement suivant (du plus grand au plus petit) :
Sujet V1 rang
1 1,1 6
2 5 1
3 2,4 4
4 3 2
5 3 3
6 2 5
La valeur 3 prend les rang 2 et 3, ce qui fait un rang moyen de 2,5 pour chacune de ces deux valeurs et finalement nous avons le recodage suivant :
Sujet V1 V1R
1 1,1 6
2 5 1
3 2,4 4
4 3 2,5
5 3 2,5
6 2 5
On applique la même logique sur la variable V2 et on obtient une variable recodée V2R:
Sujet V2 V2R
1 3,4 2
2 6,5 1
3 2,8 3
4 1 5,5
5 2 4
6 1 5,5
Si nous calculons alors la corrélation linéaire classique entre les variables V1R et V2R, nous trouvons la valeur 0,161 qui est le rho de Spearman.
Le rho de spearman s'interprète exactement comme une corrélation classique, qui varie entre -1 et +1, avec 0 signifiant l'absence de corrélation.
Pour calculer le  de Kendall, il faut commencer par trier les observations par ordre croissant (ou décroissant de l'une des deux variables). Cela nous donne donc un ordre parfait (aux ex aequo près) sur la première variable, mais pas sur la deuxième variable. On va alors comparer toutes les paires possibles de valeurs à l'intérieur de la seconde variable. On appellera
paire concordante
une paire qui ira dans le même sens que la variable n°1 et
paire discordante
toute paire qui ne va pas dans le même sens que la variable n°1. Le
de Kendall, il faut commencer par trier les observations par ordre croissant (ou décroissant de l'une des deux variables). Cela nous donne donc un ordre parfait (aux ex aequo près) sur la première variable, mais pas sur la deuxième variable. On va alors comparer toutes les paires possibles de valeurs à l'intérieur de la seconde variable. On appellera
paire concordante
une paire qui ira dans le même sens que la variable n°1 et
paire discordante
toute paire qui ne va pas dans le même sens que la variable n°1. Le  de Kendall s'obtient alors par la formule suivante :
de Kendall s'obtient alors par la formule suivante :
où
nc
est le nombre de paires concordantes et
nd
le nombre de paires discordantes.
Voyons cela sur un exemple. Nous partons des données suivantes :
Sujet V1 V2
1 1,1 3,4
2 5 6,5
3 2,4 2,8
4 3 1
5 3.2 2
6 2 1,1
En triant ces données selon la variable V1, nous obtenons :
Sujet V1 V2
1 1,1 3,4
6 2 1,1
3 2,4 2,8
4 3 1
5 3.2 2
2 5 6,5
Nous nous intéressons maintenant aux paires de données de la variable V2. Nous allons compter comme discordantes toutes les paires d'observations où la seconde valeur sera plus petite que la première (elles vont dans le sens inverse de l'ordre défini pour la variable V1) et concordantes les paires telles que la deuxième valeur est plus grande que la première. Ainsi, si nous comparons les sujets 1 et 6, nous voyons que la première valeur (3,4) est plus grande que la seconde (1,1) et donc la paire est discordante puisqu'elle ne va pas dans le même sens que l'ordre de la variable V1 (du plus petit au plus grand). Nous comptons encore 1 discordance pour la comparaison des sujets 1 et 3, etc... la paire sujet 1 - sujet 2 par contre est concordante (puisque 3,4 est plus petit que 6,5). Nous continuons avec la paire sujet 6 - sujet 3 qui est concordante). Nous examinons ainsi toutes les paires possibles, ce qui nous donc nc = 8; nd = 7. Si nous appliquons la formule plus haut, nous trouvons donc
Notons que le dénominateur de la formule, 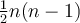 , représente le nombre total de paires possibles. Il y a en effet
, représente le nombre total de paires possibles. Il y a en effet 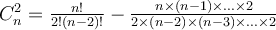 combinaisons de deux éléments parmi
n.
combinaisons de deux éléments parmi
n.
Après simplification, cela fait, 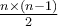 .
.
On voit donc que le coefficient de corrélation de Kendall représente en fait le degré auquel les deux variables sont rangées dans le même ordre. Il faut cependant noter que les ex aequo ne sont ni des paires concordantes, ni des paires discordantes et qu'il faut donc introduire un facteur de correction en cas d'ex aequo.
2. Liaison entre deux variables nominales
Rappelons que les variables nominales sont des variables telles que leurs valeurs correspondent à des catégories discrètes mutuellement exclusives, mais qu'il n'existe pas de relation d'ordre entre ces modalités. On ne peut même pas les classer entre elles. Tout ce que l'on peut faire, c'est donc de compter combien d'individus tombent dans chaque modalité.
Dans ces conditions, comment peut-on évaluer la liaison entre deux variables ? Un premier élément de solution consiste à s'interroger sur ce que signifierait au contraire l'indépendance, l'idée étant que si l'on sait évaluer à quel degré des variables sont indépendantes, cela nous donne de facto une indication sur le degré auquel elles sont liées. Dans la grande leçon sur la Statistique descriptive, nous avons vu que des variables peuvent être considérées indépendantes si les valeurs prises par une variable ne sont pas affectées par les valeurs prises sur l'autre variable. Puisque, ici, nous travaillons avec des variables nominales, cela revient à dire que la distribution des effectifs dans les modalités d'une variable ne sera pas affectée par la distribution des effectifs dans l'autre variable. C'est l'idée sous-jacente au  .
.
A. Le Khi-2 d'indépendance (ou Khi-deux, ou Chi-2, ou encore  ).
).
À titre d'exemple, commençons par considérer deux variables nominales dichotomiques, une variable Sexe avec deux modalités, Homme et Femme, et une variable Salaire à deux modalités, haut salaire et bas salaire. On s'intéresse à savoir s'il y a un lien entre le sexe et le salaire. On a un échantillon de sujets, et le tri croisé donne le tableau de données suivant :
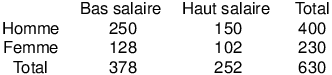
La première chose que nous remarquons en regardant les marges du tableau, c'est-à-dire la colonne Total et la ligne Total, c'est que dans cet échantillon, la proportion des femmes est plus faible que la proportion des hommes. Par ailleurs, nous voyons aisément que la proportion des bas salaires est plus importante que celle des hauts salaires. Seulement voilà, il ne s'agit là que de considérations relatives chacune à une variable prise isolément, sans considération de l'autre variable. Or, ce qui nous intéresse, c'est de comprendre la liaison éventuelle entre les variables, donc de considérer les deux variables SIMULTANÉMENT.
Ce sont les cellules à l'intérieur du tableau qui nous donnent ces informations. Ainsi, par exemple, la case à l'intersection de la colonne 1 et de la ligne 1, nous renseigne sur les hommes ayant un bas salaire. Il va donc falloir comparer l'effectif observé dans cette case avec l'effectif théorique qu'on aurait en cas d'indépendance des deux variables.
Comment obtenir l'effectif théorique ? Pour traiter cette question, nous allons considérer que les marges du tableau nous donnent des informations sur les taux de base, c'est-à-dire les distributions de fréquences a priori de notre échantillon. Pour calculer l'effectif théorique de la case "Hommes à bas salaires", il nous suffit alors de multiplier le nombre total d'hommes (case Total de la ligne 1) par le nombre total de personnes à bas salaires (case Total de la colonne 1), puis à diviser le résultat par l'effectif général (ici le contenu de la case en bas à droite, soit 630) pour que la somme des effectifs théoriques des quatre cases, donne un effectif théorique total qui soit identique à l'effectif observé.
Autrement dit, dans le cas général, en notant
Li
le total de la ligne
i
et
Ci
le total de la colonne
j, l'effectif théorique de la cellule
ij
est donné par la formule
Cela nous donne alors le tableau des effectifs théoriques :
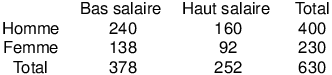
Pour chaque case, nous sommes alors en mesure de calculer les écarts à la valeur théorique en faisant simplement la différence entre les cellules correspondantes. Par exemple, dans la case hommes à bas salaires, nous avons observé 250 sujets alors que les effectifs théoriques n'étaient que de 240. Autrement dit, nous avons un écart de +10 pour cette case : nous observons 10 hommes à bas salaires de plus que ce que nous aurions attendu sous l'hypothèse d'indépendance des variables.
Afin d'éviter les compensations, on élève chaque différence au carré. Il paraît cependant clair que la signification d'une sur-représentation (il y a plus d'individus qu'attendu théoriquement) ou d'une sous-représentation (il y a moins d'individus qu'attendu théoriquement) est à relativiser en fonction de l'effectif théorique de la case : Le même écart de 10 sujets n'a pas le même sens selon qu'on attendait 20 ou 3000 sujets dans la case. On divisera donc le carré de l'écart par l'effectif théorique afin d'obtenir un carré pondéré de l'écart.
Il ne reste alors qu'à sommer les carrés pondérés des écarts obtenus dans chaque case pour obtenir le  . Ainsi, dans le cas général où la variable en ligne a
L
modalités et la variable en colonne a
C
modalités, et en notant
oij
l'effectif observé d'une case à l'intersection de la ligne
i
et de la colonne
j, et
tij
son effectif théorique, nous obtenons la formule
. Ainsi, dans le cas général où la variable en ligne a
L
modalités et la variable en colonne a
C
modalités, et en notant
oij
l'effectif observé d'une case à l'intersection de la ligne
i
et de la colonne
j, et
tij
son effectif théorique, nous obtenons la formule
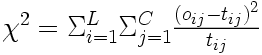
Dans l'exemple précédent, cela nous donne donc  =0,42+0,63+0,72+1,09 = 2,85.
=0,42+0,63+0,72+1,09 = 2,85.
On voit donc immédiatement que le  peut dépasser 1. Il suffit aussi de considérer la formule pour se persuader qu'il ne saurait être négatif. Le
peut dépasser 1. Il suffit aussi de considérer la formule pour se persuader qu'il ne saurait être négatif. Le  ne peut donc pas être assimilé à un coefficient de corrélation. En fait, comme nous l'avons dit dans l'article sur les distributions, la variable
ne peut donc pas être assimilé à un coefficient de corrélation. En fait, comme nous l'avons dit dans l'article sur les distributions, la variable  suit une distribution particulière et c'est l'application de techniques statistiques fondées sur cette distribution qui nous permet ensuite de décider si l'hypothèse d'indépendance est plausible ou doit être rejetée.
suit une distribution particulière et c'est l'application de techniques statistiques fondées sur cette distribution qui nous permet ensuite de décider si l'hypothèse d'indépendance est plausible ou doit être rejetée.
Il faut noter que l'utilisation du  est déconseillée lorsque l'effectif théorique de certaines cases est petit (plus petit que 5). Il faut donc disposer d'autres indices.
est déconseillée lorsque l'effectif théorique de certaines cases est petit (plus petit que 5). Il faut donc disposer d'autres indices.
B. L'indice Phi ( )
)
C'est un indice d'association que l'on rencontre fréquemment dans la littérature, dès lors que les deux variables sont dichotomiques (elles n'ont chacune que deux modalités). Sa formule est la suivante et se calcule à partir du  :
:
Notons qu'une autre façon d'obtenir le coefficient  consiste à recoder chaque variable en 0 et 1, puis à calculer un simple coefficient de corrélation de Pearson sur ces variables recodées, ce qui montre bien la similarité de nature entre le coefficient
consiste à recoder chaque variable en 0 et 1, puis à calculer un simple coefficient de corrélation de Pearson sur ces variables recodées, ce qui montre bien la similarité de nature entre le coefficient  et une corrélation.
et une corrélation.
C. L'indice V de Cramér
Le V de Cramér est une généralisation du coefficient  qui permet de traiter les cas où il y a plus de deux modalités. On commence alors par calculer la valeur
qui permet de traiter les cas où il y a plus de deux modalités. On commence alors par calculer la valeur 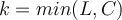 , où la fonction min consiste représente un minimum.
, où la fonction min consiste représente un minimum.
Autrement dit, on prend pour k la plus petite des deux valeurs
L
et
C, c'est-à-dire, selon la convention vue plus haut, le nombre de lignes
L
ou le nombre de colonnes
C. L'indice
V
est alors donné par 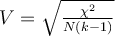 .
.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte