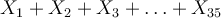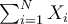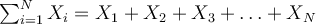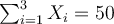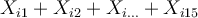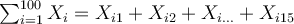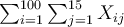Somme algébrique
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L1 |
| Livre: | Somme algébrique |
| Imprimé par: | Visiteur anonyme |
| Date: | jeudi 5 mars 2026, 06:57 |
Description
Objectifs. Rappeler la construction et la signification de l'opérateur de sommation discrète, utilisé dans de très nombreuses formules de statistique et psychométrie.
Prérequis. Aucun.
Résumé. La somme simple, d'abord présentée, est ensuite étendue à la somme double.
rédaction : Éric Raufaste
1. La somme simple
1. La somme simple
Tout le monde connaît l'opération d'addition. Supposons que l'on souhaite calculer la somme des notes en poésie obtenues par les 35 élèves d'une classe en vue de calculer ensuite la moyenne de la classe. Si l'on note X i la note obtenue par le ième élève de la classe, cette somme pourrait naturellement s'écrire
On dénote usuellement une somme d'éléments par la lettre grecque sigma majuscule : 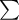 . Cela nous donne donc la formule suivante :
. Cela nous donne donc la formule suivante :
Mais imaginons qu'il y ait maintenant dix mille nombres à sommer, cette notation serait peu pratique. Une première idée consiste à imaginer que cette somme est une répétition de la même opération pour chacune des observations à sommer. Ainsi, pour chaque observation, j'ajoute à mon résultat intermédiaire la nouvelle valeur à ajouter et le résultat final est obtenu lorsque j'ai ajouté la dernière valeur. On peut alors désigner chaque élément à ajouter par un indice qui augmente progressivement de 1 en 1 en partant de 1, soit 1, 2, 3, etc. jusqu'à
N, le nombre d'observations. Notons
i
un tel indice. On pourra dès lors dire que 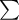 est la somme des nombres
est la somme des nombres 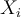 pour
i
variant de 1 à
N.
pour
i
variant de 1 à
N.
Afin d'illustrer le propos, voyons ce que cela donne sur un exemple concret dans lequel on cherche à sommer les nombres de l'ensemble suivant {12 ; 15 ; 23}. On a donc trois nombres (N
=3), 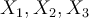 , et on a
, et on a 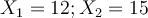 et enfin
et enfin
 . Je pars d'un total intermédiaire initialement à 0 et un indice
i
qui vaut initialement 1. La valeur correspondante est alors
. Je pars d'un total intermédiaire initialement à 0 et un indice
i
qui vaut initialement 1. La valeur correspondante est alors 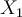 , soit 12. J'ajoute donc 12 à mon total intermédiaire qui vaut maintenant 0+12=12. Comme
i
est plus petit que
N, j'augmente
i
qui passe à 2. La valeur correspondante est alors
, soit 12. J'ajoute donc 12 à mon total intermédiaire qui vaut maintenant 0+12=12. Comme
i
est plus petit que
N, j'augmente
i
qui passe à 2. La valeur correspondante est alors 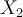 , soit 15. J'ajoute donc 15 à mon résultat intermédiaire qui vaut maintenant 15+12=27. Puisque
i
est encore plus petit que
N
, j'augmente
i
qui passe à 3. La valeur correspondante est alors
, soit 15. J'ajoute donc 15 à mon résultat intermédiaire qui vaut maintenant 15+12=27. Puisque
i
est encore plus petit que
N
, j'augmente
i
qui passe à 3. La valeur correspondante est alors 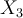 , soit 23. J'ajoute donc 23 à mon précédent résultat intermédiaire qui passe donc maintenant à 27+23=50. Arrivé là,
i
est égal à
N
et donc j'ai fini toutes mes additions.
, soit 23. J'ajoute donc 23 à mon précédent résultat intermédiaire qui passe donc maintenant à 27+23=50. Arrivé là,
i
est égal à
N
et donc j'ai fini toutes mes additions.
Finalement, on en arrive à écrire notre somme dans le cas général de la façon suivante :
Et l'on a
2. La somme double
Imaginons que l'on ait à faire pour chaque sujet une somme des notes qu'il a obtenues à chacune de 15 épreuves. Puis que nous ayons besoin de calculer la somme des notes obtenues par l'ensemble des 100 sujets d'une expérience. Nous avons donc deux sommes emboîtées l'une dans l'autre.
Si nous considérons nos données, en indiçant chaque valeur par le numéro de sujet et le numéro de note pour le sujet 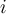 considéré, nous avons pour le sujet n°1 quelque chose comme
considéré, nous avons pour le sujet n°1 quelque chose comme
Pour le sujet n°2,
Jusqu'au sujet n°100 où cela devient complètement illisible,
Essayons donc de trouver une écriture plus lisible et plus dense. Afin d'obtenir une écriture un peu plus générale, nous pouvons variabiliser le numéro de sujet (i.e., le remplacer par une variable, disons ici une variable
i
qui variera de 1 à 100). Nous pouvons alors décrire une ligne de numéro
i
quelconque par la formule,
Puisque, à la page précédente, nous avons vu qu'il était possible de simplifier l'écriture avec l'opérateur de sommation, nous pouvons écrire  la somme sur les 100 sujets, soit
la somme sur les 100 sujets, soit
Cela reste assez lourd. Mais rien ne nous empêche de variabiliser aussi le numéro d'épreuve, par exemple en utilisant la variable
j, qui variera de 1 à 15 selon les 15 épreuves, puis d'appliquer une deuxième fois l'opérateur de sommation, à l'intérieur de chaque sujet. D'où la formule suivante, bien plus élégante puisqu'elle résume à elle seule toutes les opérations réalisées sur tous les sujets :
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte