Savoir trouver les valeurs critiques du t de student
Interpréter des résultats de t de student à échantillons appariés
Interpréter les sorties d'un test t à 2 échantillons indépendants réalisé sous R (version 2.12)
Ayant procédé au test sous R 2.12.1 (nous partons ici de l'idée que le test a été lancé à partir du package RCmdr, menu "Statistiques/Moyennes/t test univarié"), notre chercheur obtient le tableau de résultats suivant :
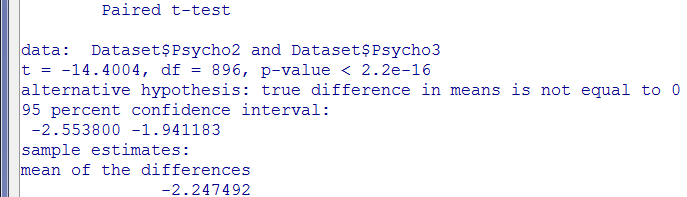
Explication des lignes de résultats
Paired t-test :
C'est le nom anglais de la procédure, littéralement "test t apparié"
Data : Dataset$Psycho3 and Dataset$Psycho2
Le fichier de données ayant été chargé dans une table qui s'appelle "Dataset", on compare les deux variables "Psycho3" et "Psycho2" de ce tableau
t = 14.4004, df = 896, p-value < 2.2e-16
t : C'est tout simplement la valeur du t de student, 14.4004 arrondie à la quatrième décimale
df : abbréviation anglaise de "degrees of freedom". C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons appariés, le nombre de sujets moins 1, soit 896.
p-value : C'est la valeur du risque de type 1 ou risque alpha, la valeur
p. Ici, en notation scientifique, soit 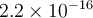 , donc en fait très largement en dessous du seuil de signification...
, donc en fait très largement en dessous du seuil de signification...
alternative hypothesis: true difference in means is not equal to 0 : l'hypothèse alternative à l'hypothèse nulle est qu'il existe véritablement (i.e., non due au hasard) une différence non nulle entre les moyennes.
95 percent confidence interval:
1.941183 2.553800
Il y a 95% de chances que la vraie valeur de la moyenne des différences entre ces deux variables soient comprise dans cet intervalle.
sample estimates:
mean of the differences
2.247492
Valeur moyenne des différences entre les deux variables.
Comment rapporter les résultats
Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.
Ici, nous imaginerons le cas de résultats rapportés dans un texte qui suit les normes APA 7e édition.
Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :
"La moyenne des résultats à l'épreuve Psycho2 est M2 =11.50 (SD = 4.33) alors que celle des femmes est M3 =13.75 (SD = 3.59). La moyenne des notes à Psycho3 est significativement plus forte t(896) = 14.4, p <.001".
En fait, on doit écrire p<.001 car, si l'on regarde la valeur du p calculé avec plus de décimales (ce qui n'apparaît pas sur l'image ci-dessus), on constate que la valeur de p est extrêmement proche de 0, et en tout cas inférieure à .001.
Couleur de fond
Police
Taille de police
Couleur de texte