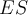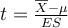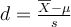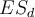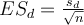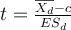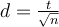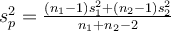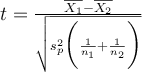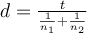Imprimer tout le livreImprimer tout le livre

t de student : Interpréter les sorties des logiciels SPSS 18, Statistica 8, R

Site: IRIS - Les cours en ligne de l'UT2J
Cours: UOH / Statistique et Psychométrie en L2
Livre: t de student : Interpréter les sorties des logiciels SPSS 18, Statistica 8, R
Imprimé par: Visiteur anonyme
Date: mercredi 8 mai 2024, 23:51

Description

C'est une chose de réaliser un test avec un logiciel, c'est-à-dire lui fournir des données et lui faire produire les valeurs t et p, c'est en une autre de savoir interpréter les sorties du logiciel.
Cette section présente les interprétations de sorties de différents logiciels pour...

  • test t à échantillon unique
  • test t à groupes appariés
  • test t à groupes indépendants

Logiciels considérés : Jamovi, R, SPSS, Statistica, Tableurs


Table des matières

1. Interpréter des résultats de test t à échantillons indépendants

Objectifs. Sur la base d'un exemple, mettre l'étudiant en position de interpréter des sorties logicielles de test t à échantillons indépendants.

Prérequis.

Résumé. Après une brève présentation du fichier de données, de l'hypothèse opérationnelle et du test réalisé, on montre la sortie de trois logiciels de statistiques différents (Statistica 8, SPSS 18, R). On expose comment interpréter ces sorties et comment présenter les résultats aux normes internationales en vigueur en psychologie (APA 7th edition)

1.1. Introduction : le fichier de données et l'hypothèse testée dans les exemples

Contexte de l'étude

Lors d'un concours pour entrer dans une grande institution, 897 candidats ont été soumis à des tests psychotechniques et académiques. Le test permet d'obtenir des notes comprises entre 0 et 105. Idéalement, on voudrait que ce test ne fasse pas de discrimination entre les sexes. Le chercheur veut donc vérifier si les notes obtenues en moyennes au test "PSYCHO1" sont les mêmes pour les hommes et pour les femmes.

Description brève des données

Les données sont contenues dans un fichier (que vous pouvez télécharger ici au format texte tabulé). Lors d'un concours pour entrer dans une grande institution, 897  candidats ont été soumis à des tests psychotechniques et académiques. Pour ne pas désavantager les femmes, déjà nettement moins nombreuses à se présenter à ce type de concours, le chercheur veut comparer les moyennes des hommes et des femmes à l'épreuve "PSYCHO1", ceci afin de vérifier que les deux moyennes sont sensiblement identiques, faute de quoi on pourrait s'interroger sur la légitimité d'appliquer ce test en entrée d'un concours.

Le fichier contient 897 lignes, ayant chacune 8 variables :

  1. "Candidat" : le numéro du candidat "
  2. "Psycho1" : La note obtenue au tests psychotechnique PSYCHO1
  3. "Psycho2" : La note obtenue au tests psychotechnique PSYCHO2
  4. "Psycho3" : La note obtenue au tests psychotechnique PSYCHO3
  5.  "Sexe" : 1 si garçon, 2 si fille
  6. "Math" : La note obtenue en maths
  7. "Phys" : La note obtenue en physique
  8. "Langue" : La note obtenue en langue

Le test réalisé

Notre chercheur va donc comparer la moyenne des notes obtenues sur la variable "Psycho1" en fonction des valeurs de la variable Sexe (qui vaut "1" pour les hommes, "2" pour les femmes). Il va pour cela utiliser un test de student à groupes indépendants puisque chaque observation correspond à une personne unique, soit homme, soit femme.

1.2. Interpréter les sorties d'un test t à 2 échantillons indépendants réalisé sous Statistica 8

Ayant procédé au test sous Statistica 8, notre chercheur obtient le tableau de résultats suivant :



Explication des colonnes de données

Moyenne 1 : contient la moyenne de la variable Psycho1 pour les sujets dont la variable Sexe=1 (les hommes), ici m1 =67,07623.

Moyenne 2 : contient la moyenne de la variable Psycho1 pour les sujets dont la variable Sexe=2 (les femmes), ici m2 =69,0352.

Valeur t : C'est tout simplement la valeur du t de student arrondie à la 5^e décimale, obtenue en comparant les deux moyennes précédentes soit t =-1,65166. Le signe  négatif vient de ce que la différence (m1-m2) est négative.

dl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons indépendants, le nombre de sujets moins 2, soit 895.

p : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, arrondie à la sixième décimale, soit 0,098954. Comme cette valeur dépasse le seuil de 5%, soit .05, on considérera le test comme non significatif, et donc que la passation de l'épreuve ne discrimine pas les deux sexes. Cela étant, puisque cette valeur est < .10, on pourra la considérer comme "tendancielle" ou encore "marginalement significative". Peut-être faudrait-il regarder plus près dans l'épreuve quels sont les items qui différencient le plus les deux sexes et retirer ces items du test.

N actifs 1 : Il s'agit du nombre d'observations prises en compte dans la modalité 1 du facteur Sexe, ici 774.

N actifs 2 : Il s'agit du nombre d'observations prises en compte dans la modalité 1 du facteur Sexe, ici 123. On note que les femmes ont été nettement moins nombreuses que les hommes à se présenter au concours, une observation classique pour ce type de concours et une raison de plus pour veiller à ne pas les désavantager.

Écart-type 1 : Il s'agit de l'écart-type des 774 observations de la modalité 1 du facteur Sexe, soit 12,25835.

Écart-type 2 : Il s'agit de l'écart-type des 123 observations de la modalité 2 du facteur Sexe, soit 11,84042.

Ratio F Variances : il s'agit du test F utilisé pour vérifier si les variances des deux groupes sont égales. Ici la valeur du F est 1,071839.

p Variances : il s'agit de la valeur p du test F utilisé pour vérifier si les variances des deux groupes sont égales. Ici p=0.641576, ce qui est non significatif. On voit donc que les variances peuvent être considérées comme homogènes puisque leur différence peut être expliquée par un pur effet du hasard.

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans le texte, en utilisant les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des hommes à l'épreuve Psycho1 est 67.08 (SD = 12.26) alors que celle des femmes est 69.03 (SD =11.84). La différence, qui au demeurant est en faveur des femmes, n'est cependant que tendancielle t(895) = 1.65, p < .10 " et les variances peuvent être considérées comme homogènes."

On ne rapporte généralement pas les tests de signification pour l'homogénéité des variances, car si les variances ne sont pas homogènes, on applique généralement une variante du test t, le test de Welch.

Notez les italiques qui s'appliquent aux lettres représentant des symboles comme t ou p. Le test d'homogénéité des variances n'étant clairement pas significatif, nous nous sommes limités à énoncer le résultat. Veuillez noter aussi la précaution "peuvent être considérées comme homogènes". En effet, les accepter définitivement comme homogène reviendrait à dire que l'hypothèse nulle est vraie, ce que l'on ne doit fait jamais faire (car on ne peut en être certains).

1.3. Interpréter les sorties d'un test t à 2 échantillons indépendants réalisé sous SPSS 18

Ayant procédé au test sous SPSS 18, notre chercheur obtient le tableau de résultats suivant :


Explication des colonnes de données

On voit que le tableau contient deux lignes, une pour l'hypothèse de variances égales, et l'autre pour l'hypothèse de variances inégales. 

F : il s'agit du test F issu du test de Levene, utilisé pour vérifier si les variances des deux groupes sont égales ou non. Ici la valeur du F est 1,481.

Sig. : il s'agit de la valeur p du test de Levene précédent. Ici p=0.224, ce qui est non significatif. On voit donc que les variances peuvent être considérées comme homogènes puisque leur différence peut être expliquée par un pur effet du hasard. Il s'ensuit que pour la suite des résultats, nous devrons utiliser la ligne "Hypothèse de variances égales" plutôt que la ligne "hypothèse de variances inégales".

t : C'est tout simplement la valeur du t de student arrondie à la 3e décimale, obtenue en comparant les deux moyennes précédentes soit t =-1,652. Le signe - vient de ce que la différence (m1- m2) est négative. 

ddl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons indépendants, le nombre de sujets moins 2, soit 895.

Sig. (bilatérale) : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, arrondie à la troisième décimale, soit 0,098954. Comme cette valeur dépasse le seuil de 5%, soit 0,05, on considérera le test comme non significatif, et donc que la passation de l'épreuve ne discrimine pas les deux sexes. Cela étant, puisque cette valeur est <.10, on pourra la considérer comme tendancielle. Peut-être faudrait-il regarder plus près dans l'épreuve quels sont les items qui différencient le plus les deux sexes et retirer ces items du test. Si le test de Levene avait été significatif, on aurait utilisé la valeur indiquée sur la ligne du dessous.

Différence moyenne : contient la différence des moyennes de la variable Psycho1 pour les sujets dont la variable Sexe="1" (les hommes) et ceux dont la variable Sexe="2" (les femmes). ici -1,956.

Les autres colonnes ne sont généralement pas utiles au niveau visé par ce cours.

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans le texte, en utilisant les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des hommes à l'épreuve Psycho1 est 67.08 (SD = 12.26) alors que celle des femmes est 69.03 (SD =11.84). La différence, qui au demeurant est en faveur des femmes, n'est cependant que tendancielle t(895) = 1.65, p < .10 " et les variances peuvent être considérées comme homogènes."

On ne rapporte généralement pas les tests de signification pour l'homogénéité des variances, car si les variances ne sont pas homogènes, on applique généralement une variante du test t, le test de Welch.

Notez les italiques qui s'appliquent aux lettres représentant des symboles comme t ou p. Le test d'homogénéité des variances n'étant clairement pas significatif, nous nous sommes limités à énoncer le résultat. Veuillez noter aussi la précaution "peuvent être considérées comme homogènes". En effet, les accepter définitivement comme homogène reviendrait à dire que l'hypothèse nulle est vraie, ce que l'on ne doit fait jamais faire (car on ne peut en être certains).

1.4. Interpréter les sorties d'un test t à 2 échantillons indépendants réalisé sous R (version 2.12)

Ayant procédé au test sous R 2.12.1 (nous partons ici de l'idée que le test a été lancé à partir du package RCmdr, menu "Statistiques/Moyennes/t test univarié"), notre chercheur obtient le tableau de résultats suivant :

Explication des lignes de résultats

Two sample t-test :

C'est le nom anglais de la procédure, littéralement "test t à deux échantillons"

Data : Psycho1by Sexe

Rappel précisant qu'on a testé la variable Psycho1, en construisant des groupes basés sur les deux modalités de la variable Sexe

t = -1.6517, df = 895, p-value = 0.09895

t : C'est tout simplement la valeur du t de student, -1.6517 arrondie à la quatrième décimale

df : abbréviation anglaise de "degrees of freedom". C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons indépendants, le nombre de sujets moins 2, soit 895.

p-value : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, arrondie à la cinquième décimale, soit 0,09895. Comme cette valeur dépasse le seuil de 5%, soit 0,05, on considérera le test comme non significatif, et donc que la passation de l'épreuve ne discrimine pas les deux sexes. Cela étant, puisque cette valeur est <.10, on pourra la considérer comme tendancielle. Peut-être faudrait-il regarder plus près dans l'épreuve quels sont les items qui différencient le plus les deux sexes et retirer ces items du test.

alternative hypothesis: true difference in means is not equal to 0

L'hypothèse nulle d'une comparaison de moyennes représente l'égalité. Ici, on compare les moyennes de la variable Psycho1 obtenues pour les hommes et les femmes. Donc l'hypothèse nulle est que la moyenne de la différence est 0. Autrement dit que l'écart entre la valeur réelle de cette différence et 0 n'est du qu'à des effets aléatoires.

L'hypothèse alternative est que l'hypothèse est fausse et donc que la différence "réelle" (true difference en anglais) dans la population d'où est tiré l'échantillon n'est PAS égale à 0.

95 percent confidence interval:
-4.2808916 0.3683057

Il s'agit de l'intervalle de confiance à 95% de la différence des moyennes, les bornes inférieure et supérieure de l'intervalle calculé de manière à ce que la moyenne "réelle"de la population ait 95% de chance d'être contenue dedans.

sample estimates:
Mean in group Hommes  Mean in group Femmes
    67.07623                              69.03252

Il s'agit des estimations des moyennes réalisées à partir de l'échantillon arrondies à la cinquième décimale, pour les hommes et pour les femmes.

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans le texte, en utilisant les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des hommes à l'épreuve Psycho1 est 67.08 (SD = 12.26) alors que celle des femmes est 69.03 (SD =11.84). La différence, qui au demeurant est en faveur des femmes, n'est cependant que tendancielle t(895) = 1.65, p < .10 " et les variances peuvent être considérées comme homogènes."

On ne rapporte généralement pas les tests de signification pour l'homogénéité des variances, car si les variances ne sont pas homogènes, on applique généralement une variante du test t, le test de Welch.

Notez les italiques qui s'appliquent aux lettres représentant des symboles comme t ou p. Le test d'homogénéité des variances n'étant clairement pas significatif, nous nous sommes limités à énoncer le résultat. Veuillez noter aussi la précaution "peuvent être considérées comme homogènes". En effet, les accepter définitivement comme homogène reviendrait à dire que l'hypothèse nulle est vraie, ce que l'on ne doit fait jamais faire (car on ne peut en être certains).

2. Interpréter des résultats de test t à échantillon unique

Objectifs. Sur la base d'un exemple, mettre l'étudiant en position de interpréter des sorties de test t à échantillon unique.

Prérequis. Comparaisons de moyennes.

Résumé. Après une brève présentation du fichier de données, de l'hypothèse opérationnelle et du test réalisé, on montre la sortie de trois logiciels de statistiques différents (Statistica 8, SPSS 18, R). On expose comment interpréter ces sorties et comment présenter les résultats aux normes internationales en vigueur en psychologie (APA 6th edition)

2.1. Introduction : le fichier de données et l'hypothèse testée dans les exemples

Contexte de l'étude

Lors d'un concours pour entrer dans une grande institution, 897 candidats ont été soumis à des tests psychotechniques et académiques. Le test permet d'obtenir des notes comprises entre 0 et 105. Typiquement, la moyenne des candidats sur ce test devrait être autour de 52,5. Le chercheur veut vérifier que les notes obtenues en moyennes au test "PSYCHO1" ne s'écartent pas trop de la valeur de référence, 52,5, pour qu'on puisse considérer que le test est bien applicable à la population considérée.

Description brève des données

Les données sont contenues dans un fichier (que vous pouvez télécharger ici au format texte tabulé). Lors d'un concours pour entrer dans une grande institution, 897  candidats ont été soumis à des tests psychotechniques et académiques. Le chercheur veut vérifier que les notes obtenues en moyennes au test "PSYCHO1" ne s'écartent pas trop de la valeur de référence qu'il possède pour qu'on puisse considérer que le test est applicable à la population considérée.

Le fichier contient 897 lignes, ayant chacune 8 variables :

  • "Candidat" : le numéro du candidat "
  • "Psycho1" : La note obtenue au test psychotechnique PSYCHO1
  • "Psycho2" : La note obtenue au test psychotechnique PSYCHO2
  • "Psycho3" : La note obtenue au test psychotechnique PSYCHO3
  •  "Sexe" : 1 si garçon, 2 si fille
  • "Math" : La note obtenue en maths
  • "Phys" : La note obtenue en physique
  • "Langue" : La note obtenue en langue

Le test réalisé

Notre chercheur va donc comparer la moyenne des notes obtenues sur la variable "Psycho1" et va la comparer à la note de référence,66, au moyen d'un test t de student.

2.2. Interpréter les sorties d'un test de moyenne à échantillon unique réalisé sous Statistica 8

Ayant procédé au test sous Statistica 8, notre chercheur obtient le tableau de résultats suivant :

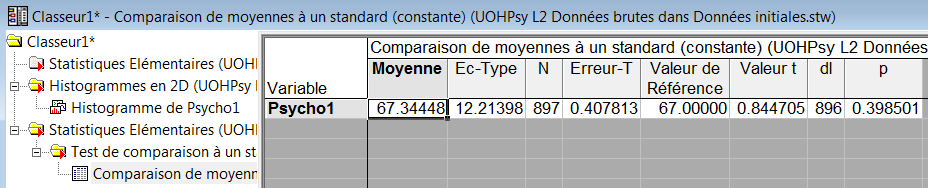
La partie gauche de l'image contient la liste des tableaux de résultats. Ici, c'est la ligne "Comparaison de moyennes qui est sélectionnée. La partie droite de l'image affiche les résultats correspondant à la comparaison de moyenne.

Explication des colonnes de données

Moyenne : contient la moyenne de la variable Psycho1, ici 67,3448.

EC-Type : Il s'agit de l'écart-type de la variable Psycho1, ici 12,21398.

N : Il s'agit du nombre d'observations prises en compte, ici 897. Si, parmi les 897 candidats, certains n'avaient pas passé ce test et que le fichier ne contienne aucune valeur pour ces candidats, N aurait été plus petit que 897.

Erreur-Type : Ce nombre est utilisé pour calculer les intervalles de confiance ou pour des calculs intermédiaires. Il correspond à l'écart-type divisé par la racine carré de N (donc ici 67,3448 / racine(897) = 0,407813.

Valeur de référence : Il s'agit de la constante contre laquelle a été testée la moyenne des candidats. Ici 67.

Valeur t : C'est tout simplement la valeur du t de student, 0.844705

dl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillon unique, le nombre de sujets moins 1, soit 896.

p : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, arrondie à la sixième décimale, soit 0,398501. Comme cette valeur dépasse le seuil de 5%, soit 0,05, le risque pris en rejetant l'hypothèse nulle est beaucoup trop grand. On considérera donc que le test est non significatif, et donc que la passation de l'épreuve Psycho1 n'est pas fondamentalement différente des conditions pour lesquelles elle a été prévue. On pourra donc utiliser cette épreuve (sous réserve que les autres précautions méthodologiques d'usage aient été respectées bien sûr).

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans le texte en utilisant les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne de l'échantillon au test Psycho1 est 67.34 (SD =12.21), et cette valeur n'est pas statistiquement différente de la valeur de référence du test, à savoir 67, t(896) = 0.84, p=.399."

Notez les italiques qui s'appliquent aux lettres représentant des symboles comme t ou p.

2.3. Interpréter les sorties d'un test de moyenne à échantillon unique réalisé sous SPSS 18

Ayant procédé au test sous SPSS 18, notre chercheur obtient le tableau de résultats suivant :

Sur les résultats complets, la partie gauche de l'image contient la liste des tableaux de résultats.Ici nous avons isolé la partie droite correspondant à notre comparaison de moyenne.

Explication des colonnes de données du tableau "Statistiques sur échantillon unique"

t : C'est tout simplement la valeur du t de student, 0,845 (arrondi du 0.844705 qu'on avait sous Statistica). Notez qu'il est possible de double-cliquer dans le tableau SPSS pour faire apparaître plus de décimales. Notez aussi que le 0 avant la virgule n'est pas affiché, ce qui est un abus puisque les valeurs de t peuvent dépasser 1.

N : Il s'agit du nombre d'observations prises en compte, ici 897. Si, parmi les 897 candidats, certains n'avaient pas passé ce test et que le fichier ne contienne aucune valeur pour ces candidats, N aurait été plus petit que 897. 

Moyenne : contient la moyenne de la variable Psycho1, ici 67,34.

Ecart-type : Il s'agit de l'écart-type de la variable Psycho1, ici 12,214.

Erreur standard moyenne : Ce nombre est utilisé pour calculer les intervalles de confiance ou pour des calculs intermédiaires. Il correspond à l'écart-type divisé par la racine carré de N (donc ici 67,3448 / racine(897) = 0,408.

Explication des colonnes de données du tableau "Test sur échantillon unique"

Notez que la valeur de référence de 67, la constante contre laquelle a été testée la moyenne des candidats, est indiquée sur la première ligne du tableau avec l'intitulé "valeur du test = 67":

t : C'est la valeur du t de student arrondie à la troisième décimale, 0,845

ddl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillon unique, le nombre d'observations N moins 1, soit 896.

Sig (bilatérale) : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p . Ici, arrondie à la troisième décimale, soit 0,399. Comme cette valeur dépasse le seuil de 5%, soit 0,05, le risque pris en rejetant l'hypothèse nulle est beaucoup trop grand. On considérera donc que le test est non significatif, et donc que la passation de l'épreuve Psycho1 n'est pas fondamentalement différente des conditions pour lesquelles elle a été prévue. On pourra donc utiliser cette épreuve (sous réserve que les autres précautions méthodologiques d'usage aient été respectées bien sûr).

Différence moyenne : C'est différence entre la moyenne de la variable testée, Psycho1, soit 63.34 (arrondie à la deuxième décimale) et la valeur de référence, 67. Ici la différence est arrondie à la troisième décimale, soit 0,344.

Intervalle de confiance 95% de la différence : Les bornes inférieure et supérieure de l'intervalle calculé de manière à ce que la valeur réelle de la différence ait 95% de chance d'être contenue dedans. Ou encore, calculé de telle façon que 95 des sujets présentent un score compris dans cet intervalle.

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans le texte en utilisant les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne de l'échantillon au test Psycho1 est 67.34 (SD =12.21), et cette valeur n'est pas statistiquement différente de la valeur de référence du test, à savoir 67, t(896) = 0.84, p=.399."

Notez les italiques qui s'appliquent aux lettres représentant des symboles comme t ou p.

2.4. Interpréter les sorties d'un test de moyenne à échantillon unique réalisé sous R (version 2.12)

Ayant procédé au test sous R 2.12.1 (nous partons ici de l'idée que le test a été lancé à partir du package RCmdr, menu "Statistiques/Moyennes/t test univarié"), notre chercheur obtient le tableau de résultats suivant :

Explication des lignes de résultats

One sample t-test :

C'est le nom anglais de la procédure, littéralement "test t à un échantillon"

Data : Dataset$Psycho1

Rappel précisant que le fichier de données ayant été chargé dans la variable globale nommée Dataset, on a testé la variable Psycho1

t = 0.8447, df = 896, p-value = 0.3985

t : C'est tout simplement la valeur du t de student, 0,8447 (arrondi du 0.844705 qu'on avait sous Statistica).

df : abbréviation anglaise de "degrees of freedom". C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillon unique, le nombre d'observations N moins 1, soit 896.

p-value : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p .Ici, arrondie à la quatrième décimale, soit 0,3985. Comme cette valeur dépasse le seuil de 5%, soit 0,05, le risque pris en rejetant l'hypothèse nulle est beaucoup trop grand. On considérera donc que le test est non significatif, et donc que la passation de l'épreuve Psycho1 n'est pas fondamentalement différente des conditions pour lesquelles elle a été prévue. On pourra donc utiliser cette épreuve (sous réserve que les autres précautions méthodologiques d'usage aient été respectées bien sûr).

alternative hypothesis: true mean is not equal to 67

L'hypothèse nulle d'une comparaison de moyenne représente l'égalité. Ici on compare la moyenne de la variable Psycho1 et une valeur de référence 67. Donc l'hypothèse nulle est que la moyenne de Psycho1 = 67. Et que l'écart entre la valeur réelle de cette moyenne et 67 n'est du qu'à des effets aléatoires.

L'hypothèse alternative est que l'hypothèse est fausse et donc que la "moyenne réelle" (true mean en anglais) de la population d'où est tiré l'échantillon n'est PAS égale à 67.

95 percent confidence interval:
 66.54410 68.14486

Il s'agit de l'intervalle de confiance à 95% de la moyenne de la variable Psycho1 : Les bornes inférieure et supérieure de l'intervalle calculé de manière à ce que la moyenne "réelle"de la population ait 95% de chance d'être contenue dedans. Ou encore, calculé  de telle façon que 95 des sujets présentent un score compris dans cet intervalle.  

sample estimates:
mean of x
 67.34448

Il s'agit des estimations réalisées à partir de l'échantillon.

Mean of x est la moyenne de la variable Psycho1 arrondie à la cinquième décimale, soit 67.34448


Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans le texte en utilisant les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne de l'échantillon au test Psycho1 est 67.34 (SD =12.21), et cette valeur n'est pas statistiquement différente de la valeur de référence du test, à savoir 67, t(896) = 0.84, p=.399."

Notez les italiques qui s'appliquent aux lettres représentant des symboles comme t ou p.

3. Interpréter des résultats de t de student à échantillons appariés

Objectifs. Sur la base d'un exemple, mettre l'étudiant en position d'interpréter des sorties logicielles de test t à échantillons appariés.

Prérequis.

Résumé. Après une brève présentation du fichier de données, de l'hypothèse opérationnelle et du test réalisé, on montre la sortie de trois logiciels de statistiques différents (Statistica 8, SPSS 18, R). On expose comment interpréter ces sorties et comment présenter les résultats aux normes internationales en vigueur en psychologie (APA 7e édition)

3.1. Introduction : le fichier de données et l'hypothèse testée dans les exemples

Contexte de l'étude

Lors d'un concours pour entrer dans une grande institution, 897 candidats ont été soumis à des tests psychotechniques et académiques. Deux épreuves, "Psycho1" et "Psycho2", permettent d'obtenir des notes comprises entre 0 et 26. Le chercheur veut vérifier si une des deux épreuves peut être considérée comme plus difficile que l'autre. Il compare donc les notes obtenues par chaque sujet aux épreuves "Psycho2" et "Psycho3".

Description brève des données

Les données sont contenues dans un fichier (que vous pouvez télécharger ici au format texte tabulé). Lors d'un concours pour entrer dans une grande institution, 897  candidats ont été soumis à des tests psychotechniques et académiques.

Le fichier contient 897 lignes, ayant chacune 8 variables :

  • "Candidat" : le numéro du candidat "
  • "Psycho1" : La note obtenue au test psychotechnique PSYCHO1
  • "Psycho2" : La note obtenue au test psychotechnique PSYCHO2
  • "Psycho3" : La note obtenue au test psychotechnique PSYCHO3
  •  "Sexe" : 1 si garçon, 2 si fille
  • "Math" : La note obtenue en maths
  • "Phys" : La note obtenue en physique
  • "Langue" : La note obtenue en langue

Le test réalisé

Notre chercheur va donc comparer la moyenne des notes obtenues sur la variable "Psycho2" avec les notes obtenues sur la variable "Psycho3". Il va pour cela utiliser un test de student à groupes appariés puisque chaque sujet a fait l'objet d'une mesure les deux tests.

3.2. Interpréter les sorties d'un test t à 2 échantillons appariés réalisé sous Statistica 8

Ayant procédé au test sous Statistica 8, notre chercheur obtient le tableau de résultats suivant :

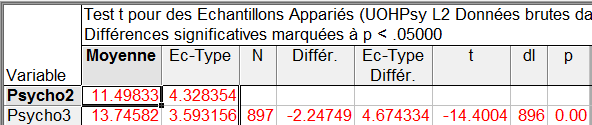
Explication des colonnes de données

La ligne 1 ne contient que les données descriptives de la variable Psycho2. La ligne 2 contient les données descriptives de la variable Psycho3 puis les données de statistique inférentielle. Les cellules en rouge correspondent aux tests significatifs, ce qui est le cas ici.

Moyenne : contient la moyenne des variables, ici 11.19833 pour Psycho 2 et 13,74582 pour Psycho3.

Ec-type : Il s'agit de l'écart-type des variables, ici 4.328354 pour Psycho 2 et 3,593156 pour Psycho3.

N : Il s'agit du nombre d'observations prises en compte, soit 897 observations pour lesquelles les deux variables sont renseignées.

Différ. : contient la moyenne des différences observées entre la variable 1 et la variable 2, ici -2.24749

Ec-type Différ. : Il s'agit de l'écart-type de l'échantillon constitué des différences entre Psycho2 et Psycho3 pour chaque sujet, soit 4,674334. 

t : C'est tout simplement la valeur du t de student arrondie à la 4e décimale, soit t =-14.4004. Le signe négatif vient de ce que la différence (Psycho2- Psycho3) est négative.

dl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons indépendants, le nombre de sujets moins 1, soit 896.

p : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, arrondie à la deuxième décimale, soit 0.00. Comme cette valeur est inférieure au de 5%, soit .05, on considérera le test comme significatif, et donc que l'épreuve 2 donne lieu à des notes significativement plus élevées que l'épreuve 3. Autrement, l'épreuve 3 semble plus difficile que l'épreuve 2. 

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans un texte qui suit les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des résultats à l'épreuve Psycho2 est M2 =11.50 (SD = 4.33) alors que celle des femmes est M3 =13.75 (SD = 3.59). La moyenne des notes à Psycho3 est significativement plus forte t(896) = 14.4, p <.001".

En fait, on doit écrire p<.001 car, si l'on regarde la valeur du p calculé avec plus de décimales (ce qui n'apparaît pas sur l'image ci-dessus), on constate que la valeur de p est extrêmement proche de 0, et en tout cas inférieure à .001.

3.3. Interpréter les sorties d'un test t à 2 échantillons appariés réalisé sous SPSS 18

Ayant procédé au test sous SPSS 18, notre chercheur obtient le tableau de résultats suivant :

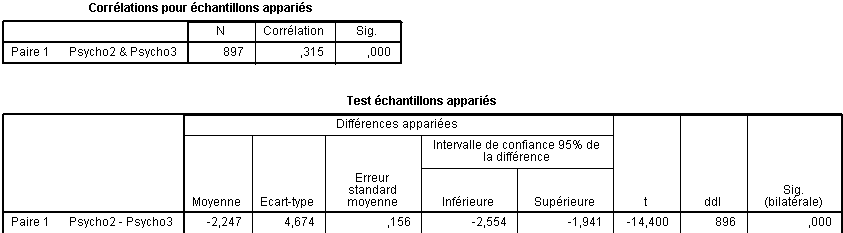
S_8_31.png

Tableau "Corrélations pour échantillons appariés"

 Ce tableau rapporte la corrélation qui existe entre les deux variables, ce qui est une donnée intéressante pour les calculs de tailles d'effet (qui ne sont pas dans ce cours) et qui renseigne aussi sur le degré de liaison entre les deux variables.

Ici le R de Pearson vaut 0,315 ce qui pour 897 couples de données est largement significatif ? Si l'on doit présenter cette corrélation dans le texte, on écrira " r (896)=.315, p <.001". Notez r (896) et non r (897), le nombre entre parenthèses représentant le nombre de degrés de liberté de la comparaison et non le nombre de couples.

Explication des colonnes de données du Tableau "Test échantillons appariés"

Moyenne : contient la moyenne des différences Psycho2-Psycho3, ici -2,247.

Ecart-type : Il s'agit de l'écart-type des différences Psycho2-Psycho3, ici 4,674.

Erreur standard moyenne : Ce nombre est utilisé pour calculer les intervalles de confiance ou pour des calculs intermédiaires. Il correspond à l'écart-type divisé par la racine carrée de N (donc ici 4,674 / racine(897) = 0,156. 

t : C'est tout simplement la valeur du t de student arrondie à la 3e décimale, obtenue en comparant les deux moyennes précédentes soit t =-14,400. Le signe "-" vient de ce que la différence (m1- m2) est négative. 

ddl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons indépendants, le nombre de sujets moins 1, soit 896.

Sig. (bilatérale) : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, tronquée à la troisième décimale, soit 0,000. Comme cette valeur est inférieure au seuil de 5%, soit 0,05, on considérera le test comme significatif et on peut donc dire que les notes Psycho3 sont significativement supérieures aux notes Psycho2.

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans un texte qui suit les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des résultats à l'épreuve Psycho2 est M2 =11.50 (SD = 4.33) alors que celle des femmes est M3 =13.75 (SD = 3.59). La moyenne des notes à Psycho3 est significativement plus forte t(896) = 14.44, p <.001".

En fait, on doit écrire p<.001 car, si l'on regarde la valeur du p calculé avec plus de décimales (ce qui n'apparaît pas sur l'image ci-dessus), on constate que la valeur de p est extrêmement proche de 0, et en tout cas inférieure à .001.

3.4. Interpréter les sorties d'un test t à 2 échantillons indépendants réalisé sous R (version 2.12)

Ayant procédé au test sous R 2.12.1 (nous partons ici de l'idée que le test a été lancé à partir du package RCmdr, menu "Statistiques/Moyennes/t test univarié"), notre chercheur obtient le tableau de résultats suivant :

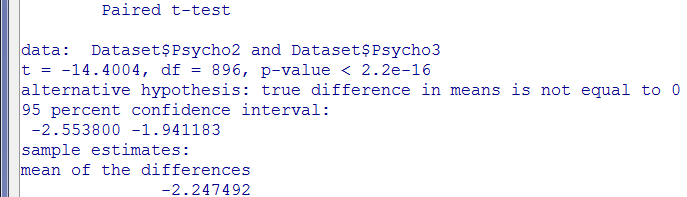
Explication des lignes de résultats

Paired t-test :

C'est le nom anglais de la procédure, littéralement "test t apparié"

Data : Dataset$Psycho3 and Dataset$Psycho2

Le fichier de données ayant été chargé dans une table qui s'appelle "Dataset", on compare les deux variables "Psycho3" et "Psycho2" de ce tableau

t = 14.4004, df = 896, p-value < 2.2e-16

t : C'est tout simplement la valeur du t de student, 14.4004 arrondie à la quatrième décimale  

df : abbréviation anglaise de "degrees of freedom". C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons appariés, le nombre de sujets moins 1, soit 896.

p-value : C'est la valeur du risque de type 1 ou risque alpha, la valeur p. Ici, en notation scientifique, soit 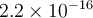2.2\times 10^{-16}, donc en fait très largement en dessous du seuil de signification...

alternative hypothesis: true difference in means is not equal to 0 : l'hypothèse alternative à l'hypothèse nulle est qu'il existe véritablement (i.e., non due au hasard) une différence non nulle entre les moyennes.

95 percent confidence interval:
      1.941183 2.553800

Il y a 95% de chances que la vraie valeur de la moyenne des différences entre ces deux variables soient comprise dans cet intervalle.

sample estimates:
mean of the differences
               2.247492
Valeur moyenne des différences entre les deux variables.

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans un texte qui suit les normes APA 7e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des résultats à l'épreuve Psycho2 est M2 =11.50 (SD = 4.33) alors que celle des femmes est M3 =13.75 (SD = 3.59). La moyenne des notes à Psycho3 est significativement plus forte t(896) = 14.4, p <.001".

En fait, on doit écrire p<.001 car, si l'on regarde la valeur du p calculé avec plus de décimales (ce qui n'apparaît pas sur l'image ci-dessus), on constate que la valeur de p est extrêmement proche de 0, et en tout cas inférieure à .001.

4. Formulaire Student

Avertissement : les formules présentées ici peuvent être sensiblement différentes en apparence à d'autres formules que vous pouvez trouver ailleurs. 
Toutes ces formules sont généralement mathématiquement équivalentes et produisent les mêmes résultats. 
Elles sont plus ou moins faciles à utiliser selon les informations dont vous disposez...
Le lecteur intéressé par les mathématiques de la chose pourra trouver une justification complète de tout cela dans l'excellent manuel de Howell 
(en particulier le chapitre sur le test d'hypothèses appliqué aux moyennes).

A. Comparer la moyenne d'un échantillon et une constante de référence

Soit un échantillon de n mesures dont la moyenne est 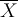\overline{X} et l'écart-type s.
On veut comparer la moyenne à une constante 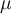\mu qui représente une certaine moyenne théorique.

  •   On calcule l'erreur-standard de l'échantillon, ES : 
    ES=\frac{s}{\sqrt{n}}
On a alors

t=\frac{\overline{X}-\mu}{ES}

où le nombre de degrés de liberté est ddl= n-1
 

Il faut encore calculer la taille de l'effet, qui pour les tests t est classiquement le d de Cohen. Ici,

d=\frac{\overline{X}-\mu}{s}

  • On détermine la valeur p d'avoir t(ddl)
  • On utilise la valeur de p pour prendre une décision statistique
  • On calcule la taille de l'effet
  • On présente les résultats inférentiels    

B. Comparer les moyennes de deux échantillons appariés

Soit un ensemble de n paires de mesures. On calcule une nouvelle variable constituant, pour chaque paire, la différence des deux mesures précédentes. Sous l'hypothèse nulle, la moyenne théorique de ces différences est zéro. La nouvelle variable constitue un échantillon unique dont la moyenne est 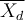\overline{X_d} et l'écart-type 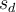s_d. On se ramène donc au cas d'une comparaison de moyenne (la moyenne des différences) et la constante \mu=0.

  • On calcule l'erreur-standard de l'échantillon des différences, ES_d : 
     
    ES_d=\frac{s_d}{\sqrt{n}}
    • On a alors

      t=\frac{\overline{X_d}-c}{ES_d}

      où le nombre de degrés de liberté est ddl= n-1

Il faut calculer la taille de l'effet, classiquement le d de Cohen. Ici, une formule simplifiée pour les groupes appariés le donne directement :

d=\frac{t}{\sqrt{n}}

  •   On détermine la valeur p d'avoir t(ddl)
  •   On utilise la valeur de p pour prendre une décision statistique
  •   On présente les résultats inférentiels.

C. Comparer les moyennes de deux échantillons indépendants


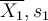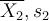Soient deux échantillons de mesures respectivement prises sur un groupe 1 de n1 sujets, et un groupe 2 de n2 sujets. Notons \overline{X_1}, s_1, et \overline{X_2}, s_2 les moyennes et écarts-types de ces deux échantillons.

La structure est la même pour tous les tests t : il s'agit de faire le rapport d'une différence de moyennes par une erreur standard. Dans le cas des mesures indépendantes, le calcul de l'erreur standard commune aux deux échantillons est compliqué par le fait que les effectifs des deux groupes peuvent différer (i.e., 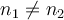n_1\neq n_2).

Les manuels distinguent souvent deux cas, selon que les effectifs sont équilibrés ou non, la relation se simplifiant dans le premier cas. Cela étant, la formule générale, quoique d'apparence un peu plus compliquée, marche dans tous les cas. À l'ère de l'informatique, nous ne voyons pas l'avantage d'enseigner deux formules aux étudiants de sciences humaines, au nom de la simplicité, quand la première suffit. Nous ne présentons donc ici que la formule générale.

On commence par calculer une sorte de variance combinée des deux groupes, souvent notée 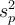s_p^2 dans les ouvrages ("p" pour "pooled" en anglais), et qui corrige notamment le problème des tailles inégales :

s_p^2=\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}

En prenant la racine de 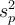s_p^2 on a un écart-type combiné, et on obtient alors t par la formule :

t=\frac{\overline{X_1}-\overline{X_2}}{\sqrt{s_p^2\bigg(\frac{1}{n_1}+\frac{1}{n_2}\bigg)}}

où le nombre de degrés de liberté : 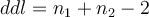ddl=n_1+n_2-2 .

Il faut encore calculer la taille de l'effet, qui pour les tests t est classiquement le d de Cohen. Ici, en nous appuyant sur le calcul de t déjà réalisé plus haut, nous disposons d'une formule qui marche même en cas d'échantillons d'effectifs différents :

d=\frac{t}{\frac{1}{n_1}+\frac{1}{n_2}}

  • On détermine la probabilité p d'avoir t(ddl)
  • On utilise la valeur de p pour prendre une décision statistique
  • On présente les résultats inférentiels.