La statistique d’écart studentisée
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L2 |
| Livre: | La statistique d’écart studentisée |
| Imprimé par: | Visiteur anonyme |
| Date: | mercredi 25 février 2026, 10:32 |
Description
Objectifs. Introduire une statistique qui est rarement utilisée pour elle-même, mais prend part à de nombreux tests post-hoc dans les ANOVA.
Prérequis. Test t de Student ; ANOVA
Résumé. La statistique d'écart studentisée q s'obtient en procédant à une sorte de test t portant sur les deux valeurs les plus extrêmes (haute et basse) d'un ensemble de moyennes. Une table des valeurs critiques de q en fonction du nombre de comparaisons impliquées dans l'ANOVA globale et le nombre de degrés de libertés de la comparaison est fournie.
1. Utilisation
La statistique d'écart studentisée ("studentized range" en anglais) notée q, est une fonction utilisée pour calculer différents tests post-hoc dans l'analyse de variance. Dans ce type de tests, plusieurs comparaisons de moyennes sont réalisées et l'on doit corriger le calcul de la valeur de significativité d'un test afin que l'erreur de l'ensemble des comparaisons ne dépasse pas le seuil qu'on se donne comme convention (généralement 5%, parfois 1% ou même moins, mais c'est rare pour les tests post-hoc).
La valeur q possède une distribution d’échantillonnage à partir de laquelle on peut construire des tables donnant ses valeurs critiques, c’est-à-dire les valeurs de q qu’il faut dépasser pour avoir une différence significative (voir par exemple la table de q que nous avons fournie en bas de cette page ou l'Annexe q de Howell). Les valeurs critiques de q, c'est-à-dire les valeurs que q doit dépasser pour être considéré comme significatif, dépendent de deux paramètres, le nombre r de groupes intervenant dans la comparaison globale (par exemple s’il y a 4 groupes, r =4), et le nombre de degrés de liberté de l'erreur de la comparaison globale (généralement N-k où N est le nombre total de sujets et k le nombre de groupes). C'est pourquoi on peut aussi la noter aussi qr,ddl en signalant ainsi directement les deux paramètres intéressants, la valeur de r et celle du nombre de degrés de libertés.
Pourquoi doit-on utiliser ce paramètre r ? Tout simplement parce que plus il y a de groupes, plus l’écart entre la moyenne la plus basse et la plus haute risque d’être élevée et donc si H0 globale est vraie, plus on risque de commettre une erreur de type I.
2. Calcul de q
On commence par ranger les moyennes des r différents groupes par ordre croissant de leurs valeurs moyennes, M1 , M2 ,..., Mr . La valeur q s’obtient très facilement à partir de la valeur t de comparaison des moyennes des deux groupes les plus extrêmes dans le classement, à savoir celui correspondant à M1 , la moyenne la plus faible et celui correspondant à Mr , la moyenne la plus forte. En effet, on a
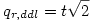
2.1. Cas avec variances homogènes
Vous pouvez aussi calculer q directement à partir de ces deux moyennes, M1 et Mr , sans passer par le calcul de t , en appliquant la formule :
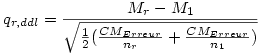
Le CMErreur s'obtient directement dans le tableau d'ANOVA. Bien sûr si les effectifs sont égaux, la formule précédente se simplifie puisqu'alors nr = n1.
2.2. Cas avec variances hétérogènes
Lorsque les échantillons sont de taille inégales mais les variances homogènes, Games et Howell (voir Howell, p. 384) ont proposé de calculer les choses séparément pour chaque paire de moyennes Mi , Mj :
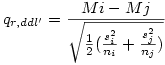
Le lecteur aura noté que la formule fait référence à ddl' et non plus simplement ddl. On compare donc q avec la valeur critique obtenue dans la table avec les paramètres r et le nombre de degrés de liberté ddl'. La valeur de ddl' à utiliser s'obtient par la formule
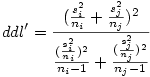
2. Une table des valeurs critiques de q au seuil de .05
Cette table a été réalisée par nos soins en utilisant la fonction "qtukey" du logiciel de statistiques R, et en faisant varier de 3 à 10 le nombre r de groupes impliqués dans la comparaison, et de 2 à 100 le nombre de degrés de libertés de la comparaison.
Ainsi par exemple pour une comparaison des deux moyennes les plus extrêmes parmi 6 ( r =6) groupes de 25 sujets chacun, la valeur que q devra dépasser pour que la comparaison soit significative est 4.358.
Nous n'avons pas indiqué les valeurs pour le cas r =2 car alors il n'y a pas véritablement lieu d'utiliser la statistique d'écart studentisée.
| ddl | r=3 | r=4 | r=5 | r=6 | r=7 | r=8 | r=9 | r=10 |
| 2 | 8.331 | 9.799 | 10.881 | 11.734 | 12.435 | 13.028 | 13.542 | 13.994 |
| 3 | 5.910 | 6.825 | 7.502 | 8.037 | 8.478 | 8.852 | 9.177 | 9.462 |
| 4 | 5.040 | 5.757 | 6.287 | 6.706 | 7.053 | 7.347 | 7.602 | 7.826 |
| 5 | 4.602 | 5.218 | 5.673 | 6.033 | 6.330 | 6.582 | 6.801 | 6.995 |
| 6 | 4.339 | 4.896 | 5.305 | 5.628 | 5.895 | 6.122 | 6.319 | 6.493 |
| 7 | 4.165 | 4.681 | 5.060 | 5.359 | 5.606 | 5.815 | 5.997 | 6.158 |
| 8 | 4.041 | 4.529 | 4.886 | 5.167 | 5.399 | 5.596 | 5.767 | 5.918 |
| 9 | 3.948 | 4.415 | 4.755 | 5.024 | 5.244 | 5.432 | 5.595 | 5.738 |
| 10 | 3.877 | 4.327 | 4.654 | 4.912 | 5.124 | 5.304 | 5.460 | 5.598 |
| 11 | 3.820 | 4.256 | 4.574 | 4.823 | 5.028 | 5.202 | 5.353 | 5.486 |
| 12 | 3.773 | 4.199 | 4.508 | 4.750 | 4.950 | 5.119 | 5.265 | 5.395 |
| 13 | 3.734 | 4.151 | 4.453 | 4.690 | 4.884 | 5.049 | 5.192 | 5.318 |
| 14 | 3.701 | 4.111 | 4.407 | 4.639 | 4.829 | 4.990 | 5.130 | 5.253 |
| 15 | 3.673 | 4.076 | 4.367 | 4.595 | 4.782 | 4.940 | 5.077 | 5.198 |
| 16 | 3.649 | 4.046 | 4.333 | 4.557 | 4.741 | 4.896 | 5.031 | 5.150 |
| 17 | 3.628 | 4.020 | 4.303 | 4.524 | 4.705 | 4.858 | 4.991 | 5.108 |
| 18 | 3.609 | 3.997 | 4.276 | 4.494 | 4.673 | 4.824 | 4.955 | 5.071 |
| 19 | 3.593 | 3.977 | 4.253 | 4.468 | 4.645 | 4.794 | 4.924 | 5.037 |
| 20 | 3.578 | 3.958 | 4.232 | 4.445 | 4.620 | 4.768 | 4.895 | 5.008 |
| 21 | 3.565 | 3.942 | 4.213 | 4.424 | 4.597 | 4.743 | 4.870 | 4.981 |
| 22 | 3.553 | 3.927 | 4.196 | 4.405 | 4.577 | 4.722 | 4.847 | 4.957 |
| 23 | 3.542 | 3.914 | 4.180 | 4.388 | 4.558 | 4.702 | 4.826 | 4.935 |
| 24 | 3.532 | 3.901 | 4.166 | 4.373 | 4.541 | 4.684 | 4.807 | 4.915 |
| 25 | 3.523 | 3.890 | 4.153 | 4.358 | 4.526 | 4.667 | 4.789 | 4.897 |
| 26 | 3.514 | 3.880 | 4.141 | 4.345 | 4.511 | 4.652 | 4.773 | 4.880 |
| 27 | 3.506 | 3.870 | 4.130 | 4.333 | 4.498 | 4.638 | 4.758 | 4.864 |
| 28 | 3.499 | 3.861 | 4.120 | 4.322 | 4.486 | 4.625 | 4.745 | 4.850 |
| 29 | 3.493 | 3.853 | 4.111 | 4.311 | 4.475 | 4.613 | 4.732 | 4.837 |
| 30 | 3.486 | 3.845 | 4.102 | 4.301 | 4.464 | 4.601 | 4.720 | 4.824 |
| 31 | 3.481 | 3.838 | 4.094 | 4.292 | 4.454 | 4.591 | 4.709 | 4.812 |
| 32 | 3.475 | 3.832 | 4.086 | 4.284 | 4.445 | 4.581 | 4.698 | 4.802 |
| 33 | 3.470 | 3.825 | 4.079 | 4.276 | 4.436 | 4.572 | 4.689 | 4.791 |
| 34 | 3.465 | 3.820 | 4.072 | 4.268 | 4.428 | 4.563 | 4.680 | 4.782 |
| 35 | 3.461 | 3.814 | 4.066 | 4.261 | 4.421 | 4.555 | 4.671 | 4.773 |
| 36 | 3.457 | 3.809 | 4.060 | 4.255 | 4.414 | 4.547 | 4.663 | 4.764 |
| 37 | 3.453 | 3.804 | 4.054 | 4.249 | 4.407 | 4.540 | 4.655 | 4.756 |
| 38 | 3.449 | 3.799 | 4.049 | 4.243 | 4.400 | 4.533 | 4.648 | 4.749 |
| 39 | 3.445 | 3.795 | 4.044 | 4.237 | 4.394 | 4.527 | 4.641 | 4.741 |
| 40 | 3.442 | 3.791 | 4.039 | 4.232 | 4.388 | 4.521 | 4.634 | 4.735 |
| 41 | 3.439 | 3.787 | 4.035 | 4.227 | 4.383 | 4.515 | 4.628 | 4.728 |
| 42 | 3.436 | 3.783 | 4.030 | 4.222 | 4.378 | 4.509 | 4.622 | 4.722 |
| 43 | 3.433 | 3.779 | 4.026 | 4.217 | 4.373 | 4.504 | 4.617 | 4.716 |
| 44 | 3.430 | 3.776 | 4.022 | 4.213 | 4.368 | 4.499 | 4.611 | 4.710 |
| 45 | 3.428 | 3.773 | 4.018 | 4.209 | 4.364 | 4.494 | 4.606 | 4.705 |
| 46 | 3.425 | 3.770 | 4.015 | 4.205 | 4.359 | 4.489 | 4.601 | 4.700 |
| 47 | 3.423 | 3.767 | 4.011 | 4.201 | 4.355 | 4.485 | 4.597 | 4.695 |
| 48 | 3.420 | 3.764 | 4.008 | 4.197 | 4.351 | 4.481 | 4.592 | 4.690 |
| 49 | 3.418 | 3.761 | 4.005 | 4.194 | 4.347 | 4.477 | 4.588 | 4.686 |
| 50 | 3.416 | 3.758 | 4.002 | 4.190 | 4.344 | 4.473 | 4.584 | 4.681 |
| 51 | 3.414 | 3.756 | 3.999 | 4.187 | 4.340 | 4.469 | 4.580 | 4.677 |
| 52 | 3.412 | 3.753 | 3.996 | 4.184 | 4.337 | 4.465 | 4.576 | 4.673 |
| 53 | 3.410 | 3.751 | 3.994 | 4.181 | 4.334 | 4.462 | 4.572 | 4.669 |
| 54 | 3.408 | 3.749 | 3.991 | 4.178 | 4.331 | 4.459 | 4.569 | 4.666 |
| 55 | 3.406 | 3.747 | 3.989 | 4.176 | 4.328 | 4.455 | 4.566 | 4.662 |
| 56 | 3.405 | 3.745 | 3.986 | 4.173 | 4.325 | 4.452 | 4.562 | 4.659 |
| 57 | 3.403 | 3.743 | 3.984 | 4.170 | 4.322 | 4.449 | 4.559 | 4.656 |
| 58 | 3.402 | 3.741 | 3.982 | 4.168 | 4.319 | 4.447 | 4.556 | 4.652 |
| 59 | 3.400 | 3.739 | 3.979 | 4.165 | 4.317 | 4.444 | 4.553 | 4.649 |
| 60 | 3.399 | 3.737 | 3.977 | 4.163 | 4.314 | 4.441 | 4.550 | 4.646 |
| 61 | 3.397 | 3.735 | 3.975 | 4.161 | 4.312 | 4.438 | 4.548 | 4.643 |
| 62 | 3.396 | 3.734 | 3.973 | 4.159 | 4.309 | 4.436 | 4.545 | 4.641 |
| 63 | 3.395 | 3.732 | 3.972 | 4.157 | 4.307 | 4.434 | 4.542 | 4.638 |
| 64 | 3.393 | 3.730 | 3.970 | 4.155 | 4.305 | 4.431 | 4.540 | 4.635 |
| 65 | 3.392 | 3.729 | 3.968 | 4.153 | 4.303 | 4.429 | 4.538 | 4.633 |
| 66 | 3.391 | 3.727 | 3.966 | 4.151 | 4.301 | 4.427 | 4.535 | 4.630 |
| 67 | 3.390 | 3.726 | 3.965 | 4.149 | 4.299 | 4.425 | 4.533 | 4.628 |
| 68 | 3.389 | 3.725 | 3.963 | 4.147 | 4.297 | 4.423 | 4.531 | 4.626 |
| 69 | 3.387 | 3.723 | 3.962 | 4.146 | 4.295 | 4.421 | 4.529 | 4.624 |
| 70 | 3.386 | 3.722 | 3.960 | 4.144 | 4.293 | 4.419 | 4.527 | 4.621 |
| 71 | 3.385 | 3.721 | 3.959 | 4.142 | 4.291 | 4.417 | 4.525 | 4.619 |
| 72 | 3.384 | 3.719 | 3.957 | 4.141 | 4.290 | 4.415 | 4.523 | 4.617 |
| 73 | 3.383 | 3.718 | 3.956 | 4.139 | 4.288 | 4.413 | 4.521 | 4.615 |
| 74 | 3.382 | 3.717 | 3.954 | 4.138 | 4.286 | 4.411 | 4.519 | 4.613 |
| 75 | 3.382 | 3.716 | 3.953 | 4.136 | 4.285 | 4.410 | 4.517 | 4.611 |
| 76 | 3.381 | 3.715 | 3.952 | 4.135 | 4.283 | 4.408 | 4.515 | 4.610 |
| 77 | 3.380 | 3.714 | 3.951 | 4.133 | 4.282 | 4.406 | 4.514 | 4.608 |
| 78 | 3.379 | 3.713 | 3.949 | 4.132 | 4.280 | 4.405 | 4.512 | 4.606 |
| 79 | 3.378 | 3.712 | 3.948 | 4.131 | 4.279 | 4.403 | 4.510 | 4.604 |
| 80 | 3.377 | 3.711 | 3.947 | 4.129 | 4.277 | 4.402 | 4.509 | 4.603 |
| 81 | 3.377 | 3.710 | 3.946 | 4.128 | 4.276 | 4.400 | 4.507 | 4.601 |
| 82 | 3.376 | 3.709 | 3.945 | 4.127 | 4.275 | 4.399 | 4.506 | 4.600 |
| 83 | 3.375 | 3.708 | 3.944 | 4.126 | 4.274 | 4.398 | 4.504 | 4.598 |
| 84 | 3.374 | 3.707 | 3.943 | 4.125 | 4.272 | 4.396 | 4.503 | 4.597 |
| 85 | 3.374 | 3.706 | 3.942 | 4.123 | 4.271 | 4.395 | 4.502 | 4.595 |
| 86 | 3.373 | 3.705 | 3.941 | 4.122 | 4.270 | 4.394 | 4.500 | 4.594 |
| 87 | 3.372 | 3.704 | 3.940 | 4.121 | 4.269 | 4.392 | 4.499 | 4.592 |
| 88 | 3.371 | 3.704 | 3.939 | 4.120 | 4.268 | 4.391 | 4.498 | 4.591 |
| 89 | 3.371 | 3.703 | 3.938 | 4.119 | 4.266 | 4.390 | 4.496 | 4.590 |
| 90 | 3.370 | 3.702 | 3.937 | 4.118 | 4.265 | 4.389 | 4.495 | 4.588 |
| 91 | 3.370 | 3.701 | 3.936 | 4.117 | 4.264 | 4.388 | 4.494 | 4.587 |
| 92 | 3.369 | 3.700 | 3.935 | 4.116 | 4.263 | 4.387 | 4.493 | 4.586 |
| 93 | 3.368 | 3.700 | 3.934 | 4.115 | 4.262 | 4.386 | 4.492 | 4.585 |
| 94 | 3.368 | 3.699 | 3.934 | 4.114 | 4.261 | 4.384 | 4.490 | 4.583 |
| 95 | 3.367 | 3.698 | 3.933 | 4.114 | 4.260 | 4.383 | 4.489 | 4.582 |
| 96 | 3.367 | 3.698 | 3.932 | 4.113 | 4.259 | 4.382 | 4.488 | 4.581 |
| 97 | 3.366 | 3.697 | 3.931 | 4.112 | 4.258 | 4.381 | 4.487 | 4.580 |
| 98 | 3.366 | 3.696 | 3.930 | 4.111 | 4.257 | 4.380 | 4.486 | 4.579 |
| 99 | 3.365 | 3.696 | 3.930 | 4.110 | 4.257 | 4.379 | 4.485 | 4.578 |
| 100 | 3.365 | 3.695 | 3.929 | 4.109 | 4.256 | 4.379 | 4.484 | 4.577 |
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte