Statistique : comparer des moyennes
2. Comparer deux moyennes : test du t de Student
2.3. Comparer deux échantillons indépendants.
Puisque l'on a deux groupes de sujets, on a aussi deux moyennes m1 et m2 . L'hypothèse nulle revient à poser que m1 = m2. Un test significatif indiquera que les données ne sont pas très compatibles avec l'hypothèse nulle et donc qu'on a plus probablement m1 ≠ m2.

Préalables spécifiques de cette version du test de Student :
- 1. Il faut soit avoir deux échantillons de données recueillies sur deux groupes de sujets différents.
- 2. Les données devraient idéalement être normalement distribuées.Cliquez ici pour voir comment tester la normalité de la distribution.
- 3. Les variances des échantillons réels devraient idéalement être homogènes. Sous SPSS ou Statistica par exemple, le "test de Levene" ne doit pas être significatif. Toutefois cette condition n'est pas rédhibitoire car les logiciels donnent alors des valeurs de p corrigées, selon des méthodes que nous ne détaillerons pas ici. Il suffit de vérifier l'homogénéité. Sous SPSS par exemple, si le test de Levene est significatif, on prendra alors la valeur de p calculée pour les variances non homogènes.
A. Calculer la valeur de
t
A.1. Pour les pressés : "En bref"
Liens de pratique avec un logiciel de statistiques : Voir ici des vidéos et textes pratiques
Soient deux échantillons réels, respectivement d'effectifs, moyennes et écarts-types
n1
,
m1,
s1
, et
n2
,
m2
,
s2
.
On commence par calculer l'erreur standard ESv de l'échantillon virtuel constitué par les deux échantillons indépendants :
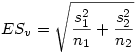
Et ensuite le t est donné par la formule
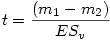
On présente le résultat en écrivant t(ddl)=n.nn (pour la présentation de la valeur p , voir l'article général sur la norme APA de présentation d'une valeur p).
A.2. Pour ceux qui aiment comprendre : D'où cela vient-il ?
Dans le test du t de Student, la statistique calculée est précisément la valeur t. Dans le cas de la comparaison de deux échantillons indépendants, voyons quelle formule employer. Commençons par rappeler la formule générale du t :
Soient mv la moyenne d'un échantillon virtuel de taille nv et ESv son erreur-standard, on a
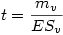
Ici notre échantillon virtuel est composé des deux échantillons indépendants réels. Sa moyenne est mv = (m1 - m2) où m1 et m2 sont les moyennes des deux échantillons réels.
Le calcul de ESv l'erreur standard de l'échantillon virtuel est moins naturel. En effet, ces deux échantillons étant indépendants, ils renvoient à des effectifs de taille potentiellement différentes et l'erreur standard de deux échantillons de tailles différentes ne s'obtient malheureusement pas en faisant simplement la moyenne des erreurs-standards. L'écart-type de l'échantillon virtuel issu de deux échantillons de tailles n1 et n2, de moyennes m1 et m2, et d'écarts-types s1 et s2 peut s'obtenir de la façon suivante :
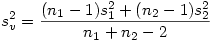
On produit alors l'ES standard de l'échantillon virtuel par la formule
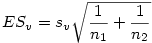
Finalement, il ne reste plus qu'à calculer
t
:
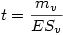
B. Comment obtenir la valeur p associée ?
Il nous faut connaître la valeur t et le ddl nombre de degrés de libertés.
Si elle n'est pas directement donnée par votre logiciel de statistique, la valeur p associée s'obtient
- soit en regardant dans une table du t de Student en prenant comme entrée la valeur du t ainsi calculée et comme nombre de degrés de libertés la valeur n-1 où n est le nombre de mesures.
- Soit au moyen d'une formule de tableur sous Microsoft Office Excel ou OpenOffice Calc : "=LOI.STUDENT.BILATERALE( t ; ddl )"
Par défaut, on travaillera en bilatéral et on se contentera de la valeur
p
précédemment obtenue.
Si toutefois on dispose d'une hypothèse orientée et que les statistiques descriptives vont dans le sens attendu (typiquement, on s'attend à ce que m1 > m2 et c'est le cas au niveau descriptif, ou bien on s'attend à ce que m1 < m2 et c'est le cas au niveau descriptif), alors on peut travailler en unilatéral : il suffit alors de prendre la valeur p précédemment obtenue et de la diviser par 2 avant de décider si le test est significatif ou non.
C. Un exemple
Supposons que l'on ait une hypothèse théorique (fictive) selon laquelle les premiers astronautes envoyés devraient avoir plus de 38 ans en moyenne, mais que ceux envoyés après une certaine date sont plus jeunes. Imaginons que la seule information dont nous disposions est l'âge des astronautes au moment de leur sortie sur notre satellite, et supposons encore que 6 de ces astronautes appartiennent au premier groupe, et les 6 autres au deuxième groupe. Nous obtenons le tableau suivant :
| Individu | Groupe |
Age
|
| 1 |
1
|
32 |
| 2 | 1 | 38 |
| 3 | 1 | 36 |
| 4 | 1 | 37 |
| 5 | 1 | 42 |
| 6 | 1 | 26 |
| 7 | 2 | 39 |
| 8 | 2 | 35 |
| 9 | 2 | 33 |
| 10 | 2 | 34 |
| 11 | 2 | 37 |
| 12 | 2 | 36 |
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des âges pour chacun des deux groupes, soit
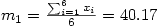
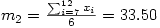
et
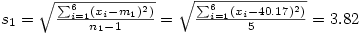
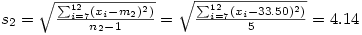
Attention au fait que dans ce cas, le tableau représente un échantillon de la population totale des astronautes et l'on utilise la formule de l'écart-type pour échantillon (on divise par n -1) et non de l'écart-type pour population (où l'on divise par n).
L'écart-type de l'échantillon virtuel issu de deux échantillons de tailles n1 et n2, de moyennes m1 et m2, et d'écarts-types s1 et s2 peut s'obtenir de la façon suivante :
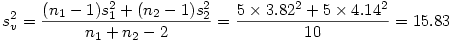
Il ne reste alors qu'à produire l'ES de l'échantillon virtuel par la formule
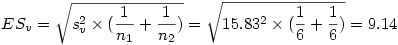
Finalement, il ne reste plus qu'à calculer
t
:
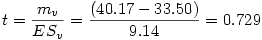
Ensuite sous Excel par exemple, en appliquant la formule =LOI.STUDENT.BILATERALE(t ; ddl)" avec le t que l'on vient de calculer et ddl=6+6-2=10 degrés de libertés, on trouve p =0.48255927.
Pour un test du t , la question suivante à se poser concernerait le caractère bilatéral ou non du test. Ici, de toute façon, même si on divisait par deux la valeur de p, on serait encore très largement au dessus du seuil de signification, donc ce n'est pas la peine d'aller plus loin : le test n'est pas significatif et l'on ne peut pas conclure qu'il existe une différence entre les groupes.
On pourra rapporter le résultat en disant que "t(10)=0.73, ns" (norme APA 6e édition), ou mieux en rapportant la valeur p arrondie à deux ou trois décimales (norme APA 7e édition).
- 1. Il faut soit avoir deux échantillons de données recueillies sur deux groupes de sujets différents.
- 2. Les données devraient idéalement être normalement distribuées. Cliquez ici pour voir comment tester la normalité de la distribution.
- 3. Les variances des échantillons réels devraient idéalement être homogènes. Sous SPSS ou Statistica par exemple, le "test de Levene" ne doit pas être significatif. Il est alors souhaitable d'utiliser la variante dite "test de Welch", qui est disponible dans jamovi et est même le test de Student par défaut dans R.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte