UOH / Statistique et Psychométrie en L2
Résumé de section
-
-
Ce module de niveau L2 de psychologie est organisé en quatre parties :- "Comprendre" : Un cours théorique composé de quatre "grandes leçons"
- "Savoir-Faire" : Un ensemble de ressources pratiques, de tutoriels (dont des vidéos)
- "Zoom sur" : Un complément d'approfondissement du cours théorique, formé de leçons spécialisées
- "Rappels de maths" : Pour les étudiants intéressés à certains détails techniques ou qui veulent se rafraîchir la mémoire
-
-
La partie "Comprendre" est organisée autour de quatre « Grandes Leçons », chacune composée d'une série d'articles d'une ou plusieurs pages, et se concluant par un QCM d'auto-évaluation.
-
Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette leçon est essentielle pour comprendre les suivantes, car tous les concepts de base de la statistique inférentielle y sont expliqués.
-
Le titre développé de cette grande leçon est « Du qualitatif au quantitatif : théorie et applications ». Consacrée à la psychométrie, elle approfondit la problématique de la mesure en psychologie selon deux perspectives. - D’une part, il s’agit d’expliciter la construction d’un observable comme le processus de composition d’applications, processus qui permet de transcrire des énoncés qualitatifs en énoncés quantitatifs.
- D’autre part, il s’agit de montrer comment l’utilisation des prévisions qu’il est possible de dériver statistiquement à partir des « sorties » de l’observation psychotechnique étaye l’intervention du psychologue dans des problématiques de dépistage, de sélection et de conseil.
-
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
-
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
-
-
Cette rubrique présente une série d'articles où sont exposées les procédures permettant de calculer les statistiques présentées dans les autres articles.
Ces calculs utilisent différents logiciels. Nous nous sommes efforcés de faire appel à des logiciels libres de droit, comme Open Office, jamovi, ou R, ce qui permet d'éviter de défavoriser les étudiants peu fortunés. Quelques procédures peuvent cependant être présentées au moyen de logiciels payants (SPSS, Statistica, Excel).
Le logiciel à la fois le plus puissant et gratuit, le logiciel R, est malheureusement un peu complexe d'utilisation, car il requiert des compétences en programmation). Jamovi fournit cependant une interface gratuite et intuitive qui s'enrichit constamment de nouvelles procédures. Sans doute le choix le plus judicieux actuellement pour un étudiant de L2, jamovi fournit en outre une interface vers R qui peut permettre à ceux qui se destinent à la recherche d'entrer en douceur dans le monde de R, ou encore de produire des graphiques plus personnalisés.
-
Objectifs : Cette section comporte un ensemble de tutoriels visant à montrer comment réaliser concrètement des tests de comparaison de moyennes à deux groupes (t de student et Welch) ou plus (ANOVA) avec des logiciels...
Prérequis. Cours de L1 : Statistiques descriptives et cours de L2 : les comparaisons de moyennes
Résumé.
- test t à groupes indépendants (avec variante Welch)
- test t à échantillon unique
- test t à groupes appariés
- ANOVA à un facteur
Logiciels considérés : Jamovi, R
- test t à groupes indépendants (avec variante Welch)
-
Objectifs. Cette section comporte un ensemble de vidéos montrant comment comparer deux groupes lorsqu'un test paramétrique n'est pas utilisable, par exemple lorsque la distribution normale n'est pas respectée ou que la variable dépendante est seulement ordinale.
Prérequis.
- Cours de L1 : Statistiques descriptives
- Grandes leçons sur les statistiques inférentielles et sur les comparaisons de groupes
-
C'est une chose de réaliser un test avec un logiciel, c'est-à-dire lui fournir des données et lui faire produire les valeurs t et p, c'est en une autre de savoir interpréter les sorties du logiciel.
Cette section présente les interprétations de sorties de différents logiciels pour...- test t à échantillon unique
- test t à groupes appariés
- test t à groupes indépendants
Logiciels considérés : Jamovi, R, SPSS, Statistica, Tableurs
-
Lorsque l'on réalise des tests statistiques "à la main", c'est-à-dire en appliquant soi-même des formules, par opposition à l'utilisation d'un logiciel de statistiques qui contient des formules pré-programmées, on calcule une certaine statistique (par exemple le t de student ou le), qu'il faut ensuite convertir en valeur p pour prendre une décision.
Dans la plupart des cas, il n'y a pas de formule simple pour calculer ces valeurs p et l'on va donc utiliser des tables permettant la conversion entre certaines valeurs que peut prendre la statistique t calculée et les valeurs p. requises pour la décision statistique. On recourt alors à des tables dont on explique ici l'utilisation. -
Objectifs : Expliquer à l'étudiant en psychologie comment il doit présenter ses résultats concernant les valeurs p. Lui apprendre à savoir interpréter les résultats qu'il pourra lire dans les articles scientifiques.
Pré-requis:
- Notion de probabilité, article La statistique inférentielle comme décision
Résumé : L'article répond à des questions de base sur le nombre de décimales à utiliser, quand utiliser un point ou une virgule décimale, faut-il mettre un zéro avant le point décimal, comment rapporter une valeur p très faible, ou au contraire non significative, etc...
-
Cette section présente un ensemble de formules permettant de réaliser manuellement des tests t de student.
- test t à échantillon unique
- test t à groupes appariés
- test t à groupes indépendants
Pour chacun des types de test, une formule donne la taille d'effet sous forme du d de Cohen.
-
-
La rubrique "Zoom sur..." présente un certain nombre de points d'entrée vers des rubriques concepts « essentiels » qui font chacun l'objet d'un article spécifique, en complément des grandes leçons présentées dans la rubrique "Comprendre" :
-
Objectifs. Définir et illustrer la notion d'algèbre d'événements.
Prérequis.
Résumé. La notion de fréquence conditionnelle repose sur la donnée d'un couple de variables discrètes (X, Y). La fréquence d'une certaine valeur yj en Y conditionnellement à une certaine valeur xi en X est la proportion des cas de la classe xi qui ont pour valeur yj.
-
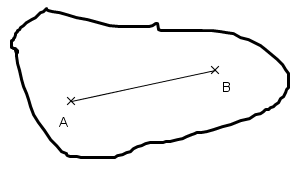
Objectifs. Montrer que l'espérance d'une variable aléatoire numérique discrète bornée est comprise entre les bornes inférieure et supérieure de la variable.
Prérequis.
Résumé. On procède en deux temps : 1) montrer que l'espérance est supérieure ou égale à la valeur minimale de la variable, 2), montrer que l'espérance est inférieure ou égale à la valeur maximale de la variable.
-
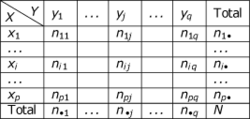
Objectifs. Définir la notion de fréquence conditionnelle.
Prérequis.
Résumé. La notion de fréquence conditionnelle repose sur la donnée d'un couple de variables discrètes (X, Y). La fréquence d'une certaine valeur yj en Y conditionnellement à une certaine valeur xi en X est la proportion des cas de la classe xi qui ont pour valeur yj .
-
Prérequis. Produit cartésien.
Résumé. Pour qu'un vecteur domine un autre vecteur, chacune de ses composantes doit dominer chacune des composantes respectives de l'autre vecteur.
-
Objectifs. Introduire une statistique qui est rarement utilisée pour elle-même, mais prend part à de nombreux tests post-hoc dans les ANOVA.
Prérequis. Test t de Student ; ANOVA
Résumé. La statistique d'écart studentisée q s'obtient en procédant à une sorte de test t portant sur les deux valeurs les plus extrêmes (haute et basse) d'un ensemble de moyennes. Une table des valeurs critiques de q en fonction du nombre de comparaisons impliquées dans l'ANOVA globale et le nombre de degrés de libertés de la comparaison est fournie.
-
Objectifs. Expérimenter par soi-même le devenir de la fréquence d'occurrence d'un événement lorsque cet événement résulte d'un processus probabiliste (expérience aléatoire qui se répète).
Prérequis. Aucun
Résumé. La fréquence d'occurrence d'un événement de probabilité p converge vers p lorsque le nombre d'expériences augmente.
-
-
La rubrique « Rappels de maths » est une aide destinée à rappeler certaines notions mathématiques de base qui ont pu être oubliées.
L'étudiant trouvera ici une approche de ces concepts sur plusieurs niveaux. Les articles listés plus bas constituent les points d'entrée principaux, mais des démonstrations sont aussi disponibles depuis l'intérieur des articles pour ceux qui souhaitent consolider leur maîtrise des outils mathématiques de base.
-
Lectures conseillées
Danziger, K. (1990). Constructing the subject. Historical origins of psychological research . New York: Cambridge University Press.
Granger, G.-G. (1995). La science et les sciences (2e éd. corrigée). Paris : Presses Universitaires de France.
Noël, Y. (2013). Psychologie statistique avec R, coll. Pratique R, Paris: Springer. http://www.springer.com/psychology/book/978-2-8178-0424-8
Popper, K. R. (1973). La logique de la découverte scientifique. Paris : Payot.
Références utilisées et/ou citées dans le site
- Atlan, H. (2010). De la fraude. Le monde de l'onaa. Paris : Seuil.
- Barbut, M., & Monjardet, B. (1970). Ordre et classification, algèbre et combinatoire, tome 1. Paris : Hachette.
- Canguilhem, G. (1958). Qu'est-ce que la psychologie ? Revue de Métaphysique et de Morale, 1, 12-25.
- Cronbach, L. J. (1990). Essentials of psychological testing (5th ed.). New York: HarperCollins.
- Desrosières, A. (2000). La politique des grands nombres. Histoire de la raison statistique. Paris : La Découverte.
- Howell, D.C. (1998). Méthodes Statistiques en Sciences Humaines. Paris, De Boeck.
- Lamiell, J.T. (2003). Beyond individual and group differences. Human individuality, scientific psychology, and William Stern's critical personalism. Thousand Oaks: Sage.
- Rényi, A. (1966). Calcul des probabilités. Paris : Dunod.
- Rioux, L., & Mokounkolo, R. (2004). Attachement au quartier et adolescence. Étude comparative dans deux banlieues à forte diversité culturelle. Bulletin de Psychologie, 57, 611-620.
- Searle, J. R. (1995). The construction of social reality. New York. The Free Press.
-
Steiger, J.H. (1980). Tests for comparing elements of a correlation matrix. Psychological Bulletin, 87 , 2, 245-251.
- Vautier, S., Veldhuis, M., Lacot, E., & Matton, N. (2012). The ambiguous utility of psychometrics for the interpretative founding of socially relevant avatars. Theory & Psychology, 22 , 810-822.
Couleur de fond
Font Face
Taille de police
Couleur de texte
