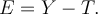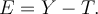Variables de scores vrais et d'erreurs
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L1 |
| Livre: | Variables de scores vrais et d'erreurs |
| Imprimé par: | Visiteur anonyme |
| Date: | jeudi 9 mai 2024, 03:36 |
Description
Objectifs.
Définir les concepts de variables de scores vrais et d'erreurs.
Prérequis.
Résumé.
Une variable de scores vrais, notée
T, est définie par rapport à une variable
Y
de scores psychométriques. Alors que la variable
Y
est définie de telle sorte que la même personne puisse obtenir des scores variables, la variable
T
assigne à chaque personne un score unique, son score vrai, c'est-à-dire l'espérance mathématique des scores qu'elle peut obtenir. La variable d'erreurs
E
est définie par la différence
Les variables
T
et
E
n'ont pas de valeur observable. Ce sont des variables latentes. rédaction initiale : Stéphane Vautier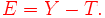
1. Variable de scores vrais
Prenons comme point de départ une variable aléatoire Y définie comme application d'un ensemble Ω = U × A dans l'ensemble des scores associés aux observations possibles dans A. Pour chaque personne de U, on considère le score vrai (i.e., l'espérance mathématique) des scores possibles pour cette personne. De cette manière, le score vrai de chaque personne est un nombre unique, appartenant à l'ensemble des nombres réels. De la même manière, par exemple, l'âge de la personne est un score unique associée à cette personne au moment où l'on réalise l'expérience aléatoire (voir l'article Variable aléatoire, § 1), parce que l'âge n'a pas de variabilité intrinsèque lorsqu'on s'intéresse à une personne.
Ainsi, on considère l'expérience aléatoire qui consiste à tirer au sort une personne dans U et à s'intéresser non pas à un score possible parmi un ensemble de ses scores observables, mais à l'unique score latent qui résume au mieux la variabilité de ses scores observables. Comme la personne qui est tirée au sort peut varier, le score vrai qui est associé à cette personne peut varier également.
Soit un test particulier appliqué à une population P de personnes en une occasion de test donnée. On considère pour chaque personne l'ensemble des scores qu'elle aurait s'il était possible de répéter le test indéfiniment et sans apprentissage. Appelons S l'ensemble de ces ensembles. On considère l'espérance mathématique de chaque ensemble de S. Les nombres ainsi définis forment un ensemble T. Ainsi, la variable des scores vrais est définie par la composition de l'application de P dans S et de S dans T, qui a toute personne de P attribue un unique score vrai associé à l'expérience du test.
2. Variable d'erreurs
On peut effectuer des additions, des soustractions et des multiplications de variables aléatoires quantitatives. Considérons plus particulièrement la variable Y des scores psychométriques et la variable T des scores vrais, Y et T étant définies pour une même population de personnes et une certaine application d'un test donné.
On définit la variable d'erreurs E comme la différence
3. Propriétés importantes
On démontre (e.g., Steyer, 1989) que :
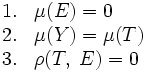
La première proposition stipule que la moyenne de la variable des erreurs est nulle. La seconde proposition se déduit de la première : la moyenne de la variable des scores observés est égale à la moyenne des scores vrais. La troisième proposition énonce que la corrélation entre les erreurs et les scores vrais est nulle.