Relation d'équivalence
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L1 |
| Livre: | Relation d'équivalence |
| Imprimé par: | Visiteur anonyme |
| Date: | jeudi 9 mai 2024, 17:44 |
Description
Objectifs :
définir le concept de relation d'équivalence, fondamental pour la classification des éléments d'un ensemble ; définir les concepts associés de partition et d'ensemble quotient.
Prérequis :
aucun.
Utilisé comme prérequis dans les articles : Échelles de mesure
Résumé :
une relation d'équivalence rédaction : Stéphane Vautier
est une relation binaire définie sur un ensemble E. est réflexive, symétrique et transitive. définit une partition de E. L'ensemble quotient E/ est l'ensemble des parties de E induites par .
1. Définitions
Les éléments de définition qui suivent sont empruntés à Barbut et Monjardet (1970a). On considère un ensemble E composé d'au moins deux éléments distincts. On considère une relation binaire R permettant de mettre les éléments de E en relation.
La relation est une relation d'équivalence si elle possède les trois propriétés suivantes :
- pour tout x de E,
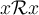: réflexivité ; - pour tout x, y de E,
: symétrie ; - pour tout x, y, z de E,
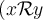et 
: transitivité.
La classe d'équivalence d'un élément x de E est la partie de E formée de tous les éléments qui sont en relation avec x. Les parties de E obtenues comme classe d'équivalence d'un élément x de E sont les classes d'équivalence induites par . Ces classes d'équivalence forment une partition de E. L'ensemble quotient, noté E/R, est l'ensemble des classes d'équivalences induites par .
2. Exemple : les modalités de la variable Sexe
Le premier paragraphe de l'article Relations entre statistique et psychométrie présente la notion d'échelle nominale à partir de l'exemple de la catégorisation des humains selon leur sexe. Cette catégorisation est un exemple de relation d'équivalence définie sur l'ensemble des êtres humains. Nous allons voir dans ce paragraphe comment la notion mathématique de relation d'équivalence interprète de manière formelle ces catégories.
On s'intéresse au concept de sexuation chez les jeunes enfants. On demande à un enfant, par exemple le petit frère du meilleur copain de Kid Paddle, de classer les personnes de l'ensemble H = {Paul, Jacques, Marie, Brigitte, ...}, en procédant par comparaison avec un modèle :
"Tu vois ce personnage ? Il s'appelle Paul. Et ce personnage, là, il s'appelle Jacques. Jacques est comme Paul parce que c'est un garçon et que Paul aussi est un garçon. Et tu vois cet autre personnage ? Elle s'appelle Lucie. Lucie n'est pas comme Paul parce que c'est une fille. Brigitte est comme Lucie parce que Brigitte est une fille, comme Lucie."
Après avoir comparé les personnages de l'ensemble H avec le modèle "Paul", l'enfant aboutit à deux groupes :
- les garçons,
- les filles.
On choisit à présent un autre "modèle", par exemple, Jacques, et on demande au petit frère du copain de Kid Paddle de comparer toutes les personnes de l'ensemble H à Jacques dans les mêmes termes, si bien que le petit frère parvient aux deux groupes auxquels il est parvenu avec le modèle"Paul".
Supposons à présent que l'enfant parvienne aux mêmes groupes avec le modèle "Brigitte", et que finalement il parvienne toujours aux deux mêmes groupes de personnes, quel que soit le modèle utilisé pour classer ces personnes.
Alors le petit frère du copain de Kid Paddle a établi une relation d'équivalence, que l'on pourra par exemple interpréter comme une bonne preuve de sa connaissance du concept de sexuation.
Dans la pratique en psychologie, lorsqu'on appréhende les catégories d'une classification, on appréhende les éléments de l'ensemble quotient de la relation d'équivalence : fille vs. garçon. Selon cette perspective, on utilise la relation "appartenir à", qui est formellement fondée sur la relation "avoir la même propriété que".
3. Relation d'équivalence et objectivité
Toute relation d'équivalence est associée à une catégorisation. Ces catégories sont-elles objectives ? Ce problème des catégories objectives présente un aspect épistémologique : considérant deux éléments x et y quelconques de E, comment décider que "
" est vrai ?
Si on considère l'exemple de la relation d'équivalence fondée sur le caractère masculin vs. féminin des êtres humains, comment décide-t-on que telle personne est du même caractère que telle autre ? Tout d'abord, on peut en principe vérifier que la relation d'équivalence existe pour une personne donnée en lui demandant d'établir des groupes selon la procédure détaillée dans le paragraphe précédent. Si on constate que les groupes produits par cette personne varient d'un modèle à l'autre, la notion de catégorisation est indéfinie pour cette personne, puisqu'on ne peut pas l'associer à une relation d'équivalence.
Bien souvent, les critères de catégorisation ne sont pas explicites, mais nous sommes capables de produire des jugements de classification conformes à la structure d'une relation d'équivalence. Il suffit qu'en principe le résultat des jugements de classification ne dépende pas de la personne qui effectue le jugement pour qu'on puisse considérer qu'une catégorisation, , soit vraie ou fausse.