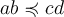Psychométrie : théorie et applications
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L2 |
| Livre: | Psychométrie : théorie et applications |
| Imprimé par: | Visiteur anonyme |
| Date: | jeudi 12 février 2026, 20:51 |
Description
 Le titre développé de cette grande leçon est « Du qualitatif au quantitatif : théorie et applications ». Consacrée à la psychométrie, elle approfondit la problématique de la mesure en psychologie selon deux perspectives.
Le titre développé de cette grande leçon est « Du qualitatif au quantitatif : théorie et applications ». Consacrée à la psychométrie, elle approfondit la problématique de la mesure en psychologie selon deux perspectives.
- D’une part, il s’agit d’expliciter la construction d’un observable comme le processus de composition d’applications, processus qui permet de transcrire des énoncés qualitatifs en énoncés quantitatifs.
- D’autre part, il s’agit de montrer comment l’utilisation des prévisions qu’il est possible de dériver statistiquement à partir des « sorties » de l’observation psychotechnique étaye l’intervention du psychologue dans des problématiques de dépistage, de sélection et de conseil.
1. Ordre simple
Objectifs . Introduire la notion d'ordre simple et l'appliquer au cas où les réponses à deux items de test sont analysées conjointement.
Prérequis.
Résumé. Les scores de tests sont fabriqués pour permettre une description des gens dans un ordre simple. Mais les scores ne décrivent pas les réponses des gens au test de manière adéquate, parce que ces réponses ne sont pas simplement ordonnées. Donc il est abusif de conclure de la simple existence du test que ce test permet de mesurer une grandeur psychologique, puisque pour qu'une grandeur psychologique puisse être mesurée, il faut déjà que l'on sache ordonner les réponses observées. Or les réponses observées sont définies dans un ensemble qui n'est pas simplement ordonné.
1.1. Introduction
Dans l'article Mesurage : logique et usage, nous avons considéré le problème qui consiste à transformer un vecteur de réponses en un score pour mimer un procédé de mesurage. Le procédé symbolique crée la grandeur à l'aide d'une règle de codage numérique des réponses aux items et d'une règle d'addition des nombres ainsi obtenus. Nous avons aussi esquissé la possibilité d'une autre attitude qui consiste à refuser d'attribuer un degré d'attachement au quartier à quiconque si cette grandeur n'est pas réelle. Pour développer une théorie de la grandeur en tant qu'hypothèse scientifique, il faut d'abord avoir une théorie de l'ordre dans l'espace d'échantillonnage du test.
Nous avons constaté que les auteurs s'intéressaient à l'attachement du point de vue ordinal : par exemple, il s'agit de savoir si "les femmes" sont plus attachées à leur quartier que "les hommes", mais pas de quantifier la différence. Dans un premier temps, nous allons étudier en quoi les scores obéissent à une logique ordinale. Ensuite, nous verrons en quoi cette logique ordinale constitue une hypothèse empirique testable lorsqu'on étudie les réponses aux items de l'échelle d'attachement au quartier.
1.2. La logique ordinale des scores
Une échelle de scores est un ensemble ordonné de nombres. Par exemple, les scores de l'échelle d'attachement au quartier sont compris dans l'ensemble {6, 7, ..., 30}. Cet ensemble, muni de la relation ≤, forme ce qu'on appelle un ordre simple et nous allons définir précisément ce qu'est un ordre simple. La relation ≤ est appelée une relation binaire parce qu'on forme des propositions de la forme a ≤ b, qui relient un terme (a) à un autre (b). Une relation binaire définie sur un certain ensemble est un ordre simple si elle possède les trois propriétés définitoires suivantes :
- La transitivité : soient trois nombres quelconques a, b et c de l'échelle des scores. Si a ≤ b et b ≤ c, alors a ≤ c.
Pour prouver que la relation ≤ est transitive sur l'échelle des scores, on peut vérifier que la proposition ci-dessus est vraie pour tous les triplets (a, b, c) possibles. Dénombrons-les. L'échelle comprend 30 - 5 = 25 scores. On a donc 25 choix pour le premier nombre. Ce choix étant effectué, on a aussi 25 choix pour le second nombre. Ce choix étant effectué, on a aussi 25 choix pour le troisième nombre. On a donc 25 3 = 15625 propositions à vérifier. Si on a a ≤ b et b ≤ c, alors on doit avoir a ≤ c. Sinon, peu importe.
- L'antisymétrie : soient deux nombres quelconques a et b de l'échelle. Si a ≤ b et b ≤ a, alors a = b.
Pour prouver que la relation ≤ est antisymétrique sur l'échelle des scores, on peut vérifier que la proposition ci-dessus est vraie pour tous les couples (a, b) possibles. On procède, comme précédemment, par un examen systématique de la validité des 25 2 = 625 propositions relationnelles possibles.
- La complétude forte (strong completeness) : soient deux nombres quelconques a et b de l'échelle. a ≤ b ou b ≤ a.
La preuve s'obtient aussi par vérification systématique (à défaut d'une stratégie mathématique plus économique).
Remarque : la complétude forte implique une autre propriété qu'on appelle la réflexivité : a ≤ a. Pour prouver cela, il suffit de remplacer b par a dans la définition de la complétude forte. La complétude tout court signifie que pour tout a ≠ b, a ≤ b ou b ≤ a.
Le problème qui se pose à présent est de savoir si l'ensemble des réponses au test peut être muni d'une relation qui permet de définir un ordre simple. En effet, le test permet d'observer des 6-uplets de réponses. Si le domaine des faits observables n'est pas un ordre simple, on ne peut pas déduire que c'est un ordre simple et l'échelle des scores ne représente pas correctement ce qui se passe dans la réalité à laquelle le questionnaire permet d'accéder.
Note. Par définition, le test ne permet pas d'accéder au vécu d'attachement au quartier. Il permet d'accéder à un monde de verbalisations possibles.
1.3. Exercice corrigé
On considère un test composé de deux items cotés dans {0, 1}. Définir l'échelle des scores S en considérant que le score compte le nombre de réponses correctes (cotées 1). Montrer que la relation ≤ définie sur S est un ordre simple. (Cette démonstration est très formelle, mais elle doit être acquise dans son principe pour aller plus loin avec des objets non numériques, comme, en particulier, des phénomènes observés en psychologie).
L'espace d'échantillonnage du test est E = {00, 01, 10, 11}. On obtient donc l'échelle S = {0, 1, 2}. La relation ≤ définie sur S est un ordre simple si elle est transitive, antisymétrique, et fortement complète.
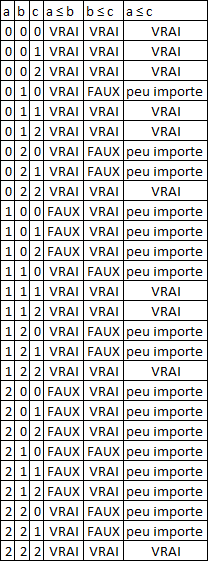
Transitivité : on considère les 3×3×3 triplets de nombres possibles et on vérifie que  et
et  , c'est-à-dire que si on a
, c'est-à-dire que si on a  et
et  , alors on a aussi
, alors on a aussi  . Les vérifications sont listées ci-dessous.
. Les vérifications sont listées ci-dessous.
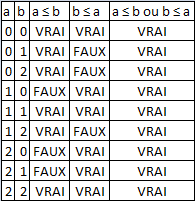
Antisymétrie : on considère les 3×3 couples de nombres possibles et on vérifie que  et
et  . Les vérifications sont listées ci-dessous.
. Les vérifications sont listées ci-dessous.

Complétude forte : on considère les 3×3 couples de nombres possibles et on vérifie que  ou
ou  . Les vérifications sont listées ci-dessous.
. Les vérifications sont listées ci-dessous.
La relation ≤ définie sur S est transitive, antisymétrique et fortement complète, donc c'est par définition une relation d'ordre simple.
1.4. Ordonner simplement des couples de valeurs simplement ordonnées
Nous allons beaucoup simplifier le problème sans perdre en généralité. Considérons que le test comprend non pas six mais deux items, et que les réponses sont recueillies sur une échelle de quatre degrés. Si on comprend la nature du problème qui se pose dans ce cas, on a des chances de comprendre le problème qui se pose pour le test initial.
L'espace d'échantillonnage des réponses à ce test à deux items est le produit cartésien
S = {1, 2, 3, 4} × {1, 2, 3, 4} = {(1, 1), (1, 2), ..., (4, 4)}.
Pour faciliter l'écriture, on notera (a, b) par ab. Le problème est donc de savoir comment on peut ordonner simplement l'ensemble S. Par exemple, comment peut-on ordonner 12 et 21 ? À notre connaissance, il n'existe pas de réponse adéquate à cette question. Si on ne peut pas ordonner 12 et 21, alors S n'est pas un ensemble simplement ordonné. Et donc le test n'est pas adapté à la mesure ordinale des personnes qui répondent à ce test.
Dans la section suivante, nous allons examiner la structure logique du test à l'aide de ce qu'on appelle la relation d'ordre produit direct (Barbut & Monjardet, 1970).
1.5. Ordre produit direct et diagramme de Hasse
On peut définir une relation binaire sur S, et la noter " ", de la manière suivante :
", de la manière suivante :
Il s'agit de ce qu'on appelle la relation d'ordre produit direct.
Cette relation est une relation d'ordre, parce qu'elle permet d'ordonner par exemple les couples 11 et 23. Mais ce n'est pas une relation d'ordre simple, parce qu'elle n'est pas complète. Autrement dit, il existe des paires d'éléments de l'ensemble S que la relation " " ne permet pas de comparer. Par exemple, les éléments 12 et 21 sont incomparables.
" ne permet pas de comparer. Par exemple, les éléments 12 et 21 sont incomparables.
Pour évaluer précisément l'ampleur du problème, testons la complétude forte en procédant comme dans l'exercice corrigé de la section 3. La liste ci-dessous identifie 72 cas d'incomparabilité.

Comme il existe 16×16 = 256 couples possibles, la probabilité logique d'incomparabilité est 72/256, soit environ 28%.
Pour représenter graphiquement cette relation d'ordre, on peut utiliser ce qu'on appelle un diagramme de Hasse, comme l'illustre la figure ci-dessous :
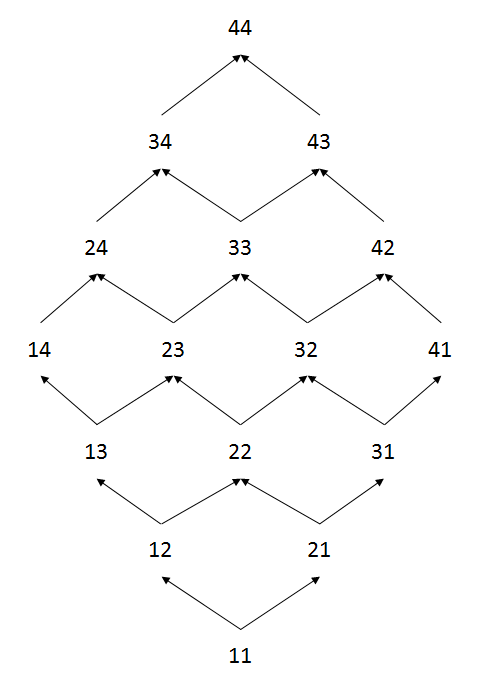
L'organisation en couches du diagramme montre que les éléments distincts d'une même couche ne sont pas comparables. Elle montre aussi que des éléments provenant de deux couches différentes ne sont pas nécessairement comparables. Par exemple, 12 et 31 ne sont pas comparables, parce que 1 > 3 et 2 < 3 (il suffit que les signes < et > soient présents quand on compare les composantes pour que les vecteurs soient incomparables). On peut aussi visualiser le concept de chaîne, c'est-à-dire de sous-ensemble qui constitue un ordre simple. Par exemple, le sous-ensemble {11, 12, 22, 32, 42, 43, 44} constitue une chaîne.
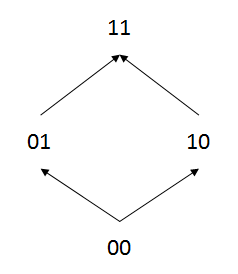
1.6. Exercice corrigé (n°2)
On considère un test de deux items cotés dans {0, 1}. Tracer le diagramme de Hasse associé au test. L'espace d'échantillonnage du test est E = {00, 01, 10, 11}. En munissant E de la relation d'ordre produit direct " ", on peut constater que 01 et 10 forment l'unique paire d'éléments incomparables. Le diagramme de Hasse associé à cette relation est tracé ci-dessous.
", on peut constater que 01 et 10 forment l'unique paire d'éléments incomparables. Le diagramme de Hasse associé à cette relation est tracé ci-dessous.
1.7. Conclusion
Cet article pose le problème suivant : si un test est fondé sur k>2 items dont les réponses sont simplement ordonnées et si ce test est fait pour mesurer une grandeur, alors les événements que le test peut enregistrer doivent être simplement ordonnés. C'est par exemple ce qui se passe avec un thermomètre : le liquide dont la hauteur indique les variations de température ne peut que monter, descendre, ou rester sur place. Or les événements que le test permet d'observer sont des vecteurs, qu'on peut ordonner à l'aide de la relation d'ordre produit direct, mais c'est un fait mathématique que l'ensemble des vecteurs n'est pas simplement ordonné par cette relation d'ordre (autrement dit, l'ordre est incomplet). Par conséquent, la conception logique du test est en contradiction avec sa fonction.
Le psychologue qui souhaite mesurer l'attachement au quartier dans une perspective scientifique doit donc ne pas accepter les scores comme des mesures ordinales puisqu'elles contredisent la structure logique des événements qu'elles sont supposées représenter. Une possibilité théorique consiste à supposer que certains événements possibles ne sont jamais observés précisément parce que les réponses obéissent à une loi d'ordre simple. Ce type de réflexion est développé dans l'article "Tester qu'une description multivariée permet un mesurage ordinal".
2. La confusion nominale induite par les scores psychométriques
Objectifs. À l'aide d'un exemple, montrer en quoi l'interprétation empirique d'un score de test soulève un problème de cohérence opératoire.
Prérequis.
Résumé. L'utilisation des nombres peut être logiquement absurde, en particulier lorsqu'on applique des transformations numériques qui ne représentent rien dans l'ensemble des événements empiriques associés à ces nombres.
2.1. Un exemple
Considérons un test composé de quatre items cotés dans (0, 1). Le score au test est calculé en sommant les scores aux items.
La signification opératoire (ou empirique) du score total 1 est que les réponses apportées sont contenues dans l'ensemble suivant :
{0001, 0010, 0100, 1000}.
La signification opératoire du score total 2 signifie que les réponses ont été obtenues dans l'ensemble suivant :
{0011, 0101, 0110, 1001, 1010, 1100}.
2.2. "1 = 1" : vrai, mais aussi "1 = 1" : faux
Lorsqu'on écrit "1 = 1" en se référant à la signification opératoire du score, on dit la vérité dans 4 cas sur 16 (i.e., on ment dans 12 cas sur 16).
| 0001 |
0010 | 0100 |
1000 | |
| 0001 |
= |
|||
| 0010 | = |
|||
| 0100 |
= |
|||
| 1000 | = |
Le problème des mensonges est réglé si on décide de confondre toutes les réponses -- sans justification théorique. C'est ce que nous appelons la solution de la confusion nominale.
2.3. "1 ≤ 2" : vrai, mais aussi "1 ≤ 2" : faux
Lorsqu'on écrit "1 ≤ 2" en se référant à la signification opératoire du score, si on s'appuie sur l'ordre produit direct dans l'ensemble des réponses, on dit la vérité dans 12 cas sur 24 (i.e., on ment dans la moitié des cas).
| 0011 | 0101 | 0110 | 1001 |
1010 |
1100 |
|
| 0001 | ≤ | ≤ |
≤ | |||
| 0010 | ≤ | ≤ | ≤ | |||
| 0100 | ≤ | ≤ | ≤ |
|||
| 1000 | ≤ | ≤ | ≤ |
Le problème des mensonges est aussi réglé par la confusion nominale. En effet, on peut toujours substituer un terme de manière à pouvoir rendre deux termes comparables.
2.4. Conclusion
Lorsqu'on utilise des scores psychométriques pour décrire ce qui se passe dans un champ phénoménal public, c'est-à-dire dans le référentiel de description des réponses au test, on utilise une logique descriptive qui n'est pas fiable. D'où le choix suivant :
- soit on abandonne le langage descriptif des scores, ce qui signifie qu'on admet la possibilité que certaines réponses ne soient pas comparables,
- soit on veut à tout prix que toutes les réponses soient comparables, et alors il faut proposer une convention pour projeter les descriptions sur une ligne (i.e., un ensemble simplement ordonné). Mais alors, tous les utilisateurs, y compris les personnes évaluées, sont, en principe, habilités à voter pour ou contre cette convention. Si ce n'est pas le cas, l'utilisation des scores psychométriques est une forme de domination politique, en ce sens que quelqu'un exerce le pouvoir de donner un statut à quelqu'un d'autre dans une échelle de valeurs, sans que cela puisse être remis en cause. Dans cette perspective, le testage psychologique constitue une institution sociale dont les fondements scientifiques et philosophiques sont douteux.
3. Risque et facteurs de risque

Objectifs. Définir les notions de risque, de facteur de risque, et d'échelle de risque.
Prérequis.
Résumé. Le risque est une possibilité. Un facteur de risque est une condition pour laquelle l'événement auquel on s'intéresse (par exemple, le suicide) est plus possible que lorsque cette condition n'est pas réalisée. On peut mesurer cette possibilité en se ramenant au schéma d'une urne dans laquelle se trouvent des spécimens décrits de différents points de vue (descripteurs) et en utilisant la fréquence conditionnelle de l'événement étudié. Cette approche n'est pas causale, mais descriptive. La compréhension causale d'un événement nécessite une approche historique et non pas statistique.
3.1. Le risque comme possibilité
Le risque désigne la possibilité. On peut dire "la possibilité de gagner au loto" comme "le risque de gagner au loto" (si je ne joue pas, je ne risque pas de gagner). On pourrait aussi suggérer de réserver l'emploi du terme lorsque ce qui est possible est un événement (ou une situation) indésirable. Mais ce qui est indésirable pour l'un peut être désirable pour l'autre, donc ce n'est pas une bonne idée tant qu'on ne veut pas compliquer les choses en spécifiant qui s'intéresse au risque d'un certain événement.
La possibilité d'un événement est une notion logiquement binaire : soit elle existe, soit elle n'existe pas (elle est nulle). Par exemple, la possibilité que je gagne au loto n'existe pas si je ne joue pas. En pratique toutefois, on souhaite évaluer la possibilité dans une perspective ordinale ou bien quantitative -- la probabilité d'un événement est, disons, de 70%. La question est alors de savoir comment mesurer ce risque (quelle que soit la perspective de mesurage).
Dans tous les cas, il va donc falloir spécifier les conditions dans lesquelles on veut évaluer (ou mesurer) la possibilité d'un événement. D'où l'importance d'une théorie de ce qui détermine (ou conditionne) l'événement, même si cette théorie est partielle.
3.2. Conditions et ordre partiel
Prenons l'exemple du risque suicidaire ; on s'intéresse à la possibilité que quelqu'un se suicide. Par exemple, on considère :
- C1 : l'envie de se suicider (oui = 1, non = 0),
- C2 : le fait de connaître le "pont des suicidés", un pont d'où se sont jetées plusieurs personnes (oui = 1, non = 0).
On définit l'application 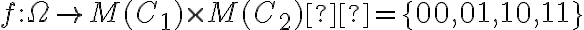 qui, à toute personne âgée de plus de 12 ans évaluée à une certaine date, associe une certaine condition dans cet ensemble. Comment ordonner ces conditions du point de vue de l'acte qui consiste à se jeter dans le vide du haut de ce pont (sans élastique) ? 00 et 11 sont les extrema de cet ensemble, respectivement le minimum et le maximum. La question est de savoir si on peut ordonner les couples 01 et 10.
qui, à toute personne âgée de plus de 12 ans évaluée à une certaine date, associe une certaine condition dans cet ensemble. Comment ordonner ces conditions du point de vue de l'acte qui consiste à se jeter dans le vide du haut de ce pont (sans élastique) ? 00 et 11 sont les extrema de cet ensemble, respectivement le minimum et le maximum. La question est de savoir si on peut ordonner les couples 01 et 10.
Ce mode de suicide est-il plus possible pour quelqu'un qui n'a pas envie de se suicider et qui connaît le pont des suicidés que pour quelqu'un qui a envie de se suicider et qui ne connaît pas ce pont (i.e., a-t-on 01 > 10) ? Nous ne voyons pas de raison de répondre par l'affirmative. De même, nous ne voyons pas pourquoi on pourrait affirmer 10 > 01. Bien entendu, nous avons négligé d'autres modes opératoires du suicide, et il conviendrait de commencer par en faire la liste.
Nous voulons montrer par cet exemple qu'étant donné un certain ensemble fini de conditions possibles, y compris les modes opératoires du suicide, il est douteux que cet ensemble puisse être simplement ordonné (voir Ordre simple) du point de vue de l'intuition d'une échelle de degrés de possibilité du suicide. Autrement dit, si on définit un ensemble de conditions possibles, dont la structure peut être très complexe étant donné que les circonstances d'un suicide sont ancrées dans des histoires individuelles, il est douteux que cet ensemble puisse être simplement ordonné.
La compréhension de l'acte de suicide relève de l'enquête policière et en pratique, les travailleurs sociaux, au sens large, sont confrontés à des contraintes matérielles (et peut-être psychologiques) qui les empêchent d'étudier minutieusement ce qui rend possible qu'une personne donnée se suicide selon tel ou tel mode opératoire. D'où la notion statistique de facteur de risque (suicidaire).
3.3. Facteurs de risque
La notion de facteur de risque se fonde sur la notion de fréquence conditionnelle de l'événement auquel on s'intéresse. Par exemple, on s'intéresse à un grand groupe de personnes qui, étant donnée une certaine date t , se sont suicidées ou pas avant cette date. Le risque de suicide est la fréquence (ou proportion) des cas de suicide dans ce groupe.
Considérons la caractéristique "sexe". On s'intéresse maintenant à la fréquence des suicides parmi les hommes. Si cette fréquence est supérieure à la fréquence des suicides dans le groupe total, alors le fait d'être un homme est un facteur de risque (si cette fréquence est inférieure, on trouve parfois l'expression "facteur de protection" qui est abusive parce qu'elle suggère une relation causale -- une influence -- entre le sexe et le suicide).
Considérons la caractéristique "dépression" en admettant qu'elle soit binaire. On s'intéresse maintenant à la fréquence des suicides parmi les personnes déprimées (quel que soit leur sexe).Si cette fréquence est supérieure à la fréquence des suicides dans le groupe total, alors le fait d'être déprimé est un facteur de risque.
De fil en aiguille, on est amené à l'idée qu'il devrait être possible d'ordonner les différentes conditions dans lesquelles peuvent se trouver les personnes du groupe en fonction des fréquences conditionnelles de suicide.
3.4. La construction d'une échelle de risque
Tout d'abord, les considérations qui précèdent montrent que la notion d'échelle de risque n'a pas de sens si on ne dispose pas d'une description de l'événement risqué. Une façon simple de garder ce point à l'esprit est de toujours se demander "risque de quoi", ou bien "fréquence de quoi". Si un article scientifique présentait une échelle de risque fondée par exemple sur des scores psychométriques, l'idée principale étant que plus le score est élevé, plus le risque est grand, cette échelle ne serait pas une échelle de risque parce qu'on ne pourrait pas connaître la fréquence de l'objet du risque conditionnellement aux scores. Quant à l'interprétation propensionniste d'un score psychométrique -- la propension au suicide --, il s'agit tout simplement d'une forme d'occultisme moderne, puisque la propension au suicide signifie la tendance à se suicider et que la mesure d'une tendance à adopter un certain comportement suppose de compter combien de fois ce comportement est adopté dans un grand nombre de "situations test".
C'est ici qu'on voit clairement les glissements de sens qui peuvent s'opérer en la matière : il n'est pas possible de mesurer la propension au suicide (réussi) d'une personne, parce que ce serait une fréquence individuelle. D'où la tentation de prendre les fréquences inter-individuelles comme des fréquences intra-individuelles, ce qui permet d'attribuer la propriété à toute personne du groupe de référence. Mais ce raisonnement est fallacieux, car la fréquence est une propriété du groupe -- elle change si on change le groupe -- alors que la propension est par définition une propriété individuelle. Quant à parler de propension du groupe, la fréquence des suicides dans le groupe ne permet pas d'évaluer la propension de l'agrégat de personnes considérées à se suicider collectivement... (cf. Mesurage : logique et usage).
Une échelle de risque est foncièrement une liste ordonnée de fréquences conditionnelles. Par exemple, considérons les données fictives suivantes. On s'intéresse au taux de tentatives de suicide ratées dans le mois qui précède une enquête. Les personnes enquêtées sont connues du point de vue de leur sexe (1 = homme, 2 = femme), de leur tranche d'âge (1 pour les jeunes adultes (18 à 34 ans), 2 pour les adultes (35 à 64 ans), 3 pour les âgés). Les conditions dans lesquelles on peut se suicider sont données par le produit cartésien
{1, 2} × {1, 2, 3} = {11, 12, 13, 21, 22, 23},
soient un ensemble de six conditions différentes.
On trouve les fréquences suivantes pour chaque groupe, les groupes étant classés par ordre croissant des fréquences conditionnelles :
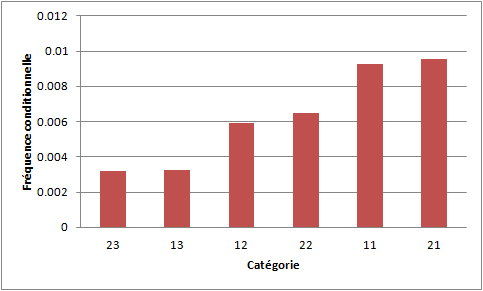
La catégorie d'âge, plus exactement le fait d'être jeune, est un facteur de risque, puisque les TS (tentatives de suicide ratées) sont les moins fréquentes dans les groupes de personnes âgées (13 et 23), un peu plus fréquentes dans les groupes des adultes (12 et 22) et un peu plus fréquentes dans les groupes des jeunes adultes (11 et 21). Le sexe n'est pas un facteur de risque puisque quelle que soit la catégorie d'âge, le taux de TS est approximativement le même pour les hommes et les femmes. Dans cet exemple, l'échelle de risque est une échelle en trois niveaux d'âge.
La fréquence des TS peut être analysée en fonction de caractéristiques psychologiques. Par exemple, considérons les réponses aux trois questions suivantes : au cours du dernier mois écoulé, avez-vous :
- pensé qu’il vaudrait mieux que vous soyez mort(e), ou souhaité être mort(e) ? (oui = 1, non = 0)
- voulu vous faire du mal ? (oui = 1, non = 0)
- pensé à vous suicider ? (oui = 1, non = 0)
Le référentiel de description associé est l'ensemble {000, 001, 010, 011, 100, 101, 110, 111}.
On trouve les fréquences suivantes pour chaque groupe, les groupes étant classés par ordre croissant des fréquences conditionnelles :
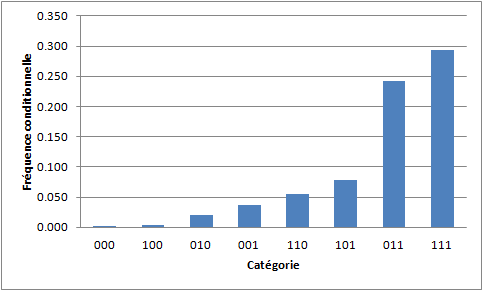
Cette fois-ci, les résultats sont plus intéressants, puisque les catégories (ou conditions) 011 et 111 ont une fréquence de TS supérieure à 20%. De plus, on remarque que le niveau de risque de la conjonction des faits "avoir voulu se faire du mal" et "avoir pensé à se suicider" (011) est nettement plus élevé que la somme des niveaux de risque des faits "avoir voulu se suicider" (010) et "avoir pensé à se suicider" (001). Autrement dit, les facteurs de risque ne sont pas additifs.
Nous terminerons cette présentation par deux remarques.
- Les fréquences conditionnelles sont calculées pour chaque condition. Si on ajoute des descripteurs (addition), le nombre de conditions augmente de manière multiplicative car les conditions sont les éléments du produit cartésien des modalités des descripteurs. Par exemple, si on ajoute le sexe, l'âge, le fait d'avoir déjà fait une TS aux descripteurs de cette échelle, on obtient 2 × 3 × 2 × 8 = 96 conditions qui sont des 6-uplets de valeurs. Mais le nombre d'observations reste identique et on augmente les chances que les groupes de référence aient des effectifs faibles. Si c'est le cas, les fréquences conditionnelles ne seront pas stables d'un échantillon à un autre et l'échelonnement des catégories en fonction des fréquences de l'événement étudié ne sera pas stable non plus. Le constructeur d'une échelle de risque doit donc naviguer entre deux écueils : la pauvreté descriptive de son échelle et la robustesse de ses estimations de niveau de risque.
- Une échelle de risque ne permet pas un pronostic individuel, puisque pour faire un pronostic individuel, il faut connaître la propension de l'individu (ici, à tenter de se suicider en se ratant). Une interprétation causale des niveaux de risque ainsi échelonnés est donc toujours abusive d'un point de vue scientifique (cf. le paragraphe 2 et aussi l'article La prédiction scientifique et actuarielle).
4. Tester qu'une description multivariée permet un mesurage ordinal
Objectifs. Spécifier et illustrer une démarche générale de recherche en psychométrie appliquée au mesurage ordinal.
Prérequis.
Résumé. Si la psychométrie est la science du mesurage psychologique, faire de la recherche en psychométrie consiste à formuler l'hypothèse qu'une description particulière permet de mesurer une grandeur, au minimum de manière ordinale. Avec la logique et l'observation, cela est possible, en suivant une démarche générale qui distingue (1) l'analyse théorique des descriptions disponibles, (2) la formulation des hypothèses de mesurage, et leur test empirique.
4.1. Le problème
De nombreux tests ou questionnaires psychologiques sont fondés sur plusieurs items, disons k items. Par conséquent, la réponse prend la forme d'un vecteur de k composantes, ou encore d'un k-uplet.
On a vu dans l'article "Ordre simple" qu'un tel langage descriptif est logiquement incompatible avec un langage comparatif (i.e., tel qu'une description quelconque soit plus petite, ou plus grande que, ou encore égale à une autre description quelconque), parce qu'il existe dans le référentiel du test au moins deux vecteurs qui sont différents, mais dont on ne peut pas affirmer que l'un est plus petit ni plus grand que l'autre en se référant à la notion d'ordre produit direct.
Cette incompatibilité logique n'est pas nécessairement pertinente du point de vue théorique. En effet, on peut supposer que les phénomènes qu'on peut décrire dans le référentiel du test obéissent à un ordre simple, et tester cette hypothèse par le raisonnement et l'observation.
4.2. Un exemple : l'anxiété est une grandeur mesurable avec deux items
Considérons les items "Je me fais du souci" et "Je me sens tendu(e)", assortis des choix de réponse "non" et "oui". Comme les réponses suggèrent respectivement l'absence et la présence d'anxiété, on peut les coter 0 et 1. Les réponses à tout item sont simplement ordonnées.
Pour spécifier la théorie selon laquelle les réponses aux deux items mesurent l'anxiété, il faut d'abord spécifier comment on relie le référentiel de l'anxiété au référentiel de tout item. Le référentiel de l'anxiété est un intervalle de la forme [0, max]. Il faut admettre l'existence d'une origine qui correspond à l'absence d'anxiété dans le psychisme de la personne qui répond. On exclut aussi la possibilité d'une quantité négative d'anxiété. Enfin, on admet l'existence d'une quantité maximale d'anxiété, au-delà de laquelle la personne n'est plus en état de répondre.
Nous ne connaissons pas d'autre moyen pour spécifier la relation entre [0, max] et {0, 1} qu'une fonction par palier, ou encore une fonction à seuil. Appelons ce seuil
s. Quand la quantité d'anxiété varie dans [0,
s
[, la réponse est 0. Quand la quantité d'anxiété varie dans [
s
, max[, la réponse est 1. On obtient la courbe représentative ci-dessous.
Cette façon d'interpréter la réponse à un item est tautologique, puisqu'on ne peut pas mesurer l'anxiété sans la réponse à l'item. Si on considère les deux items, alors on déduit trois théories testables.
La première théorie est que le seuil du premier item se trouve avant le seuil du second item. Dans ce cas, on obtient la fonction suivante :
Cette théorie possède un falsificateur, à savoir l'observation 01, qui signifie que la personne a répondu non à l'item 1 et oui à l'item 2. Si elle a répondu non à l'item 1, sa quantité d'anxiété est inférieure au seuil de l'item 1, donc elle ne peut pas être supérieure au seuil de l'item 2, qui se trouve par hypothèse après le seuil de l'item 1. Or, elle a répondu oui à l'item 2, ce qui signifie que sa quantité d'anxiété est supérieure au seuil de l'item 2. Comme l'observation est vraie (on exclut une erreur de la part de celui qui rapporte les réponses par exemple), c'est que la théorie est fausse.
La deuxième théorie est que le seuil de l'item 1 se trouve après le seuil de l'item 2. Nous laissons au lecteur le soin de tracer la fonction correspondante. Le falsificateur de la théorie est l'observation 10, pour des raisons analogues à celles que nous venons d'exposer pour la théorie n° 1.
Enfin, la troisième théorie est que les seuils des deux items se trouvent au même endroit dans [0, max[. Elle possède deux falsificateurs, à savoir les observations 01 et 10.
4.3. Fonctions non injectives
Une fonction par palier ne permet pas de déterminer la quantité d'anxiété de manière exacte. Par exemple, si on se réfère à la première fonction de la section précédente, le fait de savoir que la réponse est 00 permet seulement de savoir que la quantité d'anxiété se trouve dans l'intervalle [0, seuil de l'item 1[. Du point de vue mathématique, cela revient à dire que la fonction n'est pas injective. (Pour un rappel de maths sur la notion d'injectivité, voir l'article "Injection, surjection, bijection".)
On peut augmenter la précision du mesurage en augmentant le nombre de paliers, c'est-à-dire en augmentant le nombre de modalités de réponses et/ou le nombre d'items.
4.4. Conséquences théoriques de la falsification
Un chercheur teste une personne en maintes occasions et observe que les réponses falsifient les trois théories. Alors les trois théories sont fausses. Il n'est pas correct d'affirmer que tout se passe comme si la personne répondait selon un principe -- une fonction par palier -- qui permet d'interpréter ses réponses comme des mesures ordinales sur une échelle à deux (théorie 3) ou trois degrés (théories 1 et 2).
La falsification des trois théories implique que les réponses dépendent d'autre chose que de la quantité hypothétique, celle-ci pouvant soit ne pas exister, ou bien exister néanmoins. Il faut alors concevoir le mécanisme multifactoriel de la production des réponses. Par exemple, la personne pourrait penser "ah, oui, je me fais du souci pour ce problème de porte qui ne ferme pas, mais ça n'est pas de l'anxiété ça, donc, je réponds non". Dans ces conditions, la réponse à l'item dépend d'un phénomène cognitif et, si on tient à la fonction par palier, force est d'admettre qu'elle est en quelque sorte "off". Le problème est qu'on ne voit pas comment se débarrasser des cognitions, puisque le principe même d'un item de questionnaire auto-évaluatif est qu'il repose sur la capacité des gens à s'auto-évaluer, i.e., à produire des cognitions sur eux-mêmes.
Une autre conséquence est que si on a falsifié les théories possibles avec deux items, il ne sert à rien de rajouter d'autres items. Si le mesurage "marche" avec n items, il "marche" avec n-1 items (n-1 n'étant pas plus petit que 2). Si on ajoute des items, on augmente le nombre de degrés (exactement, d'intervalles) de l'échelle de mesure, mais ces degrés n'ont de sens que si une fonction par palier est testée et corroborée.
4.5. Conséquences pratiques de la falsification
Si on ne dispose pas d'un principe théorique pour interpréter les réponses comme des mesures ordinales d'une quantité hypothétique, on doit se contenter de ne pas interpréter les données en référence à une grandeur hypothétique, dont on sait qu'on ne sait pas la mesurer.
Cela n'empêche pas, lorsque cela est possible, de constater une "amélioration" ou une "détérioration" du tableau clinique, si les vecteurs sont comparables. Si les vecteurs ne sont pas comparables, on ne peut que constater une évolution non-ordinale. Autrement dit, c'est au psychologue de rejeter la pertinence empirique d'un construit quantitatif comme l'anxiété.
5. Classer des candidats

Objectifs. Spécifier et illustrer le problème du classement d'un ensemble de candidats décrits de manière multivariée.
Prérequis.
Résumé. Le classement des candidats décrits selon plusieurs scores psychométriques est sensible à la manière dont on pondère la somme des scores pour établir le classement. D'où le problème, sans solution, de la justification des poids utilisés. Si on considère que le meilleur candidat est celui est qui le meilleur à tous les tests, on peut utiliser le principe du rang maximum pour classer les candidats sans faire appel à une somme pondérée des scores.
5.1. Le problème
Les tests psychologiques sont parfois utilisés pour classer des candidats lorsqu'on ne dispose pas d'un critère de classement. L'idée générale est que plus un candidat a une performance élevée au test, mieux il doit être classé. Si les performances aux tests sont décrites dans un format vectoriel, il n'est a priori pas garanti que les candidats puissent être classés, c'est-à-dire placés dans un ordre simple. La méthode usuelle consiste à calculer un score psychométrique, et les candidats sont alors classés en fonction de leur score (avec d'éventuels ex aequo). Lorsque les candidats sont décrits par plusieurs scores, la méthode usuelle consiste à calculer une somme pondérée des scores (on dit aussi une combinaison linéaire des scores). Les candidats sont alors classés en fonction de leur somme.
Le problème qui se pose est que les pondérations d'une combinaison linéaire des scores n'ont pas de signification opératoire claire. Par conséquent, le classement obtenu à l'aide d'une combinaison linéaire donnée n'est pas meilleur que le classement qui serait obtenu avec une autre combinaison linéaire. Comment choisir la "bonne" combinaison linéaire ? Nous allons exposer une méthode de classement fondée sur une interprétation ordinale des scores, qui permet d'éviter l'utilisation d'une combinaison linéaire.
Auparavant, il faut comprendre ce qui se passe et nous allons utiliser un exemple. Paul a obtenu les scores x A = 1,5 au test A et x B = -0,5 au test B, tandis que Julie a obtenu les scores y A = 1 et y B = 0,3. Ces scores sont considérés comme des mesures d'intervalle, c'est-à-dire qu'on considère qu'on sait mesurer la distance entre deux scores au même test. Savoir mesurer la distance entre deux scores signifie que n'importe quelle transformation affine positive des scores est valable (voir l'article Échelles de mesure).
Multiplions les scores au test A par la valeur strictement positive a, et ajoutons la valeur b. La différence entre les scores de Paul et Julie à ce test est multipliée par a (a est factorisé et b s'annule). Les différences entre scores mesurés sur une échelle d'intervalle sont mesurées sur une échelle de rapport. En effet, le rapport de deux différences ne change pas, quelles que soient les valeurs a et b qu'on utilise lorsqu'on applique une transformation affine positive (i.e., a > 0) aux scores du test.
Les pondérations qu'on introduit dans la combinaison linéaire des scores sont donc arbitraires du point de vue de la signification psychométrique des scores, puisqu'elles sont des transformations affines positives. Mais elles ne sont pas sans effet sur les classements. Par exemple, si on compare la somme des scores de Paul et celle de Julie, Paul obtient 1 et Julie obtient 1,3, donc Julie est "meilleure". Mais si on double les scores au test A, ce que rien ne nous interdit de faire, et qu'on fait ensuite la somme, Paul obtient 2,5 et Julie obtient 2,3, donc Paul est "meilleur". On montre que la comparaison reste invariante si et seulement si les vecteurs des scores sont comparables (au sens de l'ordre produit direct).
On peut alors préférer une méthode de classement qui ne dépend pas d'une combinaison linéaire des scores et qui, si elle ne produit pas trop d'ex aequo, pourra être utilisée à la place de la méthode usuelle si le problème des pondérations se pose d'une manière ou d'une autre (en pratique, comme les gens qui sont classés ignorent ce type de choses et font confiance aux évaluateurs, le problème n'est pas "mis sur la table").
5.2. Le principe du rang maximum
Prenons l'exemple de 16 candidats qui ont passé deux tests. Le meilleur serait celui qui est le meilleur au premier test et le meilleur au second test, c'est-à-dire qui aurait les rangs 1 et 1, ce qu'on note 11. S'il existe, on le classe premier. Ensuite, on considère les cas "12" (premier rang au test A, deuxième rang au test B), "21" et "22". Autrement dit, on considère les cas de rang maximum 2. Et ainsi de suite jusqu'à avoir "attrapé" tous les cas. À chaque fois qu'on considère un rang maximum, on définit une classe. La classe 1 contient les cas 11, la classe 2 contient les cas 12, 21 et 22 (mais pas les cas 11). La classe 3 contient les cas 13, 23, 33, 31, 32, 33, etc.
Visuellement, la méthode consiste à progresser par couches successives sur le plan représenté ci-dessous. Chaque point représente un candidat. La première couche identifie un candidat dont le rang maximum est 7. La seconde couche identifie un candidat dont le rang maximum est 8. La troisième couche identifie deux candidats dont le rang maximum est 9. Le lecteur pourra compléter tout seul.
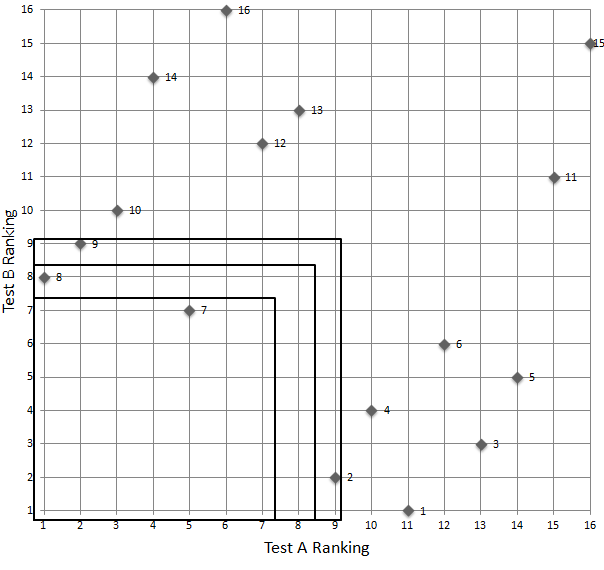
5.3. Classer les ex aequo
D'une manière générale, la méthode est applicable à des vecteurs de k rangs. Lorsqu'une classe contient plusieurs candidats, la méthode peut encore être appliquée à l'intérieur de la classe, en recherchant les rangs maximaux sur les k-1 dimensions qui n'ont pas le rang de la classe.
Ci-dessous par exemple, on peut voir que les cas, décrits par des triplets de rangs, qui ont été "capturés" dans une classe sont, à l'intérieur de cette classe, rangés selon le rang maximum des deux dimensions restantes. Le rang de la classe a été retiré des données pour le calcul du rang maximal.

6. Évaluer un changement
Objectifs. Montrer comment on peut représenter un changement décrit vectoriellement.
Prérequis.
Résumé. La description du changement à l'aide de scores psychométriques implique que le changement ne peut pas être conçu autrement que dans le cadre d'une amélioration, d'une détérioration ou d'une absence de changement. Or cette façon de décrire n'est pas adaptée au caractère multivarié, ou vectoriel, des descriptions initiales. On peut décrire les changements en comptant le nombre d'améliorations, le nombre de détériorations et le nombre de non-changements.
La description du changement d'un état clinique est un problème de représentation. L'usage en psychométrie consiste à décrire les états cliniques à l'aide d'un score psychométrique, qu'on interprète comme une mesure plus ou moins valide et fidèle d'une grandeur latente (comme l'anxiété par exemple). La différence des scores s'interprète alors comme une mesure plus ou moins valide et fidèle du changement.
Cette approche, quoiqu'elle soit très répandue, pose deux questions fondamentales : que mesure-t-on ? comment évaluer l'erreur de mesure ? A notre avis, il n'existe pas de réponse scientifiquement satisfaisante à ces questions. Notre approche consiste à constater que ces questions se posent parce que la démarche évaluative se fonde sur une hypothèse fondamentale qui est fausse, ou non testable : les scores mesurent des grandeurs. La conséquence de cette hypothèse est que le changement ne peut être conçu que dans un cadre de référence trivalué : soit l'état clinique s'améliore, soit il se détériore, soit il reste stable.
L'analyse logique des méthodes descriptives multivariées montre que les états cliniques sont les éléments d'un ordre incomplet, par opposition à un ordre simple. Un ensemble doté d'une relation d'ordre est un ordre incomplet s'il existe deux éléments qui ne peuvent pas être ordonnés l'un par rapport à l'autre par cette relation d'ordre (deux éléments incomparables, qui ne sont pas en relation l'un avec l'autre). La conséquence conceptuelle d'une telle analyse est que le langage des scores n'est pas adapté à la réalité des phénomènes qu'on est capable de décrire.
Les psychologues peuvent apprendre à manipuler non pas des scores, mais des vecteurs. Par exemple, considérons une description fondée sur 10 signes cliniques, qu'on cote de manière binaire (0 pour absence du signe, 1 pour présence du signe). On analyse le changement qui est intervenu entre une première observation
0 0 1 0 1 1 1 0 0 1
et une seconde observation
0 0 0 0 1 1 0 1 0 0.
Si on applique la relation d'ordre produit direct, on conclut à un cas d'incomparabilité. Mais on peut aussi résumer le changement de la manière suivante. On compte le nombre d'améliorations, c'est-à-dire le nombre de signes qui disparaissent, puis le nombre de non-changements, puis le nombre de détériorations, c'est-à-dire le nombre de signes qui apparaissent.
L'analyse du changement donne le vecteur suivant :
0 0 1 0 1 1 1 0 0 1
0 0 0 0 1 1 0 1 0 0
= = + = = = + - = +,
qui contient trois améliorations (les "+"), six non-changements (les "=") et une détérioration (le "-"). La description vectorielle du changement est donc (3, 6, 1). Le clinicien peut ainsi, d'un seul coup d'œil, constater que l'état clinique est plutôt stable (6/10) et plutôt amélioré (3/4) pour ce qui concerne les variations observées.
7. Questionnaire d'auto-évaluation
Ce QCM comprend 10 questions. Répondez à chaque question puis, à la fin, lorsque vous aurez répondu à toutes les questions, un bouton "terminer" apparaîtra sur la dernière question. En cliquant sur ce bouton, vous pourrez voir votre score et accéder à un corrigé.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte