Statistique descriptive
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L1 |
| Livre: | Statistique descriptive |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 21 février 2026, 23:10 |
Description
 Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Cette troisième grande leçon présente l'ensemble des concepts de base nécessaires à la description quantifiée d'observations. Elle constitue le vrai cœur de l'enseignement de la Statistique en L1 et l'étudiant y retrouvera exposés les principaux concepts qu'il aura vus dans ses cours. Toutefois, nous n'aborderons pas ici les aspects analytiques de l'inférence statistique, c'est-à-dire les concepts et méthodes permettant d'évaluer la fiabilité des résultats descriptifs et pour lequel nous renvoyons l'étudiant au cours de L2.
Rédaction : Éric Raufaste
Table des matières
- 1. introduction de la leçon
- 2. Indices de tendance centrale
- 3. Indices de dispersion
- 4. Représentations graphique des distributions
- 5. Quelques distributions statistiques remarquables
- 6. Techniques de recodage des données
- 7. Dépendances et causalité
- 8. Liaison entre deux variables
- 9. Prédire une variable numérique : la régression simple
- 10. Questionnaire d'auto-évaluation
1. introduction de la leçon
Dans la plupart des sciences empiriques, les statistiques sont au cœur de la méthode expérimentale. Elles font partie du cursus de psychologie dès la première année. Elles ont en effet une grande utilité pratique, et sont indispensables à la recherche fondamentale en psychologie (cognitive, développementale, sociale, et même clinique), mais aussi en sociologie, en économie, en biologie, et même en physique.
Tout d'abord, étudier la statistique permet une ouverture conceptuelle quant à la nature construite des connaissances, et sur les limites des conventions sur lesquelles repose la construction des connaissances. Pour autant, les statistiques constituent avec la biologie l’un des principales difficultés pour les étudiants en psychologie de L1 à L3. C'est pourquoi le but concret de ce cours de statistique pour les étudiants de L1 en sciences humaines est de fournir un complément aux cours qu'ils peuvent recevoir dans les cursus présentiels afin de les aider à s'approprier des concepts très abstraits et souvent formalisés à l'aide d'un symbolisme mathématique qui peut en rebuter certains. Il ne s'agit pas de faire l'impasse sur ces formalismes, mais plutôt de les expliquer, de les rendre accessibles à tous, ou presque.
Plan de la Grande Leçon "Statistique Descriptive"
Dans cet article, après la présente section d'introduction, nous commencerons par évoquer quelques définitions générales, en particulier la distinction entre LA statistique (en tant que science) et LES statistiques (en tant qu'objets produits par les méthodes issues de cette science). Dans un second temps, nous expliquerons la différence essentielle qui existe entre les statistiques descriptives, au programme du L1, et les statistiques inférentielles, au programme du L2.
L'article suivant sera consacré aux différents types de nombres. Ces types de nombres déterminent les opérations qu'il est légitime de réaliser et sont donc d'une importance cruciale pour le choix des statistiques descriptives comme inférentielles que l'on utilisera.
Le troisième article sera centré sur la notion de distribution statistique. Différents types de distributions seront présentés afin d'illustrer différentes sous lesquelles s'exprime la variabilité empirique. Ce qui permet secondairement, lorsque l'on dispose d'observations empiriques, d'obtenir des informations sur la population dont sont extraites les observations.
Passez à la page suivante pour la suite de l'article d'introduction...
1.1. La Statistique et les statistiques

L'emploi très courant du substantif les statistiques dans le français journalistique fait que l'on a parfois tendance à oublier qu'à côté des données numériques couramment utilisées dans la vie sociale, existe la statistique, une science dont l'objet est précisément de déterminer les conditions de production de ces données numériques. Selon le Grand Robert Électronique, la Statistique est une
Étude méthodique des faits sociaux, par des procédés numériques (classements,dénombrements, inventaires chiffrés, recensements, tableaux…)
On voit immédiatement qu'il ne faut pas confondre la statistique, qui est une discipline scientifique, avec les statistiques qui sont définies par le Grand Robert Électronique, comme un
Ensemble de données numériques concernant une catégorie de faits, et utilisable selon les méthodes de la statistique
Toujours selon le Grand Robert Électronique, le terme «Statistique» vient de l'allemand «Statistik» (1749), qui lui-même dérive du latin moderne « statisticus », relatif à l'État. Ainsi, d'emblée la Statistique avait une visée appliquée.
Nous entendons par statistique la science qui a pour objet de recueillir et de coordonner des faits nombreux dans chaque espèce de manière à obtenir des rapports numériques, sensiblement indépendantsdes anomalies du hasard, et qui dénotent l'existence de causes régulières dont l'action s'est combinée avec celle des causes fortuites.
Théorie des chances et des probabilités,ix, in Lalande, Voc. de la philosophie, art. Statistique.
Autrement dit, la Statistique est une discipline de mathématiques appliquées. Cette application peut être directement dans le champ social ou sociétal, mais aussi dans le champ scientifique, en tant que mode de production et d'évaluation de connaissances.
1.2. Statistique descriptive
Définition
Le premier souci de la démarche scientifique est de décrire la réalité, afin de pouvoir ensuite l'expliquer. L'élaboration des descriptions de la réalité s'appuie toujours sur l'utilisation d'un langage, souvent le langage naturel pour les sciences débutantes. Mais le plus souvent, au fur et à mesure qu'une science progresse, elle se dote d'un langage formel spécifique capable de décrire les concepts qu'elle emploie et leur articulation. Les mathématiques constituent bien sûr un tel langage, mais ce n'est pas le seul. Les chimistes ont créé leur propre langage par exemple. Il peut aussi s'agir de langages informatiques. C'est ainsi que la psychologie scientifique moderne s'appuie de plus en plus sur des descriptions mathématiques ou computationnelles des objets qu'elle se propose d'expliquer.
Lorsque la réalité à décrire porte sur des aspects quantifiables, la statistique descriptive fournit un arsenal conceptuel et des méthodes de calcul appropriées aux descriptions des réalités psychologiques. La statistique descriptive est donc avant tout une méthode permettant de construire des représentations de la réalité sur lesquelles pourront ensuite s'appliquer les opérations mathématiques permettant de manipuler ces représentations. Par exemple, si je m'intéresse au niveau en statistiques d'un groupe d'étudiants de L1, afin de déterminer quel type de cours serait le plus approprié, je peux leur faire passer une épreuve individuelle et calculer ensuite la moyenne générale du groupe. Cette moyenne générale est une statistique descriptive au sens où elle décrit une propriété du groupe d'individus considéré, en l'occurrence le niveau global du groupe.
Nous définirons ici la Statistique descriptive comme
la science de la représentation de la réalité empirique au moyen de nombres, ainsi que les méthodes engendrées par cette science.
Dans ce cours, nous considérerons plusieurs façons de représenter numériquement la réalité, ainsi que différentes façons de construire des représentations graphiques pertinentes.
Remarque importante : nous définissons ici la Statistique descriptive comme une science... ET comme un ensemble de méthodes. Cela risque de choquer les statisticiens chercheurs pour qui il s'agit véritablement d'une science. Mais notre propos est plus modeste que celui de contribuer à une science. Nous n'entendons pas enseigner la statistique descriptive en tant que science, mais en tant méthode. Nous nous limitons donc à chercher à en faire comprendre l'utilisation par ses utilisateurs potentiels, à savoir les étudiants en sciences humaines. À cette fin, il est plus utile d'envisager la statistique descriptive comme un art, au même titre que la médecine ou la psychologie du praticien sont des arts, alors que la médecine ou la psychologie du chercheur sont des sciences. Les chercheurs développent les connaissances générales du domaine, la science proprement dite, alors que les seconds confrontent les connaissances générales produites par les premiers à la réalité empirique, à des cas concrets qui se laissent plus ou moins facilement réduire aux inévitables simplifications du réel que représente la science.
Mais... à quoi cela sert-il ?
Pour un humain, il est utile de se représenter la réalité. En effet, cette représentation lui permet d'anticiper dans une certaine mesure le comportement de la réalité, ainsi que les transformations de la réalité qui seront induites par les actions physiques sur cette réalité. La représentation statistique vise exactement les mêmes buts car elle n'est que l'une des nombreuses formes de représentation possibles du réel.
Alors pourquoi s'embêter à passer par des nombres qui sont, c'est le moins qu'on puisse dire, assez peu intuitifs pour le commun des mortels ? Pour une raison très simple : les nombres ont des propriétés combinatoires connues de sorte qu'une fois la réalité exprimée avec des nombres, les transformations mathématiques que j'appliquerai sur cette représentation devraient continuer à traduire la réalité empirique que je cherche à décrire. Par exemple, si je mets quatre pommes dans un sac vide, et qu'ensuite je me retrouve avec 7 amis, je sais directement, sans manipuler physiquement les pommes, qu'il me faudra couper toutes les pommes en deux pour donner à chacun la même quantité. Je le sais parce que 4 divisé par 8 = 1/2 et que je sais que pour obtenir une demi-pomme, il suffit de la couper en deux. Certaines opérations réalisées avec les nombres sont très puissantes car elles permettent de décrire de façon simple des réalités très complexes, beaucoup trop complexes pour qu'on puisse les gérer mentalement. Par exemple, la psychologie cognitive nous enseigne qu'il est impossible de considérer mentalement plus de quelques élément indépendants à la fois. Or, si mon problème est d'évaluer la santé mentale d'une population, ce sont des millions d'individus qu'il faut pouvoir considérer simultanément. Il n'y a donc aucun espoir de traiter une telle question sans disposer de moyens puissants permettant de résumer les informations recueillies auprès de chacun des individus de la population. C'est justement ce genre de résumés que nous permettent les opérations sur les nombres.
1.3. Statistique inférentielle
Si nous reprenons l'exemple précédent, la note moyenne obtenue nous donne effectivement une description de la réalité recherchée (le niveau réel de la classe) mais il ne s'agit que d'UNE représentation parmi de multiples autres possibles. Tel étudiant peut avoir mal dormi cette nuit là et obtenir une note individuelle plus basse que celle qui correspond à son niveau réel. Tel autre, au contraire, aura eu la chance de tomber sur l'une des rares questions qu'il maîtrisait et ainsi obtenu une note sensiblement supérieure à son niveau réel. Le même test aurait donc pu très facilement donner un résultat descriptif différent. Autrement dit, comme nous l'avons vu plus haut, il existe de la variabilité dans les statistiques descriptives. Il importe donc d'évaluer la qualité des statistiques descriptives obtenues. On peut parler exemple évaluer à quel degré les statistiques descriptives obtenues sont entachées de bruit (c'est-à-dire évaluer la part du hasard dans les données).
Le rôle de la statistique inférentielle est ainsi de fournir une information de second ordre, c'est-à-dire non pas directement une connaissance sur la réalité mais une information sur une représentation de la réalité, celle fournie par les statistiques descriptives.
Ce cours porte exclusivement sur les statistiques descriptives. Nous laissons donc les statistiques inférentielles, qui représentent à elles seules un champ au moins aussi vaste, pour un cours ultérieur.
2. Indices de tendance centrale
Objectifs. Introduire les principales statistiques qui permettent, à partir d'un ensemble d'observations codées dans des variables, de construire un résumé prototypique de l'ensemble des observations, et ce en fonction du type de variables utilisées.
Prérequis. Leçon sur la quantification de la variabilité.
Résumé. L'article présente le mode pour les variables nominales, la médiane pour les variables ordinales, la moyenne pour les variables numériques.

Les trois principaux indices de tendance centrale sont le mode, la médiane et la moyenne. On peut en donner d'autres, mais ce n'est pas le lieu ici. Afin de clarifier l'exposé, on les présentera dans l'ordre de complexité décroissant, qui se trouve correspondre à la familiarité que nous avons avec ces nombres.
2.1. La moyenne
1.1. Généralités
C'est l'indice le plus familier, car nous l'avons rencontré maintes fois à l'école, pour évaluer nos résultats. Considérons une variable numérique, à valeurs continues (ou que l'on peut considérer comme continues compte tenu de la précision de nos instruments de mesure). Par exemple, un industriel veut doser la quantité de sucre à mettre dans une tarte, dans l'idée d'en vendre le plus possible et donc de plaire au plus de gens possible et de déplaire au moins de gens possible. Pour des raisons économiques, il ne pourra pas fabriquer plusieurs sortes de tartes. Imaginons que cet industriel a procédé à un test avec, disons, 200 personnes, et pour chacune de ces personnes, il a déterminé la quantité de sucre optimale, celle qui lui plaît le plus. Le problème est donc de trouver une valeur qui résume l'ensemble des observations de façon à ce que cette valeur minimise les écarts qui existent entre elle et les goûts des différents individus. Autrement dit, on veut la quantité de sucre pas trop grande ni trop petite, un juste milieu en quelque sorte. L'opération mathématique capable d'agréger des mesures individuelles de façon à ce que le résultat minimise la distance avec l'ensemble des observations est la moyenne.
Rappelons simplement ici que la moyenne s'obtient en faisant la somme de chacune des observations puis en divisant par le nombre d'observations. L'étudiant qui le souhaite pourra trouver une description plus détaillée et des tutoriels (pour jamovi, R, et SPSS) dans le rappel de maths consacré à la moyenne.
Géométriquement, calculer la moyenne correspond à trouver le milieu d'un ensemble de points.
Bien que cette procédure soit optimale du point de vue de la minimisation de la distance avec les observations disponibles, il faut cependant être conscient que le résultat obtenu présente un certain nombre de défauts, et qu'il n'est pas toujours possible de le calculer.
1.2. Inconvénient 1 : absence d'existence
Le premier de ces défauts est le fait que le résultat obtenu correspond à un nombre qui ne décrit parfaitement peut-être même pas un seul des individus sur lesquels on a procédé aux observations. Ainsi la chimère du français moyen donne un individu qui mesure exactement 1,75m, a exactement 100 de QI, etc. Cette absence d'existence devient particulièrement flagrante si l'on considère non plus des nombres continus mais des nombres entiers. On peut parfaitement calculer qu'une femme française a 1,9 enfants. Pour le premier enfant, on voit, mais à quoi peut bien ressembler le 0,9 enfant restant ? Même s'il peut-être utile à bien des égards, ce nombre est donc une chimère algébrique, mais pas une réalité physique. En même temps, c'est tout de même informatif et permet de voir que nous sommes plus proches en France du seuil de renouvellement de la population (2,1 enfants par femme, que, disons, l'Italie).
1.2. Inconvénient 2 : sensibilité aux valeurs extrêmes
Le deuxième inconvénient de la moyenne est que cet indice est très sensible aux valeurs extrêmes, c'est-à-dire que les observations qui sont très différentes de reste de l'ensemble des observations pèsent plus lourd dans le calcul de moyenne que les autres observations. Ainsi, si nous calculons la moyenne des revenus en France, les 1% de revenus les plus hauts vont peser un poids démesuré par leur caractère complètement hors de proportion avec le salaire des autres individus de la société. Et plus la société sera inégalitaire, plus le calcul du revenu moyen sera biaisé par les hauts revenus. Autrement dit, si l'on mesure la moyenne en enlevant les 1% de revenus les plus hauts, le résultat sera très différent de celui qu'on obtiendrait en incluant ces individus. Mais surtout, ce sera dans des proportions plus importantes que ce qu'on obtiendrait en retirant n'importe quel autre individu. Et finalement le résultat sera alors beaucoup plus représentatif de la réalité de la pyramide des revenus.
2.2. La médiane et le mode
A. La médiane
A.1. Intérêt de la médiane
Considérons une variable ordinale. Il s'agit, rappelons-le, une variable dont les modalités (ou les valeurs, lorsqu'il s'agit d'une variable continue) sont ordonnées les unes par rapport aux autres. C'est le cas par exemple des rangs d'arrivée dans une course (1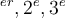 et
et 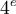 ex-aequo, etc.). Il est clair que cela n'a aucun sens d'additionner ces nombres : ici 1+2 n'est pas égal à 3. 1+2 ne veut simplement rien dire. Comme la moyenne est avant tout une somme pondérée par le nombre d'observations, il n'a donc aucun sens de calculer une moyenne avec de tels nombres. Nous devons donc nous donner un autre indicateur de centralité que la moyenne.
ex-aequo, etc.). Il est clair que cela n'a aucun sens d'additionner ces nombres : ici 1+2 n'est pas égal à 3. 1+2 ne veut simplement rien dire. Comme la moyenne est avant tout une somme pondérée par le nombre d'observations, il n'a donc aucun sens de calculer une moyenne avec de tels nombres. Nous devons donc nous donner un autre indicateur de centralité que la moyenne.
L'indicateur de centralité privilégié pour les données ordinales est la médiane.
En effet, puisqu'une relation d'ordre traduit une disposition des observations entre elles, l'indice de centralité traduit le centre d'un classement : c'est le point tel que la moitié des observations sont plus grandes et l'autre moitié des observations sont plus petites. En fait, le détail du calcul est un peu plus compliqué que cela, car il faut tenir compte du nombre d'observations dans la série, et aussi de la possibilité de l'existence d'ex aequo.
Contrairement à la moyenne qui se définit par une formule, la médiane se définit difficilement par une formule, car son calcul suppose de procéder préalablement à un rangement des données : il faut commencer par ordonner les observations de la plus petite valeur à la plus grande (ou l'inverse). Si nous sommes dans le cas simple où le nombre d'observations est impair et où il n'y a pas d'ex aequo, la médiane est tout simplement la valeur de l'observation du milieu, puisque la moitié moins 1 des observations seront plus grandes et la moitié moins 1 des observations seront plus petites.
A.2. Avantages et inconvénients de la médianeOn l'aura compris, le premier avantage de la médiane est de ne pas nécessiter plus de propriétés qu'une simple relation d'ordre entre les nombres. Du coup, on peut l'utiliser même si la somme n'a aucun sens.
Le deuxième avantage est que la médiane n'est pas sensible aux valeurs extrêmes.
Par exemple, prenons la série de trois observations suivantes : 2; 5; 20.
La moyenne est 27 / 3 = 9. La médiane est 5.
Imaginons que, suite à un problème, la troisième valeur soit 500. La moyenne devient 169 tandis que la médiane reste à 5. On voit donc que la médiane n'est tout simplement pas sensible au niveau d'éloignement des valeurs, seulement à leur rang.
L'inconvénient évidemment, c'est que si l'éloignement extrême de la valeur était justifié, cette absence de prise en compte constitue une perte de sensibilité par rapport à la moyenne.
L'étudiant qui le souhaite pourra trouver sur ce site des tutoriels pour calculer des médianes en cochant simplement la case appropriée dans un logiciel de statistiques (ici jamovi ou R). Le calcul de la médiane par tableur se réalise exactement comme pour calculer des moyennes, mais en utilisant la fonction MEDIANE au lieu de MOYENNE.
B. Le mode
Lorsque la variable étudiée ne possède même pas les propriétés d'une variable ordinale, c'est-à-dire lorsque ses modalités doivent simplement être considérées comme des catégories mutuellement exclusives sans qu'une relation d'ordre les relie, une seule opération est possible : compter simplement combien d'observations se trouvent dans chacune des modalités de la variable.
Dans ce cas, la tendance centrale revient simplement à la modalité qui possède le plus d'observations : c'est ce qu'on appelle le « mode de la variable ». La procédure de calcul d'un mode : on compte le nombre d'observations par modalités de la variable est le mode est la valeur de la modalité la plus fréquente.
Clairement, cet indice est assez pauvre, mais c'est le seul disponible lorsque la variable est nominale. Par contre, si vous rapportez un mode, en tant que valeur de la modalité dominante, pensez à rapporter en même temps le pourcentage d'observations qui se sont concentrées sur le mode. Ainsi, on obtient une information supplémentaire sur le degré de dominance de ce mode.
Dire que le mode peut être plus ou moins dominant, c'est remarquer que les données sont plus ou moins dispersées dans les différentes modalités. Cela nous mène à l'article suivant, qui concerne les indices permettant d'évaluer la dispersion des données.
3. Indices de dispersion
Objectifs. L'objet de cet article est de fournir un ensemble d'indices calculables à partir d'un échantillon de données afin de traduire à quel point les données de cet échantillon sont dispersées ou au contraire à quel point elles se laissent bien résumer par une valeur centrale.
Prérequis. Leçon sur les indices de tendance centrale.
Résumé. L'article présente l'écart-type et l'erreur-standard pour les variables numériques, l'écart inter-quartiles pour les variables ordinales. Les avantages et inconvénients des différents indices de dispersion sont présentés.

Comme les indices de tendance centrale, les indices de dispersion utilisables dépendent du type de variables concernées. Il y a toutefois plusieurs types d'indices de dispersion possible pour chaque type de variable. Selon le type de données à résumer (nominale, ordinale, numérique) on pourra utiliser des indices appropriés. En allant des données les plus complètes (numériques) aux plus frustes, on pourra utiliser les indices suivants :
- Indice numérique : la variance et l'écart-type
- Écarts-interquartiles
- Entropie
Nous adopterons ici le type de variable comme point d'entrée dans le plan. Comme pour l'article précédent, nous partirons des variables numériques, les plus familières, et nous descendrons progressivement dans les propriétés disponibles.
3.1. Dispersion des variables numériques
A. Min, Max et Étendue
L'étendue, ou intervalle de variation, est la plus simple des mesures de dispersion que l'on peut obtenir avec des variables numériques. Il s'agit tout simplement de la différence entre la valeur la plus forte et la valeur la plus faible. Si l'on a une variable numérique X, et que l'on note Max(X) la valeur la plus forte et Min(X) la valeur la plus faible, on a donc :
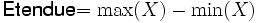
Pour information, le min et le max d'une série de données sont directement accessibles comme des fonctions de tableur, au même titre que la somme ou la moyenne.
Dans le cas de variables numériques, l'interprétation naturelle de l'étendue est une distance : la distance maximale qui sépare deux données de l'échantillon.
Lorsque l'on travaille avec des données empiriques, éventuellement issues d'un recodage, il est important de regarder les valeurs Min et Max, car c'est un moyen simple de détecter des erreurs de saisie. Si vous avez une échelle de mesure qui permet d'avoir des notes de 0 à 10 par exemple, et que le max dépasse 10, c'est nécessairement qu'une erreur de saisie a été commise. Ce type d'erreur est très fréquent, et presque inévitable lorsque les données sont nombreuses et que leur saisie n'est pas réalisée par l'intermédiaire d'un programme informatique capable de les détecter au moment même de la saisie. Or une seule erreur de ce type peut changer très sensiblement les calculs de moyenne ainsi que les calculs des variables de dispersion que nous allons voir maintenant.
Parfois, certaines valeurs sont ainsi très différentes des autres, sans correspondre à des erreurs de saisie ou de logiciel. On parle de valeurs aberrantes (en anglais «outliers»). Par exemple, on enregistre des temps de réponse sur une tâche à laquelle les sujets mettent en général 2 à 3 secondes à répondre. Et on observe que pour certaines observations, le temps dépasse une minute. Il est donc très probable que quelque chose d'anormal s'est passé au moment du recueil pour ces sujets.
B. Variance et écart-type
Variance et écart-type d'une population
La variance représente une dispersion. L'idée de base est que la dispersion s'évalue à partir d'une valeur centrale : plus les observations sont loin de la valeur centrale, et plus elles sont dispersées. Puisqu'on est dans un cas où la variable est numérique, la valeur centrale que l'on pourra prendre sera naturellement la moyenne. Une valeur donnée sera donc d'autant plus dispersée qu'elle sera loin de la moyenne
 . En première approximation, il pourrait donc suffire de calculer la moyenne des écarts à la moyenne pour avoir une évaluation de la dispersion des données de l'échantillon. Pour une raison que nous détaillerons ensuite, on préfère cependant calculer la moyenne des carrés des écarts à la moyenne.
. En première approximation, il pourrait donc suffire de calculer la moyenne des écarts à la moyenne pour avoir une évaluation de la dispersion des données de l'échantillon. Pour une raison que nous détaillerons ensuite, on préfère cependant calculer la moyenne des carrés des écarts à la moyenne.
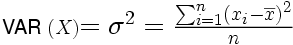
et l'écart-type de la population pourra alors aussi être calculé comme la racine carrée de la variance, soit
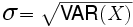
Pourquoi prend-on la somme des carrés des écarts, et pas les écarts eux-mêmes ?
Pour répondre à cette question, imaginons que nous ayons deux mesures, une qui représente la moyenne +1 et l'autre qui représente la moyenne-1. Par exemple, sur la figure ci-dessous, la moyenne est m et la dispersion de ces deux mesures est représentée par l'accolade qui relie m -1 et m +1.
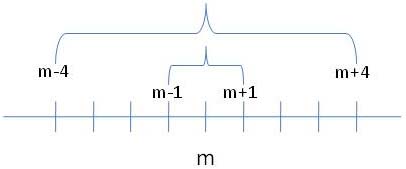
Si je fais la somme des écarts de ces deux données à la moyenne, j'obtiendrai 1-1 = 0. Imaginons maintenant que nous ayons deux autres mesures, une qui représente la moyenne +4 et l'autre qui représente la moyenne -4. Si je fais la somme des écarts à la moyenne de ces deux nouvelles données, j'obtiendrai 4-4 = 0. L'indice obtenu en sommant les écarts à la moyenne n'est donc pas capable de reconnaître que le deuxième couple de données est plus dispersé autour de la moyenne que le premier, chose que l'intuition nous indique pourtant sans effort : il suffit de voir sur le schéma ci-dessus que les deux accolades n'ont pas la même largeur.
L'avantage de sommer les carrés des écarts plutôt que les écarts eux-mêmes tient à ce que les écarts positifs et négatifs ne s'annulent alors plus. ET de ce fait, le carré moyen des écarts du premier couple de données est de 1+1 = 2, divisé par 2, soit 1. Pour le second couple de données, le carré moyen des écarts est 16+16=32... Cette fois, on voit clairement que le second couple est plus dispersé autour de la moyenne que le premier.
Variance d'un échantillon
Bien souvent, en recherche, on ne s'intéresse pas seulement à décrire les caractéristiques d'un échantillon, mais on cherche à se faire une idée des caractéristiques de la population dont l'échantillon est issu. Si on a pris soin de choisir un échantillon bien représentatif de la population cible, celle au sujet de laquelle on veut apprendre quelque chose, alors la moyenne de l'échantillon nous renseigne sur la moyenne de la population, et l'estimation de la taille des écarts nous renseigne sur la dispersion des mesures qu'on aurait dans l'ensemble de la population. On peut montrer qu'une bonne estimation de la variance de la population est obtenue à partir de l'échantillon en divisant la somme des carrés des écarts à la moyenne par n-1 au lieu de n.
Définition. Soit un échantillon de n données mesurées sur une variable X, où Xi représente la ième donnée de la variable X. La variance de cet échantillon est donnée par :
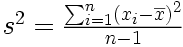
où
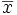 dénote la valeur moyenne de
X.
dénote la valeur moyenne de
X.
Écart-type d'un échantillon
En travaillant avec les carrés, nous avons évité un problème. Toutefois, le résultat obtenu n'est plus dans la même métrique que la valeur qu'on a cherché à mesurer. Par exemple, si on a mesuré des longueurs, la variance traduit bien la dispersion des données de l'échantillon mesures, mais puisqu'on a moyenné des mètres carrés et non des mètres, le résultat n'est pas directement interprétable en termes de la variable cible !
Pour avoir un indice de dispersion qui soit dans la même unité que la variable cible, on est donc conduits à utiliser la racine carrée de la variance et non la variance elle-même : c'est l'écart-type, noté directement s .
C. Variance d'erreur et erreur standard (aussi appelée erreur-type)
Lorsque l'on procède à une expérience, on travaille à partir d'un échantillon et non à partir de la population entière. Si l'on recommence l'expérience avec un autre échantillon, on aura un résultat légèrement différent. Le simple fait de travailler avec un échantillon aléatoire plutôt qu'avec l'ensemble de la population induit une erreur. Une partie de la dispersion totale des mesures est donc due à l'échantillonnage. Si l'on exprime la variabilité par la variance, on dira donc qu'une partie de la variance totale est de la variance d'erreur.
Logiquement, la part de cette variance d'erreur est d'autant plus faible que l'échantillon est grand. Cela a pour conséquence que si l'on veut comparer des dispersions provenant d'échantillons de tailles différentes, ces derniers présenteront des niveaux de biais différents. Par exemple, supposons que l'on compare quatre groupes de sujets. Supposons encore que l'un des groupes soit sensiblement plus petit que les trois autres. En ce cas, la comparaison des dispersions dans ces différents groupes n'est pas possible, sauf à disposer d'une mesure de dispersion moins biaisée par la taille de l'échantillon. Cette mesure, c'est l'erreur standard que l'on obtient en divisant la variance par la racine carrée de l'effectif.
On pourra alors avoir deux cas selon que l'on considère la population ou l'échantillon.
Cas de la population :
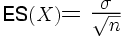
Cas de l'échantillon :
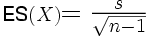
D. Écart absolu moyen (aussi appelé déviation moyenne)
Si vous êtes plus tard amenés à lire certains articles de recherche, vous risquez de rencontrer un autre type de mesure de dispersion que l'on utilise parfois, à savoir la déviation moyenne. La logique est la même que celle de la variance, sauf qu'au lieu d'élever les écarts à la moyenne au carré pour s'affranchir du problème des écarts négatifs qui s'annulent avec les écarts positifs, on ramène tous les écarts à des valeurs absolues avant de les moyenner. Ce qui donne la formule suivante :
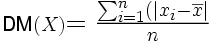
3.2. Dispersion des variables ordinales
Nous allons retrouver ici la notion d'étendue, vue dans le cas des variables numériques. Toutefois, interpréter une étendue comme une distance n'aurait aucun sens. Lorsque les variables sont ordinales, il ne sert à rien de calculer des sommes et des différences comme on le fait dans les calculs vus précédemment. Par contre, on peut utiliser la relation d'ordre. Autrement dit, on va commencer par ranger les observations de la plus petite à la plus grande (ou l'inverse). On peut alors toujours considérer la dispersion comme une étendue, mais en interprétant cette dernière sous l'angle des valeurs qui permettent de repérer une certaine proportion d'observations.
A. Notion de quantiles
De façon abstraite, si nous avons un échantillon de n observations, nous pouvons le partager en k parties de même effectif. Dans le cas général, on appelle chacun des groupes ainsi obtenus un quantile. Certains quantiles ont des noms particuliers. La médiane est la valeur qui partage l'échantillon en k =2 quantiles, dont le nom est bien connu : ce sont des moitiés.
Par exemple, imaginons que nos observations soient la série des 12 premiers entiers naturels positifs, de 1 à 12. Nos données d'entrées sont donc :
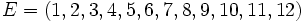 .
.
La première moitié contient les
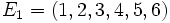 .
.
et la seconde moitié
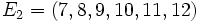
La médiane correspond à une valeur qui partage ces observations en deux moitiés. Nous prendrons donc naturellement 6,5. On voit aisément que tous les éléments de E 1 sont bien inférieurs à 6,5 tandis que tous ceux de E 2 sont supérieurs.
Si
k
=100, nous appellerons
centile
des groupes ordonnés d'observations tels que chaque groupe contient 1% des observations. Les
percentiles
correspondent aux valeurs qui bornent les centiles et non aux intervalles eux-mêmes. Ainsi le 50 percentile est la médiane.
percentile est la médiane.
si k =10, nous appellerons décile, des groupes ordonnés d'observations tels que chaque groupe contient 10% des observations. Le premier décile contient donc les 10% d'observations les plus basses. Le deuxième décile contient 10% d'observations qui sont toutes plus grandes que les valeurs du premier décile (ou égales à la plus grande de ces valeurs en cas d'ex æquo), et qui sont toutes plus petites que les valeurs du troisième décile (ou égales à la plus petite de ces dernières valeurs en cas d'ex æquo).
Munis de cette notion de quantile, nous pouvons exprimer des indices de dispersion ordinaux, qui correspondent alors à des étendues réduites d'un certain nombre des quantiles les plus extrêmes.
B. Quartiles et écarts inter-quartiles
En reprenant la notion de quantile, et si k =4, nous avons 4 quartiles qui correspondent chacun à 1/4 = 25% des observations. Les quantiles qui représentent 1/4 des observations s'appellent des quartiles. Un échantillon possède donc 4 quartiles.
On appelle aussi quartiles, les trois valeurs qui partagent l'échantillon en 4. Dans cette acception, le premier quartile est la valeur Q1 qui partage le premier et le deuxième ensemble de 25% d'observations. Le deuxième quartile, Q2, est la médiane. Le troisième quartile, Q3, est la valeur qui partage le troisième et le quatrième ensembles de 25% d'observations.
On appelle alors Écart interquartile l'étendue comprise entre le troisième et le premier quartile. On peut donc le calculer très simplement en faisant la différence de ces deux valeurs.
Si nous reprenons l'exemple de l'ensemble E d'observations vu plus haut. Le premier quartile contient les 25% d'observations les plus basses soit
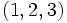
Les quartiles suivants contiennent les 25% d'observations suivantes
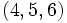
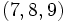
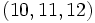
En tant que valeurs, les trois quartiles sont Q1 = 3,75, Q2 = 6,5 qui est par ailleurs la médiane, et Q3 = 9,25.
L'écart interquartile est alors simplement la différence entre Q3 - Q1, soit ici 9,25-3,75 = 5,5.
Si nous l'interprétons en termes d'étendue, l'écart interquartile correspond à un ensemble de valeurs autour de la médiane tel qu'il contient les 50% d'observations les moins extrêmes. Le mode de calcul de l'espace interquartile n'est d'ailleurs qu'un cas particulier d'opération utilisant des distributions tronquées, c'est-à-dire de distribution dont on a retiré les valeurs les plus extrêmes.
3.3. Dispersion des variables nominales
Pour des variables nominales, la seule relation qui existe entre les modalités est l'exclusivité mutuelle, à savoir que si une observation tombe dans une modalité, elle ne tombe pas en même temps dans une autre. Si un sujet possède la modalité Homme sur la variable Sexe, il ne possède pas la modalité Femme.
Ceci étant posé, il ne reste pas beaucoup de possibilités pour évaluer la dispersion des données. On peut simplement travailler sur les fréquences d'observations qui tombent dans chaque modalité. La quantité utilisée pour quantifier la dispersion avec des variables nominales s'appelle l'entropie, mais son utilisation dépasse le niveau d'un cours de statistiques de L1 en sciences humaines, aussi ne la verrons-nous pas plus avant pour le moment. Pour le moment, il suffit de retenir les principes suivants :
1°) plus il y a de modalités à effectif non nul, et plus la dispersion est grande.
2°) Pour un nombre de modalités possibles donné, la dispersion est maximale, si les observations sont également distribuées dans toutes les modalités. Elle est minimale si toutes les observations sont regroupées dans une seule modalité.
4. Représentations graphique des distributions
Objectifs. Introduire la notion de représentation graphique d'une distribution et la distinction entre représentation théorique et représentation à partir d'échantillons.
Prérequis. Les différents articles de la grande leçon Psychologie, statistique et psychométrie, et en particulier l'article de généralités sur les distributions statistiques. Essentiel sur les histogrammes.
Résumé. Cet article se propose de développer la notion générale de distribution, sans entrer dans les paramètres mathématiques permettant de caractériser les distributions, mais plutôt en montrant d'abord la construction graphique de ces distributions, puis en présentant différents types de distributions et les éléments qui les engendrent.
4.1. La construction graphique des distributions théoriques
Attention : Pour bien comprendre cette section, il peut être utile de rappeler ce qu'est un histogramme, et savoir comment il est possible d'en construire. Rappelons qu'un histogramme est un mode de représentation graphique qui met en relation une (ou plusieurs) variables discrètes (par exemple des catégories, des classes ordinales, ou des intervalles numériques disjoints) et une variable numérique.
Une distribution est fondamentalement une représentation de la façon dont les observations (théoriques ou empiriques) se distribuent, se répartissent, sur les différentes valeurs d'une variable. Par exemple, imaginons un sociologue qui voudrait examiner les salaires des femmes en France, pour les mettre en relation, par exemple, avec le niveau d'étude. Ne pouvant accéder à l'ensemble des salaires de toutes les femmes travaillant en France, il va se rabattre, comme dans la grande majorité des recherches scientifiques, sur les salaires d'un petit échantillon de femmes. Il va s'arranger pour que cet échantillon ne soit quand même pas trop petit, et surtout qu'il soit représentatif de la population cible, à savoir la population française. Admettons donc qu'il ait bien sélectionné son échantillon, et qu'il se trouve à la tête d'un ensemble de, disons, 1000 salaires de femmes. Admettons aussi qu'il a vérifié que ses données ne contiennent pas déjà d'erreur de recueil ou de saisie. Que faire ensuite ?
La première chose à faire, c'est précisément de regarder la forme de la distribution des salaires dans son échantillon. Mais pour étudier cela, il nous faut faire un détour par un rappel un peu conceptuel de ce qu'est une distribution.
Dans le cas général, une distribution statistique théorique décrit la probabilité de trouver une valeur dans un échantillon : la surface sous la courbe représente une proportion d'observations. Par exemple, la courbe suivante décrit une distribution « normale ». On remarque que la probabilité (techniquement, on parle plutôt de « densité de probabilité ») d'avoir une observation autour de zéro est la plus forte et qu'elle décroît d'autant plus qu'on s'éloigne du zéro. Elle devient quasiment nulle très rapidement.
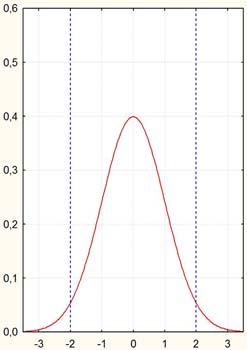
Sur la courbe de la page précédente, on voit aisément qu'il s'agit là d'une représentation graphique théorique. Par exemple, les valeurs sur les axes sont continues. Mathématiquement, cela veut dire qu'entre deux nombres, aussi rapprochés soient-ils, on peut toujours en insérer une infinité d'autres. Or dans un échantillon réel, avec des données observées donc, on ne dispose pas d'une infinité d'observations, mais toujours d'un nombre (très) limité. On ne sait donc généralement rien de la proportion d'observations qui tombent en un point donné. Il existe une infinité de points pour lesquels on ne dispose d'aucune observation, et un tout petit nombre de points pour lesquels on en a, le plus souvent, une seule. Si l'on traçait un tel graphique, on aurait quelque chose d'illisible. Dans ces conditions, comment faire ?
Il faut distinguer deux cas, selon que la variable que l'on étudie possède des valeurs discrètes ou continues. Commençons par le cas discret.
4.2. Distributions observées, cas discret
2.1. Histogrammes
Si les valeurs sont discrètes, la solution est immédiate : il suffit de tracer un histogramme en prenant les modalités de la variable pour l'axe des X, et l'effectif dans chaque modalité sur l'axe des Y, et le tour est joué. Rappelons qu'un histogramme est un mode de représentation graphique qui met en relation une (ou plusieurs) variables discrètes (par exemple des catégories, des classes ordinales, ou des intervalles numériques disjoints) et une variable numérique. En voici un exemple :
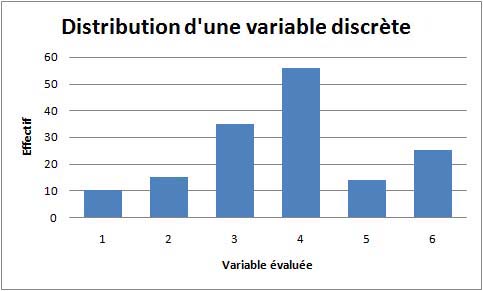
Bien que claire, la représentation précédente présente une particularité, qui pourra s'avérer importante selon l'usage qui est visé pour la représentation de la distribution. S'il s'agit de comparer deux distributions ayant le même effectif et le même nombre de modalités, et si l'on a pris soin de garder la même échelle pour l'axe des Y, alors pas de problèmes, les deux graphiques seront directement comparables. Mais si les deux distributions à comparer ont des effectifs très différents (par exemple, on veut comparer la distribution obtenue sur l'ensemble de la population française avec ce qui a été obtenu sur un échantillon donné représentant, disons, 60000 fois moins d'observations), la comparaison directe ne sera plus possible. Il sera alors plus avantageux de remplacer les effectifs bruts dans chaque modalité par le pourcentage d'observations qui tombent dans chaque modalité. Ainsi les deux histogrammes deviennent comparables. Par exemple :
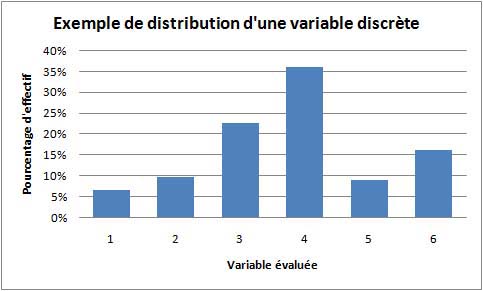
Sur cet exemple, on voit bien que la forme n'a pas changé, mais l'axe des Y est maintenant exprimé avec des pourcentages et deux distributions d'effectifs bruts très différents deviendraient comparables.
2.2. Les boîtes à moustaches (ou «Boxplots»)
Les boîtes à moustaches sont une représentation de la distribution d'une variable qui repose sur cinq valeurs. Le rectangle central représente le gros de la distribution, avec la valeur centrale, généralement la médiane, marquée ici par une ligne. Les petits traits placés aux extrémités indiquent les bornes extérieures de la distribution. Toutefois, selon le paramétrage du logiciel, ces valeurs peuvent correspondre à des fonctions différentes.
Dans ce premier exemple, où est représentée une distribution des trois notes sur 20 obtenues par 500 étudiants à un concours écrit d'entrée dans une grande école, avec une épreuve de maths, une épreuve de physique et une épreuve d'anglais, on a une boîte à moustache par note. Les cinq valeurs considérées sont le Min et le Max pour les extrémités, et les trois quartiles pour le rectangle central. Les quartiles Q1 et Q3 délimitent le rectangle central qui, de ce fait, représente directement l'écart interquartile. La médiane (= quartile Q2) est la ligne interne au rectangle. Les points vers les extrémités représentent des valeurs extrêmes, c'est-à-dire des notes qui se démarquent sensiblement des notes obtenues par le reste des candidats.
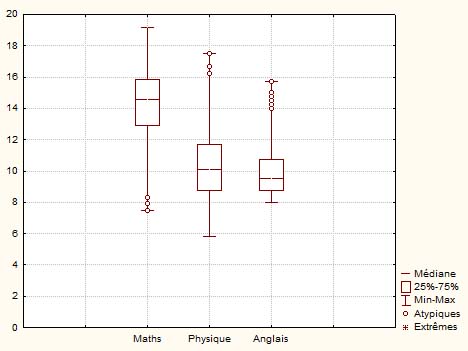
Dans ce second exemple, les trois mêmes distributions sont représentées par des boîtes à moustaches mais les valeurs extrêmes sont maintenant les valeurs considérées comme correspondant à l'étendue des valeurs non-atypiques. De ce fait, les valeurs extrêmes marquées par les petits cercles se retrouvent en dehors de cette étendue.
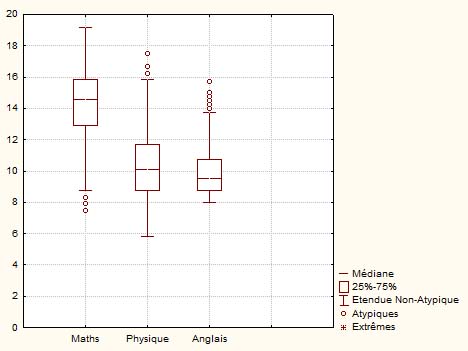
Nous terminerons par un troisième exemple dans lequel les valeurs marquant les extrémités des moustaches sont définies par le premier et le 99ème percentile. Autrement dit, les notes telles que 1% des notes sont plus petites que la moustache basse, et 1% des notes sont plus hautes que la moustache haute.
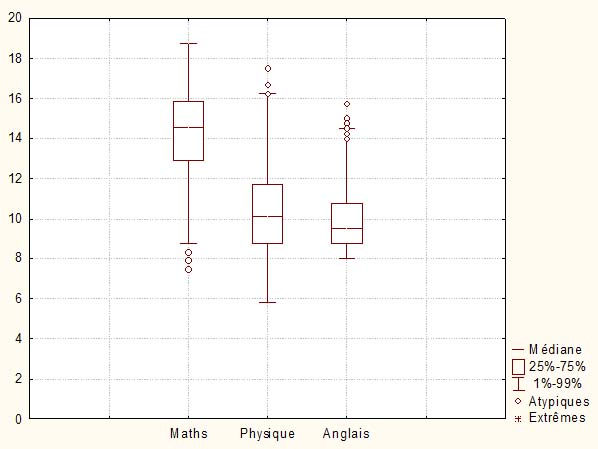
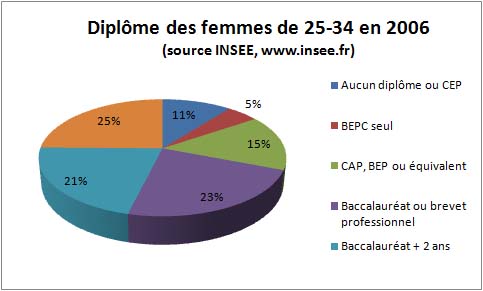
2.3. Diagrammes à secteurs "Camemberts"
Lorsqu'il s'agit de représenter les effectifs par modalités d'une variable discrète, une représentation très commune est le diagramme à secteurs ou « camembert », par analogie évidente avec la forme usuelle de la boîte du fromage éponyme.
Voici un exemple :
4.3. Distributions observées, cas continu
Tout d'abord, commençons par remarquer que parler de valeurs continues pour des données d'observations est en réalité un abus de langage. En effet, mathématiquement une variable est continue si quelles que soient deux valeurs de cette variable, on peut toujours avoir une troisième valeur qui vient s'intercaler entre elles. Par exemple, entre 2,3 et 2,4 on peut placer 2,35. Entre 0,000000001 et p 0,000000002, on peut placer p 0,0000000015. Et ainsi de suite à l'infini. Parler de valeurs continues pour une variable observée signifie donc que l'on serait capable de discriminer entre deux valeurs infiniment proches.p Mais absolument p aucun instrument de mesure ne dispose d'une précision infinie. Donc quand on parle de valeurs observées sur une dimension continue, en réalité, on dit simplement que notre dispositif de mesure permet suffisamment de finesse pour nous donner l'impression de continuité. p Un peu de la même façon que les pixels sur un écran d'ordinateur sont suffisamment proches les uns des autres pour nous donner l'illusion de continuité de l'image alors qu'en réalité les pixels sont bien séparés les uns des autres. Ou encore comme lorsque au cinéma, nous avons l'impression d'un mouvement fluide et continu alors qu'il ne s'agit que d'une série rapidement diffusée d'images nettement séparées. Toutes les données d'observation ne sont en réalité que fictivement continues, même en supposant que la variable théorique qu'elles sont censées mesurer soit, elle, continue. p
Une fois admis ce principe, on est fondé à utiliser la technique de l'histogramme pour représenter n'importe quelle distribution, que la variable observée soit discrète ou pseudo-continue.
La solution technique pour construire l'histogramme consiste à découper l'axe des p X p en intervalles, et à regrouper pour les compter ensemble toutes les observations qui tombent dans cet intervalle. On va ainsi obtenir un tableau avec, pour chaque valeur, le nombre d'observations associées. À partir de là, il ne restera plus qu'à tracer l'histogramme correspondant. Cet histogramme sera alors la représentation graphique de l'échantillon. Et dans la mesure où l'échantillon est la meilleure estimation de la population cible, il constitue par là même une représentation de la distribution de la population cible. Ce n'est évidemment pas la seule possible. Il suffit d'avoir un autre échantillon, plus large et/ou plus représentatif de la population cible pour pouvoir en extraire une meilleure représentation de la distribution cible.p
Dans l'exemple de la figure qui suit, les valeurs portées sur l'axe des axes sont liées à une variable calculée, et le mode de calcul fait que cette variable était donné avec 7 décimales après la virgule. Nous avons donc là une précision des données exagérées (ne correspondant pas à la vérité de ce que nous étions capables de mesurer effectivement), et en tout cas suffisamment élevée pour que cela représente un nombre de modalités considérable, largement supérieur au nombre d'observations disponibles. Nous sommes donc dans un cas où il faut construire des intervalles permettant d'agréger les observations. Ici, il a été demandé au logiciel de construire 13 intervalles. Le logiciel de statistiques a donc découpé l'étendue des observations (i.e., la différence entre la plus grande et la plus petite valeur) entre 13 intervalles de taille égale, et a compté combien d'observations tombaient dans chacun des 13 intervalles. La courbe en rouge a été ajoutée par le logiciel pour indiquer ce que serait la distribution théorique si ces données correspondaient à une distribution normale. On peut donc avoir une impression visuelle de la normalité (ou non) des données issues de l'échantillon.p
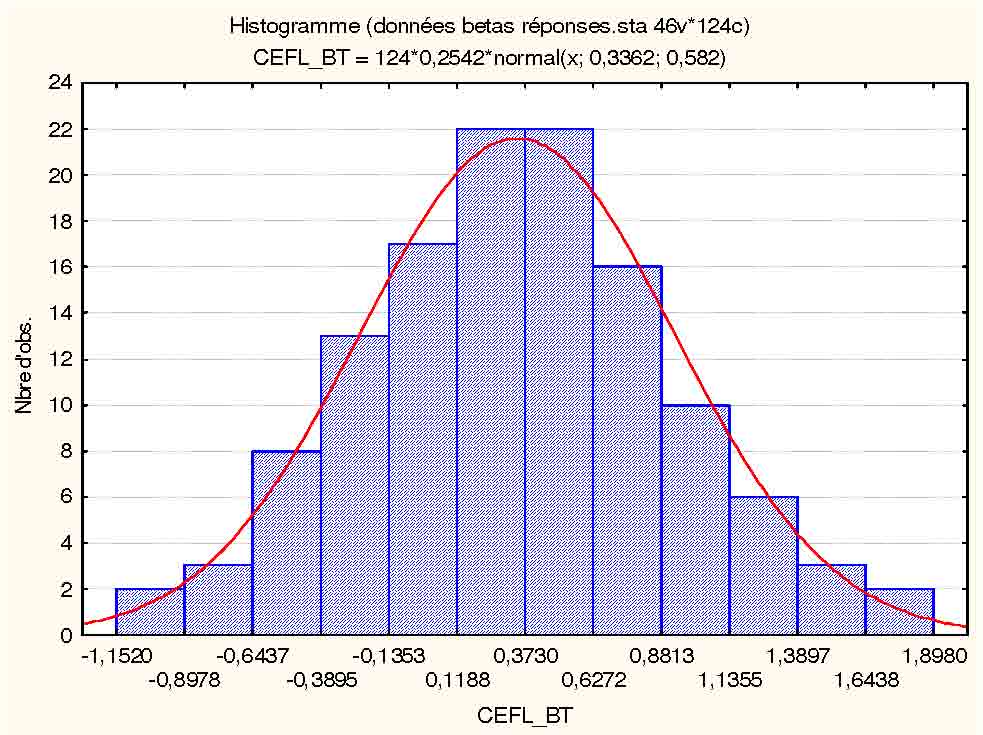
Remarquons que la taille des intervalles peut varier, puisqu'elle dépend du nombre d'intervalles qu'on choisit de prendre. C'est un choix de la part de la personne qui construit la représentation. On remarquera alors que selon le choix de la taille des intervalles, la distribution peut parfois changer de forme. Au minimum, on prendra des intervalles correspondant à la précision de notre dispositif de mesure puisque de toute façon, des intervalles plus fins n'auraient aucun sens. En revanche, on peut être amené à faire des regroupements plus larges. En effet, p toutes choses égales par ailleurs, plus l'on prend des intervalles fins et plus le nombre d'observations dans chaque intervalle sera petit. À la limite, on risque de retomber sur le problème qu'on aurait avec de vraies variables continues, à savoir une seule observation dans quelques intervalles et aucune observation dans la plupart des intervalles. Un histogramme quasiment plat en quelque sorte, donc très peu informatif. Une solution naturelle consiste alors à choisir des intervalles plus larges, donc moins nombreux, mais contenant plus d'observations. Il n'y a pas de règle de choix stricte. Le choix de la bonne taille d'intervalles est affaire d'intuition du chercheur, en fonction de ce qu'il veut montrer et en fonction des propriétés des données dont il dispose.
5. Quelques distributions statistiques remarquables
Objectifs. Au plan conceptuel, faire comprendre pourquoi il existe des distributions différentes, et introduire quelques distributions importantes.
Prérequis. Les différents articles de la grande leçon Psychologie, statistique et psychométrie, et en particulier l'article de généralités sur les distributions statistiques. Essentiel sur les histogrammes.
Résumé. Cet article se propose de développer la notion générale de distribution, sans entrer vraiment dans les paramètres mathématiques permettant de caractériser les distributions, mais plutôt en présentant la logique qui préside à la construction des différents types de distributions.
5.1. La distribution uniforme (rectangulaire)
Imaginons que l'on compte sur une année combien d'individus naissent chaque jour de la semaine en France. On obtient donc un nombre pour les lundis, un pour les mardis, etc. Si l'on divise ces nombres par le nombre total de naissances annuelles, on obtient ainsi pour chaque jour la probabilité qu'un individu pris au hasard naisse un lundi, un mardi, etc. Approximativement, cette probabilité sera la même pour chacun des jours de la semaine. Autrement dit la courbe obtenue ressemblera à un rectangle. C'est une distribution rectangulaire.
Bien entendu, si l'on prend un dé non pipé et qu'on regarde la probabilité que chacune des six faces sorte, on obtiendra aussi une distribution rectangulaire.
Si, maintenant, on trace le graphe des fréquences de chaque face après avoir lancé un grand nombre de fois un dé (grand échantillon), on devrait observer quelque chose qui ressemble à un rectangle, faute de quoi il sera plausible que le dé soit en réalité pipé. Voici un exemple de résultats obtenus avec 1015 lancers de dés simulés par ordinateur :
On remarque qu'il y a bien des fluctuations de fréquence d'une face à l'autre, mais celles-ci sont très petites.
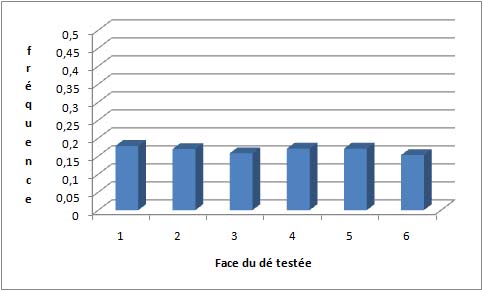
Du point de vue de la représentation graphique, vous pouvez noter que l'on n'a plus ici un axe des X avec des modalités continues, mais discrètes : on a un petit nombre de valeurs bien séparées. Cela provient du fait que nos deux exemples (lancers de dés, nombre de naissances en fonction du jour de la semaine) utilisaient des variables discrètes, c'est-à-dire dont les modalités sont bien séparées. Il n'existe pas de « lundi et demi » dans la semaine ni de « face 4,3 » sur un dé. Cela n'aurait donc aucun sens d'utiliser une courbe continue pour représenter la distribution. Il faut cependant bien comprendre que rien n'empêche d'avoir une distribution rectangulaire théorique représentable sur un axe des X à valeurs continues. Par exemple, si on demande à un ordinateur de tirer des milliards de valeurs au hasard entre 0 et 1, de telle façon que chaque point ait la même probabilité de sortir que les autres, on obtiendra une distribution rectangulaire, mais dont les valeurs se répartissent sur un axe à valeurs continues.
5.2. La distribution normale
Si l'on prend un mètre et que l'on mesure la taille d'un enfant, on obtient une valeur. Si l'on refait la mesure, on obtiendra une valeur peut-être identique, mais le plus souvent très légèrement différente. De ce fait, répéter l'opération de mesure permettra de construire une distribution. Depuis au moins Laplace, une question cruciale pour les scientifiques confrontés à l'imprécision et aux petites fluctuations aléatoires des mesures était de comprendre les propriétés mathématiques de cette distribution. En effet, en comparant les propriétés mathématiques d'une distribution donnée aux propriétés mathématique d'une distribution purement due à de petites fluctuations aléatoires, on peut évaluer si la distribution obtenue est biaisée, ou sous l'influence d'un facteur systématique quelconque, ou encore purement explicable par le hasard.
La distribution normale est celle qui traduit la répartition de mesures qui sont entachées d'une somme de multiples petites fluctuations aléatoires, fluctuations qui se produisent inévitablement lorsque l'on mesure une grandeur dans l'univers physique. Cette distribution apparaît dès que certaines conditions très banales sont réunies. L'une de ces conditions est l'existence d'une régression à la moyenne, c'est-à-dire que suite à l'observation de valeurs extrêmes, les valeurs suivantes tendent à revenir vers la moyenne. Il ne s'agit toutefois que d'une tendance et non quelque chose de systématique.
Un exemple de régression à la moyenne est le QI intergénérationnel. La régression à la moyenne en ce cas tient à ce que la moyenne des QI des enfants tend à être 20% plus proche de la moyenne générale de la population (100) que la moyenne des QI des parents. Si le père à un QI de 140 et la mère un QI de 140, leur moyenne fait 140 et le plus probable est que le QI moyen de leurs enfants tourne autour de 132. Il reste bien entendu possible dans certains cas que les enfants de parents dont le QI moyen est 140 aient un QI plus élevé que 132, voire même que 140, mais cela arrivera plus rarement que le contraire. La principale seule raison pour laquelle tout le monde n'a pas exactement 100 au bout de quelques siècles, c'est que la transmission génétique et l'effet de l'environnement où l'enfant grandit possèdent un caractère aléatoire qui fait qu'émergent spontanément des enfants avec des valeurs plus extrêmes que celles de leurs parents. Il reste qu'un très bon prédicteur du QI des enfants est celui des parents, et que ces conditions suffisent à assurer une distribution normale.
Cette distribution théorique est très connue. En voici un exemple :
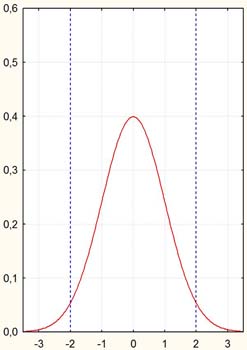
Dans cet exemple, on a représenté une distribution normale de notes dont la moyenne vaut 0 et l'écart-type vaut 1.
Dans la simulation suivante, vous avez la possibilité de faire varier les paramètres de la distribution normale (moyenne et écart-type), puis cliquez sur "Tracez" pour voir directement comment cela affecte la forme de la distribution. À chaque essai, une nouvelle courbe s'ajoutera sur le graphique. Cliquez sur le bouton « Effacez » pour réinitialiser la page. Veuillez noter que l'échelle choisie pour l'axe vertical est plus petite que sur le graphique précédent, ce qui permet de représenter une plus grande diversité de courbes, mais si vous tracez la courbe de moyenne 0 et d'écart-type 1, elle semblera plus aplatie que sur le graphique précédent.
On peut voir sur cette courbe plusieurs propriétés classiques des distributions normales : le pic de fréquence correspond à la note moyenne, la distribution est symétrique autour de cette moyenne, et enfin les valeurs extrêmes correspondent à une raréfaction croissante des observations : plus on s'éloigne de la moyenne, d'une côté comme de l'autre, et plus la fréquence tend vers 0.
Cette distribution s'applique par exemple à la taille des français ou aux notes de QI que l'on peut observer dans une population d'enfants ou d'adultes. Voici quelques propriétés utiles à connaître.
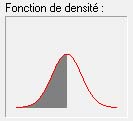
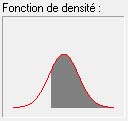
50% des observations sont inférieures à la moyenne et 50% au-dessus. Par exemple, environ 50% des individus ont un QI entre 0 et 100 (zone grisée) et 50% un QI plus haut que 100 (zone non grisée).
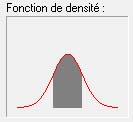
68% des observations tombent entre -1 et +1 écart-type de distance à la moyenne. Par exemple, 68% des individus ont un QI entre 85 et 115 (zone grisée).
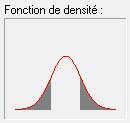
Réciproquement, les 32% d'individus restant sont à plus d'1 écart-type de distance, par défaut (zone grisée à gauche) ou par excès (zone grisée à droite), soit, en termes de QI, à moins de 85 ou à plus de 115.
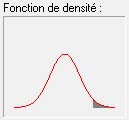
Si l'on prend 2 écarts-types, c'est 95% des observations qui tombent dans l'intervalle [m-1 écart-type; m+1 écart-type]. D'où moins de 2,5% d'individus ayant un QI plus grand que 130 (zone grisée à droite).
On peut aussi raisonner dans l'autre sens.
Prenons par exemple une mesure politique visant à amener 80% d'une classe d'âge au bac. Connaissant la distribution du QI, imaginons qu'on amène au bac tous les individus ayant le QI le plus haut (ce qui n'est évidemment pas le cas puisque de nombreux surdoués sont en échec scolaire). Cela correspond à la zone grisée du graphique. On voit alors que l'on donnera le bac à des individus dont le QI sera d'environ 88.
5.3. Distribution du t de Student
La distribution normale s'applique dès lors qu'un grand nombre de mesures sont prises et que certaines conditions sont remplies. Malheureusement, dans de nombreuses expériences scientifiques, il est difficile, voire impossible, de procéder à de nombreuses mesures.
Un mathématicien britannique, William Gosset, a découvert au début du XIXe siècle une statistique dont la distribution est plus représentative de ce qui se passe lorsque l'on a de petits échantillons : le t de Student.1 Vous retrouverez cette distribution dans les cours de statistiques inférentielles, et probablement tout le long de vos études. Pour le moment, bien que nous n'étudierons pas comment la calculer, elle nous sera bien utile pour illustrer le fait qu'une distribution peut varier systématiquement en fonction de divers paramètres. Ainsi, la distribution possède une certaine forme lorsqu'elle concerne un petit nombre d'observations et tend à ressembler à la distribution normale lorsque le nombre d'observations concernées augmente.
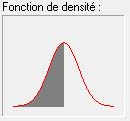
La figure ci-contre montre une distribution de
t
théorique pour un échantillon de 68 observations (techniquement ce paramètre est en fait une notion légèrement différente d'un simple nombre d'observations, et qu'on appelle degré de liberté et qui pour la distribution de
t
correspond généralement au nombre d'observations moins 1. Mais il n'est pas utile d'entrer dans ces détails pour ce cours). On voit qu'elle se distingue difficilement à l'œil nu de la distribution normale vue plus haut.
Pour mieux se rendre compte des différences subtiles induites par le paramètre que constitue le nombre de degrés de liberté, comparons deux distributions de t pour respectivement 2 et 1000 degrés de liberté :
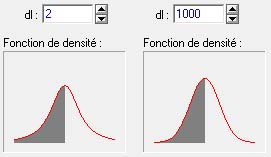
On voit aisément que la distribution à 1000 degrés de libertés (à droite) est légèrement plus haute, plus large, mais aussi que ses extrémités tendent plus vers zéro. En pratique, il devient difficile de la distinguer d'une distribution normale ordinaire.
1 Le nom de "Student" provient du fait que William Gosset était salarié du fabricant de bière Guiness, dont la politique était alors d'interdire la publication scientifique des travaux de ses employés. Gosset a donc publié ses travaux sous le pseudonyme de Student.
5.4. La distribution du Khi² et démonstrations vidéos
Cette distribution s'utilise notamment pour tester des hypothèses sur les variables nominales.
La distribution du  dépend d'un seul paramètre, le nombre de degrés de libertés. Le nombre de degrés de liberté étant directement une fonction du nombre de modalités de la (ou des) variable(s).
dépend d'un seul paramètre, le nombre de degrés de libertés. Le nombre de degrés de liberté étant directement une fonction du nombre de modalités de la (ou des) variable(s).
La symétrie de cette distribution augmente avec le nombre de degrés de libertés. Pour le moment, nous n'avons pas besoin de détailler plus cette distribution qui sera surtout utilisée dans les statistiques inférentielles, à partir du L2.
(Encore en réparation) Pour terminer cette introduction aux distributions, Voici une démonstration vidéo de l'évolution de quelques distributions lorsque les paramètres qui les définissent varient. Vous pouvez à tout moment mettre en pause et/ou relancer la diffusion en utilisant les boutons et la barre de contrôle situés sous la zone de vidéo.
Il existe de très nombreuses autres distributions pertinentes pour les sciences humaines, mais que nous ne les verrons qu'en temps utile.
6. Techniques de recodage des données
Objectif. Présenter la notion de recodage et l'illustrer par un ensemble des principales techniques utilisées pour transformer des données.
Prérequis. Aucun.
Résumé. Un premier écran présente la logique générale et l'utilité de la technique du recodage. L'écran suivant présente des transformations de variables par application de fonction, ce qui sert en particulier pour normaliser des distributions afin de pouvoir appliquer dessus diverses techniques statistiques qui exigent la normalité. Le troisième écran présente la technique de centration-réduction. Enfin, le dernier écran expose des techniques de recodage opérant sur la base des effectifs. Il existe aussi des techniques de classification fondées sur des analyses statistiques plus sophistiquées (classification hiérarchique, nuées dynamiques, ...) mais ces techniques ne sont a priori pas du niveau L1 et nous ne les verrons pas ici.

Lorsque vous ouvrez un logiciel de statistique, vous trouvez souvent parmi les menus des options avec des intitulés du type "recoder des données" ou "transformer des variables". Il peut s'agir aussi de libellés qui constituent des cas particuliers de recodage ou de transformation de variable comme "centrer-réduire","remplacer les valeurs manquantes", etc. Cet article a pour objectif d'expliquer pourquoi on a besoin d'employer de telles techniques ainsi que de présenter les principales méthodes de recodage des données.
6.1. Pourquoi recoder des données ?
Les raisons de procéder à un recodage des données sont très diverses.
1.1. Éliminer du bruit inutile
Lorsque l'on agrège les notes obtenues par un individu à plusieurs épreuves (par exemple à des tests psychologiques), l'opération de moyennage va souvent nous donner un résultat avec un certain nombre de décimales, par le seul jeu des opérations mathématiques. Mais, en fait, cette précision n'a strictement aucun sens psychologique. Par exemple, imaginez une épreuve du bac, où l'on teste les performances en mathématique, physique, anglais, etc. Lorsqu'on calcule ensuite la moyenne de l'élève, on peut trouver quelque chose comme 10,24583. Quel sens donner à ces chiffres ? Si l'on prend le 10, on voit à quoi ça correspond : la personne a « la moyenne », et donc on pourra lui donner le bac. Mais que signifie le 0.24583 ? Pas grand-chose pour le 2, encore moins pour le 4 et au-delà, on gagnerait en fait à se passer de cette pseudo-précision qui représente largement plus du bruit que de l'information réelle. D'où l'idée d'arrondir.
Mais arrondir n'est que le premier niveau de l'élimination du bruit. Par exemple, dans de nombreux cas, on peut demander aux sujets de donner une note sur une échelle qui va de 0 à 100, par degrés de 1 :À quel degré aimez-vous les patates bouillies ? 0 « pas du tout », 100 « j'en suis fou »... Même si les sujets donnent une valeur entière, donc qu'il n'est pas possible d'arrondir, en pratique, nous ne distinguons pas tant de degrés dans nos appréciations. Sur nos propres données, nous avons par exemple pu constater que la précision avec laquelle des médecins évaluent le risque d'une maladie dépasse rarement 5% (Raufaste, Da Silva Neves, & Mariné, 2003).
1.2. Pour pouvoir appliquer certaines techniques de calcul
Dans un certain nombre de cas, on peut souhaiter pratiquer des analyses qui requièrent que les variables prennent des valeurs discrètes. Par exemple, l'analyse de variance utilise habituellement des variables prédictrices ayant un tout petit nombre de modalités. Ou encore, vous voulez comparer les scores sur une variable dépendante (par exemple la performance scolaire) d'individus ayant un QI plus élevé que la moyenne contre ceux ayant un QI plus bas que la moyenne. Le QI étant une variable prenant de très nombreuses valeurs, il sera plus simple alors de recoder le score brut de QI en deux valeurs, par exemple 1 pour ceux qui ont moins que la moyenne et 2 pour ceux qui ont plus que la moyenne.
Dans d'autres cas, la variable de départ a très peu de modalités, mais celles-ci se présentent sous une forme qui n'est pas compatible avec les formats utilisés par le logiciel de statistique que vous voulez utiliser. Par exemple, imaginons que vous ayez les libellés « Homme » et « Femme » pour coder le sexe des individus. Or de nombreux logiciels de statistiques travaillent avec des valeurs numériques, mais lorsqu'il s'agit de variables nominales. En reprenant le codage classique de l'INSEE, on pourra alors par exemple recoder 1 pour les hommes et 2 pour les hommes.
Un autre cas important du besoin de recodage est lié aux pré-requis d'utilisation de certaines techniques. Par exemple, de nombreuses techniques statistiques supposent que les données soient normalement distribuées. Or dans souvent les données ne le sont pas. On peut donc appliquer diverses transformations pour donner une forme normale à la distribution.
1.3. Pour pouvoir comparer des données entre elles
De plus en plus, en psychologie cognitive, on utilise des appareils permettant d'enregistrer les mouvements oculaires pour savoir, en temps réel, ce que les sujets sont en train de regarder. Des informations précieuses sont apportées par les diamètres pupillaires qui, à éclairage constant, traduisent des variations émotionnelles ou des variations d'effort dont les sujets ne sont même pas conscients. Le problème est qu'on ne peut pas directement comparer les diamètres pupillaires d'un individu à l'autre puisque au départ les différents individus n'ont pas les yeux de la même taille. Comment faire ? Une solution consiste alors à appliquer une opération appelée centration-réduction, qui a pour effet, avant même de commencer les calculs de comparaison, de ramener les mesures prises sur les différents sujets à quelque chose qui soit indépendant de la taille de leur œil.
Nous allons maintenant passer maintenant à la page suivante pour voir de plus près quelques techniques de recodage.
6.2. Recodage par application de fonctions
Nous sommes ici dans le cas où nous avons une distribution qui n'est pas tout à fait normale alors que nous souhaitons appliquer une méthode statistique qui présuppose la normalité. Une façon simple de faire consiste à examiner la structure de la distribution et, si possible, à choisir une transformation mathématique telle qu'après l'avoir appliquée à chaque donnée, la distribution résultante ressemblera plus à une distribution normale.
Dans cette logique, la première chose à faire est de regarder le type de distribution pour pouvoir choisir la fonction mathématique adéquate.
2.1. Léger biais à gauche.
À titre d'exemple, examinons la distribution suivante, réalisée sur 1000 individus dont les valeurs sont stockées dans une variable nommée « V2 » :
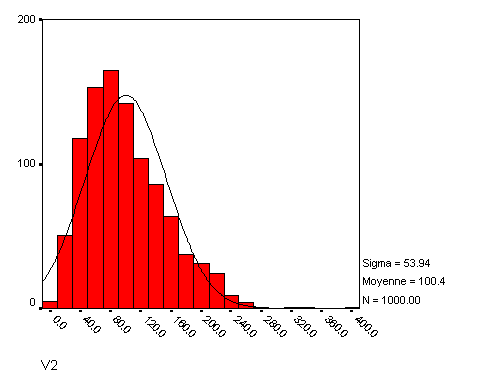
Nous voyons une forme en cloche, un peu comme une distribution normale, mais on voit aussi que l'histogramme diffère légèrement de la courbe gaussienne qui lui a été superposée. En particulier, l'histogramme semble dévié vers la gauche alors que la distribution normale est symétrique. On voit aussi qu'il existe quelques valeurs un peu perdues tout à droite alors que de telles valeurs devraient être très rares, car très éloignées de la moyenne (ici à 100 et avec un écart-type d'environ 54, cela place les valeurs extrêmes à environ 6 écarts-types de la moyenne, ce qui est considérable. D'ailleurs, si nous demandons à calculer les statistiques descriptives sous SPSS, nous obtenons un coefficient d'asymétrie de 0.90 ce qui reste acceptable, mais n'est pas parfait, et un coefficient d'aplatissement de 1.13, ce qui n'est pas très satisfaisant (idéalement la valeur absolue de l'asymétrie comme de l'aplatissement devraient rester inférieure à 1).
Sur une telle distribution, la fonction racine peut donner de bons résultats. Donc à chaque observation, on va appliquer la transformation suivante :
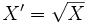
Par exemple, si la valeur de Xi était 400, la valeur de X'i sera 20. On obtient alors une variable recodée que nous allons nommer « V2R », dont voici la distribution :
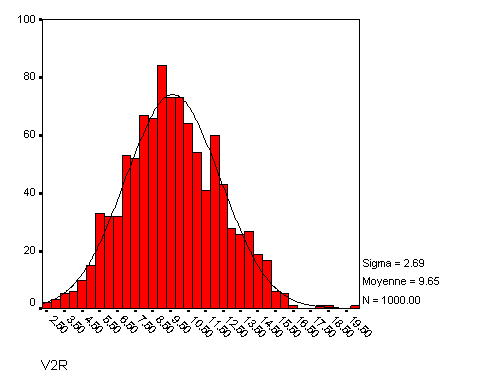
Fort logiquement, cette variable recodée varie maintenant entre 0 et autour de 20. Mais surtout, nous remarquons que l'histogramme obtenu ressemble beaucoup plus à une distribution normale, que ce soit en termes de symétrie qu'en termes d'aplatissement. Si nous demandons à SPSS de nous calculer les coefficients d'aplatissement et d'asymétrie de cette nouvelle variable, nous trouvons respectivement 0,16 et -0,16 ce qui tout à fait acceptable. À partir de là, si nous procédons à nos tests avec cette variable, les méthodes qui exigent la normalité comme condition pourront s'appliquer avec beaucoup plus de fiabilité.
Un point important est que la fonction Racine que nous avons utilisée préserve l'ordre des observations. Formellement, nous pourrons écrire que pour deux valeurs X1 et X2 positives,
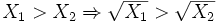
Ce point sera très important lorsqu'il s'agira d'interpréter les résultats obtenus en utilisant la variable recodée. Il faut être conscient que certaines transformations ne possèdent pas cette propriété et qu'il faut donc interpréter les résultats obtenus avec prudence.
2.2. Fort biais à gauche.
Considérons maintenant la variable V3, dont la distribution est la suivante :
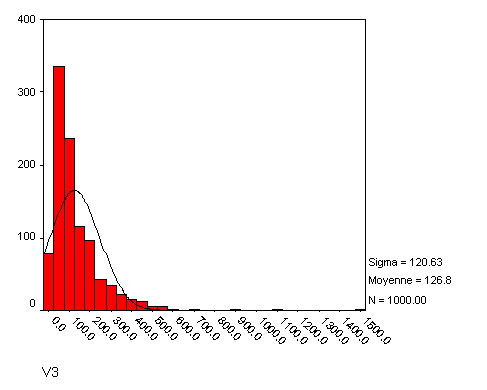
Cette fois, le biais à gauche est très marqué, probablement trop pour que l'application d'une fonction racine soit suffisante pour redresser la distribution. L'asymétrie est à 3,4, quant à l'aplatissement il s'envole à plus de 23 !! Nous pouvons cependant utiliser une autre fonction, plus appropriée à ce cas : le logarithme naturel. À chaque observation, on va appliquer la transformation suivante :
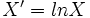
Par exemple, si la valeur de Xi était 1000, la valeur de X'i sera 6,90. On obtient alors la distribution suivante :
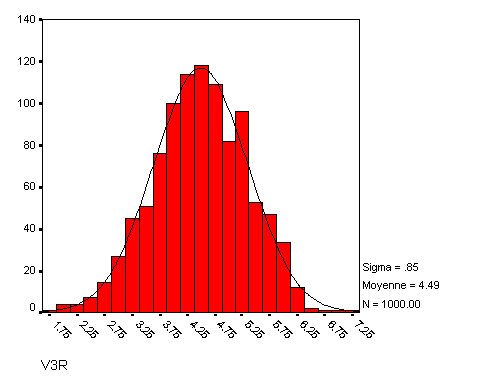
Là encore, nous avons une distribution largement plus en accord avec ce qu'on attend généralement d'une distribution dite normale. Les nouvelles valeurs d'asymétrie et de distribution que nous obtenons sont respectivement -0,11 et -0,12 ce qui est excellent. Notons que la fonction logarithme, comme la fonction racine, préserve l'ordre des observations.
Il faut cependant être conscient que ces transformations ne sont pas toujours applicables. Ainsi la fonction racine comme la fonction log ne peuvent pas s'appliquer à des valeurs négatives (vous obtiendrez une erreur si vous essayez d'appliquer ces fonctions sur des valeurs négatives). La fonction log ne peut pas s'appliquer à des valeurs nulles non plus.
2.3. Distribution en i
Dans un certain nombre de cas, la distribution sera biaisée à gauche, mais sans retomber comme dans une normale, ce qu'on appelle une courbe en i (par analogie évidente avec la forme scripte de la lettre i). En voici un exemple :
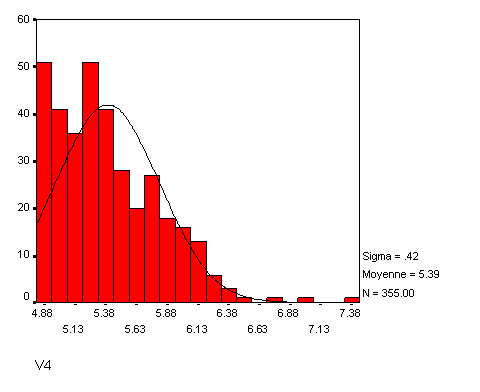
Dans ce cas, les fonctions précédentes risquent de ne pas marcher. Une solution alternative consiste alors à utiliser la fonction inverse (X' = 1/ X) peut donner des résultats satisfaisants :
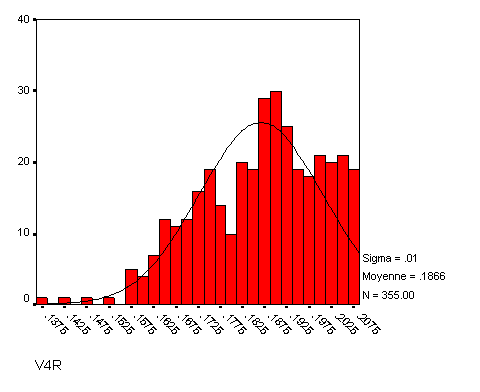
Sur cet exemple, vous pouvez avoir l'impression que le résultat n'est pas très concluant, mais si l'on demande les indices d'aplatissement et d'asymétrie, on voit qu'ils passent de 0,92 et 1,08 avant la transformation à -0,52 et -0,22 après, ce qui est clairement mieux. Cela dit, dans mon expérience en psychologie, les distributions en i et en j sont de mauvais pronostic. Souvent le caractère en i (resp. en j) résulte en effet d'un effet plancher (resp. un effet plafond), c'est-à-dire que beaucoup de sujets ayant donné la valeur la plus basse possible (resp. la plus haute), la distribution est tassée et rien ne pourra y faire, sauf à entrer dans de la cuisine plus radicale, à savoir utiliser des transformations qui ne préservent pas l'ordre des observations.
2.4. Distributions biaisées à droite
Les fonctions que nous avons évoquées précédemment s'appliquent pour corriger des biais à gauche. Que faire lorsque le biais est à droite ? Une solution très simple consiste à renverser d'abord les valeurs, afin d'obtenir une distribution biaisée à gauche, après quoi il suffit d'appliquer les méthodes précédentes.
Le renversement s'obtient très facilement en prenant la plus forte valeur de la distribution et en appliquant le complémentaire à cette valeur, soit
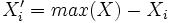
Il suffit alors d'appliquer la fonction vue précédemment, racine, log ou inverse selon les cas.
6.3. La centration-réduction
3.1. Pourquoi centrer-réduire ?
Le principal avantage de la centration-réduction est de rendre comparables des variables qui ne le seraient pas directement parce qu'elles ont des moyennes et/ou des variances trop différentes.
Un autre avantage, mais qui dépasse le niveau du présent cours, est relatif à la régression à plusieurs prédicteurs, lorsque l'on envisage d'étudier les interactions entre VI. Dans ce cas, il est conseillé de commencer par centrer-réduire les prédicteurs avant de calculer les termes d'interaction.
3.2. Qu'est-ce que la centration ?
On appelle centration l'opération qui consiste à retirer de chaque valeur d'une variable la moyenne de la variable.
Imaginez une variable normale de moyenne m et d'écart-type s. Si à chacune des valeurs de la variable, on retire la valeur constante m, on obtient une nouvelle variable qui, par les propriétés de la moyenne, aura pour moyenne 0. Son écart-type, par contre, vaudra toujours s.
3.3. Qu'est-ce que la réduction ?
On appelle réduction l'opération qui consiste à diviser chaque valeur d'une variable par l'écart-type de la variable.
Imaginez une variable normale de moyenne m et d'écart-type s. Si on divise chacune des valeurs de la variable par la constante s, on obtient une nouvelle variable qui, par les propriétés de la moyenne, aura pour moyenne m / s et pour écart-type 1.
Une autre propriété importante de la réduction est d'éliminer l'unité de la variable. Par exemple, si la variable est une taille, disons en mètres, alors l'unité de l'écart-type est aussi en mètres. Du coup, en divisant des mètres par des mètres, on obtient un nombre sans unité. De ce fait, s'il devient possible de comparer les dispersions de deux variables alors même qu'elles n'étaient pas initialement mesurées avec les mêmes unités.
3.3. Qu'est-ce que la centration-réduction ?
C'est tout simplement l'application combinée d'une centration puis d'une réduction. Ainsi, à chaque valeur Xi on fera correspondre une valeur dite centrée-réduite, que l'on note usuellement par la lettre Z :
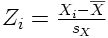
La distribution ainsi obtenue aura pour moyenne 0 et pour écart-type 1. Chaque note représentera directement une distance à la moyenne exprimée en écarts-types. Par exemple, une valeur de -3,2 signifie que pour cet individu la valeur mesurée était 3,2 écarts-types plus bas que la moyenne.
Notons que la plupart des logiciels de statistique, comme par exemple R, jamovi ou Statistica, fournissent des fonctions qui opèrent directement une centration-réduction sur les variables que vous leur indiquez.
6.4. La répartition en classes sur la base des effectifs
L'idée générale de la répartition en classes est que l'information portée par les nombres initiaux est inadéquatement riche (i.e., elle porte plus de bruit que d'information réelle). Toutefois, la logique de classification n'est pas du tout la même selon qu'on cherche à produire des classes sur la base des effectifs qu'elles contiendront, ou sur la base de leurs propriétés propres.
4.1. Répartition en classes d'effectif égal
Une catégorisation simple consiste à déterminer plusieurs classes d'effectif égal. En général, ce genre de classification est opérée sur la base d'une variable au moins ordinale (c'est-à-dire telle que les valeurs qu'elle prend respectent une relation d'ordre). La première opération est alors de reclasser les sujets selon leur rang sur la variable considérée (ce qui revient à faire un tri à plat). On découpe alors les classes selon le nombre souhaité, soit 1/ k sujets par classe lorsqu'il y a k classes. Cette opération s'appelle le quantilage et les limites de classes des quantiles. S'il y a dix classes, on parle alors de déciles. S'il y en a 4, on parle de quartiles. Cette procédure et ces termes avaient déjà été détaillés dans l'article sur les dispersions de variables ordinales.
Avec deux classes, cela donne 1/2=50% de sujets par classes. Ainsi, par exemple, on peut distinguer le groupe des valeurs fortes et des valeurs faibles en partitionnant la variable selon la médiane. Les 50% de sujets dont la valeur est supérieure ou égale à la médiane (par exemple) reçoivent une valeur arbitraire, disons 1, et les 50% restants reçoivent une autre valeur, disons 0.
Si l'on a des raisons de penser qu'une classification à 3 niveaux serait plus appropriée, il faut donc diviser les sujets en trois classes représentant chacune 33% de sujets, par exemple les sujets faibles, moyens et forts.
Et ainsi de suite en fonction du nombre de classes désiré.
4.2. Répartition en classes normalisées : la normalisation
Dans certains cas, on peut avoir besoin que les différentes classes possèdent une répartition à peu près normale, au sens où l'on trouve une proportion d'individus dans chaque classe sensiblement équivalente à ce que donnerait une distribution normale. Comme dans le cas de la classification en classes égales, tout commence par un tri à plat , c'est-à-dire que la première opération consiste à ranger les sujets par ordre croissant (ou décroissant, au choix) selon la variable considérée.
Connaissant la loi normale et connaissant le nombre de classes souhaitée, on peut alors déterminer les effectifs de chaque modalité. Par construction de la loi normale, et connaissant la moyenne et l'écart-type d'une distribution normale (c'est-à-dire connaissant ses paramètres), on sait quelle est la proportion d'effectifs compris entre telle et telle valeur. Par exemple, si la moyenne est 0 et l'écart-type 1, alors 68% des observations seront comprises entre les valeurs -1 et +1. En procédant dans l'autre sens, on peut mettre le pourcentage souhaité d'individus dans chaque classe. Ainsi, selon une technique nommée STANINE qui s'utilise dans certains tests, et notamment dans les tests psychotechniques utilisés en navigation aérienne depuis la seconde guerre mondiale, on classe les sujets en neuf classes selon leur performance. La logique est la suivante : Chaque classe couvre un demi-écart-type et la classe centrale, la classe 5, a pour centre la moyenne de la distribution. La classe 5 comprend donc tous les sujets qui ont une note comprise entre la moyenne -0.25 écart-type et +0,25 écart-type. La classe 4 comprend donc tous les sujets qui ont une note entre -0.75 écart-type et -0.25 écart-type. Par définition de la loi normale standard, on sait alors que la classe 1 doit contenir 4% de sujets, les 4% de sujets les plus faibles. La classe 2 doit contenir les 7% de sujets suivants, et ainsi de suite : 12% pour la classe 3; 17% pour la classe 4, 20% pour la classe 5; 17%; pour la classe 6; 12% pour la classe 7; 7% pour la classe 8; et enfin les 4% les plus forts reçoivent la classe 9. La distribution ainsi obtenue apparaît dans le graphique suivant :
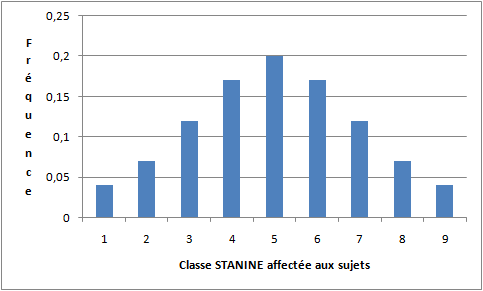
Comme vous le voyez, en procédant ainsi, on obtient une distribution d'allure normale même si les sujets n'avaient pas fourni des notes distribuées normalement à la base.
Par contre, cet avantage évident est compensé par des inconvénients qu'il ne faut pas se cacher. Par exemple, deux sujets ayant fourni des performances extrêmement similaires peuvent, par le seul jeu du recodage, se trouver classés dans des classes différentes. Réciproquement, tous les sujets d'une même classe se retrouvent avec la même note, celle de leur classe. De ce fait, le recodage ainsi réalisé produit des effets de bord non négligeable puisque deux sujets ayant fourni presque la même (voire la même) performance peuvent avoir des notes différentes alors que deux sujets ayant produit des performances assez dissemblables peuvent finalement se trouver avec la même note.
7. Dépendances et causalité
Objectifs. Au plan conceptuel, faire comprendre la notion de dépendance causale et pourquoi il est difficile d'affirmer une causalité à partir d'un simple constat de cooccurrences.
Prérequis. Les différents articles de la grande leçon Psychologie, statistique et psychométrie.
Résumé. Cet article introduit la notion de causalité en tant qu'objet scientifique qui induit une structure de dépendance entre observables. Il comprend quatre parties : après une introduction à la notion de cooccurrence, il présente quelques notions sur les relations de dépendance, leurs principales propriétés, et termine avec le cas particulier des relations de causalité.
7.1. Notion de co-occurrence
Techniquement, une cooccurrence est la simple occurrence simultanée de deux événements. Par exemple, je peux remarquer que Jean a beaucoup travaillé pour préparer son examen (événement 1) et je remarque que Jean a aussi obtenu une note brillante à son examen(événement 2). J'ai donc constaté une cooccurrence. En général, lorsque nous observons le monde, nous y cherchons des cooccurrences significatives, c'est-à-dire porteuses de sens. Par exemple, si mon but est de réussir mes examens, la cooccurrence précédente est significative car elle me suggère que c'est peut-être parce que Jean a travaillé qu'il a brillamment réussi son examen. Il s'agit là d'une hypothèse potentiellement utilisable. Si je travaille moi aussi, il est possible que j'obtienne aussi une note brillante.
En clair, le constat des cooccurrences suggère l'existence d'une relation de dépendance entre plusieurs variables. Toutefois, certaines relations de dépendance ont une valeur pronostique, au sens où, en connaissant l'évolution d'une variable, on pourra prédire l'évolution de l'autre variable. Examinons donc de plus près ce qu'on entend par relation de dépendance (ou au contraire, d'indépendance).
7.2. Les relations de dépendance
Lorsque nous étudions le monde, nous ne pouvons souvent rien faire d'autre que de constater des co-occurrences. La question fondamentale qui se pose alors au chercheur est de savoir passer du constat de cooccurrences à la création d'hypothèses sur le fonctionnement général du monde (c'est ce qu'on appelle l'induction) et comment tester ces hypothèses. Pour le praticien, la question est un peu différente, car les hypothèses générales ont le plus souvent déjà été produites par des chercheurs. Le psychologue ou le médecin n'inventent pas les maladies, ils se contentent de puiser dans leurs connaissances, la pathologie connue qui semble le mieux s'appliquer au cas du patient qu'ils ont en face d'eux. C'est ce qu'on appelle l'abduction. Mais qu'on soit chercheur ou praticien, il va falloir à un moment ou un autre tester les hypothèses. Il faut donc pouvoir vérifier si la relation qu'on suppose entre les variables est plausible ou non.
Concrètement, nous avons deux possibilités extrêmes : soit l'hypothèse d'une relation entre les variables est complètement fausse, soit elle est complètement vraie. Si elle est entièrement fausse, nous aurons ce qui s'appelle l'indépendance des variables. Si elle est entièrement vraie, nous aurons la dépendance parfaite. Examinons maintenant comment ces deux situations extrêmes se traduisent en termes de cooccurrences.
2.1. Dépendance de deux variables
Imaginons deux variables, disons l'âge et le revenu des adultes. Imaginons que ces deux variables soient parfaitement et positivement liées. Cela voudrait dire que plus une personne est âgée, et plus son revenu est élevé. Sous cette hypothèse, je pourrais prendre un échantillon d'adulte et pour chaque individu mesurer son âge et son revenu. Je vais donc disposer d'un ensemble de cooccurrences (de couples de données), une par personne. Par exemple, admettons que dans mon échantillon, les âges aillent de 30 à 50 ans. Admettons encore que les salaires soient répartis en trois catégories, 0 € à 999 € / mois; 1000 € / mois à 1999 € / mois, 2000 € /mois et plus.
Admettons que mes variables soient parfaitement liées, je m'attends à observer qu'à chaque fois que la variable âge est élevée, la variable revenu est élevée aussi. Je peux même observer que si deux individus n'ont pas le même âge, alors le plus âgé a aussi le revenu le plus élevé. Réciproquement, pour toute paire individus, si l'un n'a pas le même revenu que l'autre, alors celui qui a le revenu le plus haut est aussi le plus âgé. Clairement, si la structure des cooccurrences dans mon échantillon obéit à ces propriétés, je pourrai dire que les variables âge et revenu sont positivement liées.
Lorsque l'on se borne à constater la cooccurrence d'événements, on parle souvent alors de loi. Par exemple, la loi de Fechner relie l'intensité perçue d'un son et le logarithme de la puissance physique de ce son :
Notons que rien ne permet dans l'énoncé de cette loi de comprendre pourquoi il y a une relation logarithmique entre l'intensité perçue d'un son et le logarithme de son intensité physique. Pourquoi, après tout, le lien ne serait-il pas direct, sans passer par un logarithme ?
En fait, on parlera de loi surtout si cette co-occurrence est vraiment constatée régulièrement, et même à chaque fois qu'on la teste. Si l'on constate au contraire que cette relation arrive de temps en temps, mais pas toujours, on aura déjà plus de mal à la qualifier de loi.
Nous venons de voir ce que pouvait-être la dépendance. Mais que serait alors l'indépendance ?
2.2. Indépendance de deux variables
L'indépendance de deux variables est le fait que, quelles que soient les valeurs prises par une variable, les valeurs prises par l'autre variable n'en sont pas affectées.
Par exemple, je regarde la tranche basse de revenus, et je trouve des individus de tous les âges, indifféremment. Si je regarde les deux autres tranches de revenus, je fais le même constat. Dans ces conditions, rien ne permet de penser qu'il existe un lien entre les variables. Prenons le problème dans l'autre sens et examinons pour une tranche d'âge donnée les revenus correspondants. Si j'observe que quelle que soit la tranche d'âge, la distribution des revenus est la même, alors j'ai toutes raisons de penser que les variables âge et revenu sont indépendantes.
Autrement dit, le constat de co-occurrence nous sert à poser des hypothèses générales sur le monde, ou des hypothèses diagnostiques sur les causes potentielles des problèmes. Le problème est alors de pouvoir tester ces hypothèses, ce qui passe par une approche plus systématique des co-occurrences.
7.3. Propriétés des relations de dépendance
Nous avons vu que l'observation de co-occurrences peut suggérer l'existence ou la présence de relations de dépendance. Puisque nous souhaitons être capables d'identifier de telles relations de dépendance, ou au contraire pouvoir affirmer l'indépendance, il nous faut savoir caractériser les relations auxquelles nous sommes confrontés. Pour cela, il nous faut commencer par développer trois propriétés fondamentales des relations : leur force, leur direction, et leur forme.
2.3. Force de la relation
Admettons que la relation que nous supposons entre âge et revenus existe vraiment. Si nous considérons un vrai échantillon, il est néanmoins très peu plausible que tous les individus plus âgés gagnent plus. Certains individus jeunes peuvent avoir de hauts revenus et inversement, certaines personnes plus âgées peuvent gagner peu. Nous ne pourrons donc pas constater la dépendance stricte. Inversement, puisque la relation est globalement vraie, les personnes vont avoir tendance à gagner plus avec l'avancée en âge et donc, je n'aurai pas exactement la même distribution de revenus selon les tranches d'âges. Donc pas d'indépendance stricte non plus.
Nous pouvons alors généraliser un peu les concepts précédents et remplacer l'alternative entre indépendance totale et dépendance totale par quelque chose de plus nuancé : la notion de force de la relation, qui est en fait la force de la dépendance.
La question qui se pose alors est de produire un index, une valeur, qui nous permette de mesurer la force des relations. Il en existe plusieurs, selon le type de variables à mettre en relation, nous les verrons plus loin.
2.3. La forme de la relation
La forme de la relation est une propriété complexe que l'on peut décomposer en plusieurs sous-propriétés : direction, monotonie, linéarité, curvilinéarité, etc...
2.3.1. Le sens ou la direction de la relation
Dans l'exemple vu plus haut, plus l'âge augmente et plus les revenus augmentent. Si l'on traçait la courbe correspondant à une telle relation, elle serait vraisemblablement montante : les revenus seraient bas à gauche, vers les petits âges, et haute à droite, vers les âges plus avancés. On parlera alors d'une relation positive.
Bien évidemment, des relations peuvent être très fortes, mais dans le sens opposé. Par exemple, si l'on met en relation la catégorie socio-professionnelle et le chômage, on trouvera certainement une relation inverse : PLUS les individus appartiennent à une catégorie socio-professionnelle élevée, et MOINS ils tendent à être au chômage.
Il est clair que le sens de la relation est indépendant de la force : une relation peut être très forte et négative, très forte et négative, ou encore très faible et positive, ou très faible et négative.
2.3.2. La monotonie
La monotonie ou la non-monotonie d'une relation est le fait que la relation va toujours dans la même direction, c'est-à-dire toujours dans le sens positif ou toujours dans le sens négatif. C'était le cas pour la relation postulée plus haut, entre l'âge et le revenu. Mais il existe des relations non monotones. En psychologie par exemple, la loi de Yerkes-Dodson (1908) énonce ce fait bien attesté d'une non-monotonie entre le niveau de motivation et la performance : lorsque la motivation est très faible, la performance tend à être faible aussi. Au fur et à mesure que la motivation augmente, dans un premier temps, la performance tend à monter aussi (relation positive). Toutefois, cette monotonie est rompue lorsqu'un optimum de motivation est atteint. Au-delà de ce point, la motivation devient trop forte (comme lorsqu'un étudiant devient trop stressé par l'examen et se laisse perturber par ses émotions) et la performance commence à chuter de plus en plus avec l'augmentation de motivation, de façon monotone décroissante cette fois.
2.3.3. La linéarité : formes linéaires et non linéaires
Parmi les relations monotones, une forme de relation est particulièrement prisée, car elle se prête facilement aux traitements mathématiques et statistiques : la droite.
De façon intuitive, on dira qu'une relation est linéaire si elle ressemble à une droite. Plus formellement, une relation est linéaire lorsque tout accroissement sur une des deux variables s'accompagne d'un accroissement proportionnel (éventuellement négatif) sur l'autre variable. Les relations linéaires sont monotones.
Imaginez maintenant la courbe en U inversé qui caractérise la loi de Yerkes-Dodson vue plus haut. Elle ne peut évidemment pas se laisser décrire par une droite. On dira plutôt qu'elle est curvilinéaire, car elle décrit une courbe plutôt qu'une droite.
Il existe bien d'autres formes de courbes. Par exemple, la loi de Fechner vue plus haut décrit une courbe logarithmique. Les courbes d'apprentissages en psychologie suivent souvent une forme de fonction puissance, etc...
2.3. La symétrie
Cette dernière propriété est cruciale, car elle marque la distinction entre une dépendance mutuelle simple et la notion de causalité. En effet, si j'observe des co-occurrences rien ne me permet d'affirmer par ce seul fait la prééminence d'une variable sur l'autre. Par exemple, si j'observe que les gens heureux sont aussi en meilleure santé, sont-ils plus heureux parce qu'ils sont en meilleure santé ? Sont-ils en meilleure santé parce qu'ils sont plus heureux ? Le seul constat de la co-occurrence d'une bonne santé et du bonheur ne suffit pas à expliquer quoi que ce soit.
Dans certains cas, toutefois, cette prééminence existe de fait. Par exemple, puisque l'âge ne dépend que de la durée de vie, même si je constate une co-occurrence entre un âge élevé et un salaire élevé, il ne viendrait à personne d'affirmer que le salaire élevé cause l'âge. L'inverse au contraire peut être envisagé. Il y a donc, dans ce cas, dissymétrie entre les deux variables de la relation.
Un cas particulier d'asymétrie très important est utilisé par la méthode scientifique. Nous y reviendrons plus loin.
7.4. Dépendance et causalité
Parfois, la relation que nous imaginons entre deux variables n'est pas simplement l'existence d'une co-occurrence, mais traduit véritablement une causalité, c'est-à-dire que la variable A est une cause de la variable B . Par exemple,l'observation que plus les enfants sont âgés et plus leurs capacités intellectuelles augmentent, traduit une relation de cause à effet :c'est parce qu'il y a maturation biologique (avancée en âge de l'enfant) que les performances intellectuelles s'améliorent (par exemple du fait de la myélinisation des neurones).
Il est clair que pour le chercheur comme pour le diagnosticien, obtenir des relations véritablement causales est beaucoup plus intéressant que de constater de simples co-occurrences. En effet, une relation causale donne une perspective d'action, de prédiction. Si je sais que la cause d'une maladie est une bactérie, je peux aussitôt agir sur cette maladie en mobilisant mes connaissances sur ce qui lutte contre les bactéries. À l'inverse, si je sais que c'est un virus, je peux éviter de polluer l'environnement avec des antibiotiques qui seront de toute façon inefficaces. Cette plus grande efficience explique que l'étude logique de la causalité est un sujet qui remplit des manuels entiers de philosophes et de mathématiciens. Les psychologues, cognitivistes ou sociaux, travaillent aussi activement sur la perception de la causalité chez l'humain aussi. Nous n'avons pas l'ambition de passer ces travaux en revue ici. Tout ce qui nous intéresse est de vous donner quelques notions de base qui permettent de comprendre les problèmes posés par l'identification de la causalité à partir de données empiriques.
Afin de faire comprendre le problème qui se pose à nous, commençons par examiner différents types de relations causales. Nous partons du constat d'une co-occurrence régulière entre certaines valeurs d'une variable A et certaines valeurs d'une variable B. Comment peut-on les interpréter ?
3.1. Quelques interprétations au moyen de dépendances causales
Pour ces exemples, prenons l'observation de co-occurrence entre les valeurs d'une variable A (grossir) et une variable B (être fatigué). On observe que les gens qui grossissent tendent à être fatigués et réciproquement que les gens fatigués tendent à grossir. Comment interpréter cela ? Évidemment, une première interprétation consiste à se dire que la co-occurrence est purement fortuite : c'est par hasard qu'elle s'est manifestée dans nos données et si l'on recommence les mesures, il est probable que cette observation ne se réplique pas. Éliminer cette interprétation est un point très important qui fait l'objet des statistiques inférentielles et à ce titre ne ressort pas du présent cours. Aussi, dans la suite, supposerons-nous que la relation existe vraiment. La question est de l'interpréter.
La première forme de la relation causale est l'implication A → B. Les gens seraient fatigués parce qu'ils grossissent.
La deuxième forme de la relation causale est l'implication B→A. Cette fois, c'est la fatigue qui ferait grossir.
La troisième forme passe par l'intervention d'une troisième variable, C, qui cause à la fois A et B, d'où la cooccurrence observée. Par exemple, le facteur stress sera la cause commune : le stress engendre le sentiment de fatigue et d'un autre côté une hormone de résistance au stress aurait pour effet de stocker les graisses, d'où grossissement.
Une quatrième forme consiste à ce que la relation causale entre A et B soit réalisée par l'intermédiaire de la variable C : A → C → B. Par exemple, si on grossit ( A ), on tend à ronfler plus ( C ), ce qui secondairement dégrade la qualité du sommeil, d'où fatigue ( B ). Du coup, si quelque raison s'oppose à la réalisation de C suite à A, la réalisation de B ne surviendra pas non plus. Par exemple, si Marie veut lire tard à la bibliothèque ( A ), elle lira tard à la bibliothèque ( B )... sauf si la bibliothèque n'est pas ouverte (non C ) !
Enfin, une dernière forme de relation peut expliquer pourquoi, parfois, on observera B sans observer A
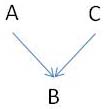
En effet, si A est absent, mais que C aussi peut être la cause de B, alors il suffit que C soit présent pour que B soit présent malgré l'absence de A.
On voit donc qu'il y a très loin du constat d'une co-occurrence à l'adoption d'une relation causale qui explique la co-occurrence de façon certaine.
3.2. La causalité permet la prédiction
Laissons maintenant de côté la question épineuse de l'identification du type de relation qui relie les variables A et B pour nous intéresser à une conséquence importante de la causalité : la capacité de prédire.
Intuitivement, si A et B sont en relation causale, disons que A est la cause de B, alors des variations sur A doivent s'accompagner de la présence de variations concomitantes sur B. Il existe une technique qui permet d'évaluer cette capacité de prédiction : la technique dite de régression, que nous examinerons dans l'article suivant.
8. Liaison entre deux variables
Objectif. Illustrer une méthode d'évaluation de la liaison de deux variables au moyen de la corrélation linéaire entre deux variables numériques. Les autres cas de liaison, c'est-à-dire lorsqu'au moins une des deux variables n'est pas numérique, seront abordés en détail sous forme d'une rubrique sur les liaisons entre variables non numériques de la section "Zoom sur...".
Prérequis. Les différents articles de la grande leçon Psychologie, statistique et psychométrie ainsi que ceux de la grande leçon Statistique descriptive.
Résumé. Cet article introduit une méthode classique d'évaluation de la force de liaison : la corrélation linéaire. L'article commence par introduire la notion de co-variation ainsi qu'une mesure numérique de cette covariation, la covariance. Ensuite, le coefficient de corrélation de Pearson est introduit et ses principales propriétés sont énoncées, en expliquant leur signification du point de vue de la force de liaison.
8.1. Covariation et covariance
1.1. Notion de co-variation
Imaginons deux variables extrêmement et positivement liées, par exemple le salaire et le pouvoir d'achat. On observe que dès que l'une monte, l'autre monte aussi. Réciproquement, dès que la première descend, la seconde descend aussi. Bien entendu, comme nous l'avons vu dans la leçon précédente, le lien peut être très fort, mais négatif (dès qu'une variable monte, l'autre descend).
Ainsi, si nous considérons deux variables en vue d'évaluer leur degré de liaison, on peut s'intéresser à la façon dont elles co-évoluent ou non, on dira à la façon dont elles « covarient ».
La covariation est le fait que les évolutions de chacune des deux variables présentent une certaine régularité. On l'aura compris, la covariation est un indicateur de liaison : plus la covariation est forte et régulière et plus on peut penser que les deux variables sont liées.
Une fois admis ce principe, la question qui se pose est de trouver un indicateur quantitatif de la covariation. Comment pouvons-nous faire pour mesurer la quantité de covariation qui relie deux variables ? Un premier élément de réponse nous est fourni par la notion de covariance.
1.2. Notion de covariance
Pour obtenir notre indice de covariation, il va falloir pour chaque individu statistique mesurer les variations sur une première variable X, les variations sur l'autre variable, Y, puis les combiner pour obtenir un indice agrégé. Enfin, il nous faudra agréger les mesures de covariation issues de chaque individu statistique pour obtenir une mesure globale de covariation.
1.2.1. Quantifier les variations sur chaque variable.
Imaginons que la variable ne varie pas. Tous les individus statistiques auraient donc la même valeur sur cette variable, valeur qui se trouverait aussi être la moyenne. Imaginons que cette variable commence à varier un petit peu. On trouvera donc certaines valeurs un peu éloignées de la moyenne par excès, d'autres un peu éloignées de la moyenne par défaut. Si la variable varie beaucoup, on trouvera de plus en plus d'individus ayant produit une valeur très éloignée de la moyenne. Sur cette base, il paraît donc assez naturel d'utiliser l'écart à la moyenne pour quantifier le degré de variation manifesté par un individu donné.
Soient
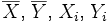
respectivement la valeur moyenne constatée sur la variable X, la valeur moyenne constatée sur la variable Y, la mesure de la variable X obtenue sur le ième individu, et enfin la mesure de la variable Y obtenue sur le ième individu.
La mesure de variation sur la variable X pour l'individu i peut donc être donnée directement par la valeur
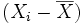
De même, la mesure de variation sur la variable
Y
pour l'individu
i
peut être donnée par la valeur
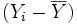
Notons que ces deux valeurs sont signées, au sens où un écart dans le sens où la valeur est plus grande que la moyenne aura un signe positif, tandis qu'une variation telle que la mesure est plus petite que la moyenne donnera un écart négatif.
1.2.2. Combiner les variations sur chaque variable.
Nous nous intéressons ici à obtenir une mesure de la liaison, donc à mettre en relation les variations sur une variable avec les variations sur l'autre variable, ce qui suppose de combiner les deux mesures précédentes. Par ailleurs, nous avons vu dans la leçon précédente qu'une liaison entre variable possédait une certaine force et une certaine direction. Il serait donc avantageux que l'indice que nous sommes en train de construire capture cette direction. Autrement dit, il ne devrait pas donner le même résultat lorsque les variations sur X et Y vont dans le même sens (par exemple lorsque les deux variables augmentent) et lorsqu'elles vont en sens contraire (par exemple, l'une monte et l'autre descend).
Une solution de combinaison très simple qui respecte ces propriétés est la multiplication :
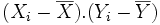
En effet, si l'on multiplie deux nombres de même signe, le produit sera positif tandis que si l'on multiplie deux nombres de signes opposés le produit sera négatif. Ainsi, le signe du produit des écarts à la moyenne sera positif si les deux mesures sur X et sur Y sont du même côté de leur moyenne, et de signe négatif si l'une est plus grande que sa moyenne tandis que l'autre est plus petite que sa moyenne.
1.2.3. Combiner les variations sur l'ensemble des sujets
Jusqu'ici, nous avons obtenu un indice qui caractérise la covariation au niveau de chaque individu. Finalement, pour avoir une vue d'ensemble de la covariation des deux variables, il nous reste donc à agréger les indices individuels en un indice global. Pour ce faire, une solution naturelle est d'utiliser la moyenne, donc de calculer la somme de chaque indice individuel puis de diviser par le nombre d'individus de la population. Cela nous donne un indice qui est la covariance des deux variables dans la population considérée :
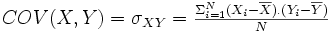
Comme vous pouvez le noter sur la formule ci-dessus, la lettre qui est utilisée pour caractériser la covariance est la lettre grecque sigma, dont nous avions vu qu'elle était utilisée pour dénoter l'écart-type d'une variable. Nous allons voir maintenant que cela n'est pas un hasard.
1.3. Relation entre covariance et variance
Que se passe-t-il si j'essaie d'estimer la covariance d'une variance avec elle-même ? Évidemment, je m'attends à trouver une liaison parfaite. Donc d'une certaine façon, la covariance d'une variable avec elle-même devrait me donner une idée de la plus parfaite liaison qu'il est possible d'avoir avec cette variable. Appliquons donc notre formule de covariance à une variable A dont on va mesurer la covariance avec elle-même. Nous aurons alors
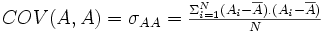
Il est clair que le terme
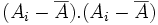
peut se réécrire
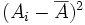
et donc que
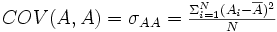
Au cours de la présente grande leçon, nous avons déjà posé la question de la quantification des variations. C'était lorsqu'il s'agissait de mesurer la dispersion d'une variable, dans l'article sur les indices de dispersion. Il est en effet assez intuitif que variation et dispersion recouvrent des concepts très similaires : plus il y a de variations, plus il y a de dispersion et réciproquement. De ce fait, si je dispose d'un indice de mesure de la dispersion, je dispose par là-même d'un indice de quantification des variations. Dans le cas d'une variable numérique, nous avons vu que l'indice pertinent était la variance dont la formule était la suivante :
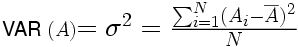
Si vous comparez les deux formules, celle de la variance et celle de la covariance d'une variable avec elle-même, vous voyez qu'elles sont rigoureusement identiques.
8.2. Limites de la covariance comme indicateur de liaison
Nous avons donc construit un indice de liaison, la covariance, qui possède une propriété intéressante, il est positif si les deux variables varient dans le même sens et négatif sinon. Autrement dit, la covariance nous donne la direction de la relation. Mais ce qui serait intéressant, ce serait de pouvoir disposer d'une évaluation de la force de la relation. Est-ce que la covariance est un bon indice pour cela ?
2.1. Un exemple numérique
Pour nous convaincre que non, prenons un exemple numérique, qui nous permettra au passage de vérifier notre compréhension des formules vues plus haut. Soient trois variables, X, Y, et Z, mesurées chacune sur les cinq mêmes individus :
| X | Y | Z |
| 1 | 2 | 4 |
| 2 | 3 | 6 |
| 3 | 4 | 8 |
| 4 | 5 | 10 |
| 5 | 6 | 12 |
leurs moyennes respectives sont 3, 4 et 8. En fait, les variables X et Y ne diffèrent que d'un point : toute mesure sur Y est égale à la mesure sur X augmentée de 1. De même, Y et Z ne différent que d'un facteur 2 : on obtient toute mesure de Z en doublant la mesure obtenue sur Y. X et Y d'un côté, X et Z de l'autre sont donc parfaitement liées.
Nous calculons alors, pour chacune des valeurs de chaque variable, l'écart à la moyenne de la variable :
| X-m(X) | Y-m(Y) | Z-m(Z) |
| -2 | -2 | -4 |
| -1 | -1 | -2 |
| 0 | 0 | 0 |
|
1
|
1 | 2 |
| 2 | 2 | 4 |
L'étape suivante est de calculer les produit des écarts à la moyenne pour X et Y d'un côté, X et Z de l'autre côté :
| (X-m(X))*(Y-m(Y)) | (X-m(X))*(Z-m(Z)) |
| 4 | 8 |
| 1 | 2 |
| 0 | 0 |
| 1 | 2 |
| 4 | 8 |
Finalement, les deux covariances sont données en faisant la moyenne de chacune des deux colonnes, soit Cov(X, Y)=2 et Cov(X, Z)=4.
Comme ces deux valeurs sont très différentes l'une de l'autre (à part leur signe qui est le même, fort heureusement), nous pouvons donc voir que la covariance n'est pas un indice très utilisable pour rendre compte de la force de la covariation. C'est pourquoi nous allons nous tourner vers un raffinement de la covariance : la corrélation.
8.3. La corrélation linéaire (définition et propriétés)
3.1. Définition
Le principal problème de la covariance, c'est que si on multiplie une des deux variables par deux (exemple précédent), la covariation des deux variables n'est pas affectée et pourtant la covariance elle-est affectée. Pour éviter cet effet, il faut standardiser la covariance en la divisant par la dispersion de chacune de deux variables. On obtient ainsi ce qu'on appelle le coefficient de corrélation linéaire :
En France, on l'appelle aussi coefficient de Bravais-Pearson, mais à l'étranger il est seulement connu sous le nom de coefficient de Pearson... et son origine est à chercher chez Francis Galton.
3.2. Propriétés remarquables et interprétation
3.2.1. Valeurs prises par le coefficient de corrélation
Le coefficient de corrélation varie entre -1 et +1, indépendamment des échelles des variables
 et
et
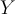 .
.
La valeur +1 traduit une corrélation linéaire positive parfaite, c'est-à-dire que toute variation d'une variable se traduit par une variation proportionnelle et de même direction sur l'autre variable.
La valeur -1 traduit une corrélation linéaire négative parfaite, c'est-à-dire que toute variation d'une variable se traduit par une variation proportionnelle et de direction inverse sur l'autre variable (si l'une monte, l'autre descend).
La valeur 0 signifie l'absence de corrélation linéaire (mais pas forcément l'absence de relation)
3.2.2. Chausse-trappe n°1 : corrélation n'est pas causalité !
Une erreur fréquente chez les débutants consiste à confondre corrélation et causalité : ce n'est pas parce que deux variables sont très liées (i.e., qu'elles corrèlent à +1 ou -1) que l'une est la cause de l'autre. Plusieurs possibilités différentes peuvent expliquer une corrélation très forte. Parmi ces possibilités, deux sont notables :
1°) l'effet du hasard : il est toujours possible qu'une corrélation observée très forte soit entièrement due au hasard. Il existe des techniques pour évaluer ce risque, mais elles ne sont pas au programme de ce cours.
2°) l'effet d'une troisième variable cachée. Supposons par exemple que l'on découvre une corrélation très forte entre la couleur des dents et le cancer du poumon. Serait-il raisonnable de penser que les dents jaunes causent le cancer du poumon ? Ou que le cancer du poumon fait jaunir les dents ? En fait, il existe une troisième explication : la consommation de tabac fait jaunir les dents ET cause le cancer du poumon.
3.2.3. Chausse-trappe n°2 : absence de corrélation linéaire n'est pas absence de liaison !
En présence d'une corrélation nulle, on pourrait être tenté de se dire qu'il n'y a pas du tout de relation entre les deux variables. Si cette possibilité existe, elle est néanmoins loin d'être la seule. En effet, le mode de calcul de la corrélation linéaire fait que ce coefficient détectera une liaison dans le cas où la forme de la relation est une droite, ou suffisamment proche d'une droite (d'où l'expression de corrélation linéaire).
La figure ci-dessous, par exemple, représente la parabole d'équation  . Autrement, à toute valeur de
. Autrement, à toute valeur de 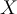 , on fait correspondre la valeur
, on fait correspondre la valeur 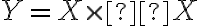 . La liaison est évidemment parfaite puisqu'on sait précisément quelle sera la valeur de
. La liaison est évidemment parfaite puisqu'on sait précisément quelle sera la valeur de
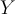 dès qu'on connait la valeur de
dès qu'on connait la valeur de
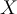 .
.
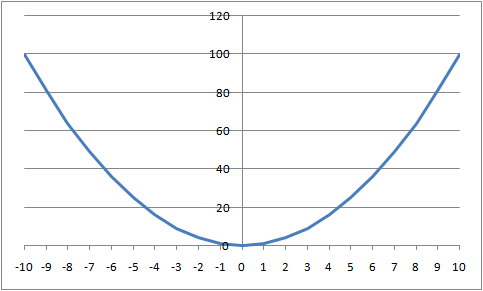
Or, le coefficient de corrélation sera alors de zéro ! En effet, le coefficient de corrélation mesure à quel degré toute augmentation sur une variable se traduit de manière régulière par un accroissement (ou une décroissance) proportionnelle sur l'autre variable. Si l'on a une parabole par exemple, les accroissements sur
 vont se traduire d'abord par une décroissance sur
vont se traduire d'abord par une décroissance sur
 (voir figure plus haut), puis dans un second temps par une augmentation sur
(voir figure plus haut), puis dans un second temps par une augmentation sur
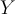 ! Au total, il y aura eu autant d'accroissements que de décroissance et le coefficient de corrélation sera annulé alors même que la dépendance était parfaite : connaissant une valeur de
! Au total, il y aura eu autant d'accroissements que de décroissance et le coefficient de corrélation sera annulé alors même que la dépendance était parfaite : connaissant une valeur de 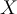 , on pouvait prédire parfaitement la valeur que prendrait
, on pouvait prédire parfaitement la valeur que prendrait
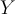 .
.
3.3. Stratégie de calcul
Vous pouvez trouver une démonstration d'une méthode simple pour le calculer, dans la section savoir-faire du présent cours, qui présente comment utiliser le tableur OpenOffice avec la fonction PEARSON().
8.4. La corrélation linéaire (Simulation)
Afin de vous permettre de développer une certaine intuition de ce que représente réellement le coefficient de corrélation, nous vous proposons la simulation suivante. Vous pouvez saisir une valeur de l'indice de corrélation dans la zone en violet. Chaque point du nuage représente une cooccurrence entre une valeur mesurée sur la variable 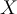 et une valeur mesurée sur la variable
et une valeur mesurée sur la variable
 . À chaque fois que vous cliquerez sur le bouton "cliquez", la simulation dessinera un nuage de points qui produirait la valeur de corrélation que vous aurez indiquée. Nous vous conseillons de jouer avec les différentes valeurs pour mieux vous rendre compte de ce que veut dire une valeur donnée. En particulier, essayez d'approcher -1 (-.999 par exemple) et +1 (.999 par exemple) afin de voir ce qui se passe aux valeurs extrêmes. Essayez aussi de vous rapprocher progressivement de zéro. Attention à ne pas dépasser les valeurs de -1 et +1, faute de quoi le dessin serait rendu impossible.
. À chaque fois que vous cliquerez sur le bouton "cliquez", la simulation dessinera un nuage de points qui produirait la valeur de corrélation que vous aurez indiquée. Nous vous conseillons de jouer avec les différentes valeurs pour mieux vous rendre compte de ce que veut dire une valeur donnée. En particulier, essayez d'approcher -1 (-.999 par exemple) et +1 (.999 par exemple) afin de voir ce qui se passe aux valeurs extrêmes. Essayez aussi de vous rapprocher progressivement de zéro. Attention à ne pas dépasser les valeurs de -1 et +1, faute de quoi le dessin serait rendu impossible.
8.5. Conclusion
Pour terminer ce tour d'horizon de la covariation, signalons que la corrélation linéaire a été présentée ici, car elle représente un peu le modèle de l'indice d'évaluation de la force et de la direction d'une relation. Toutefois, cela ne doit pas masquer le fait que lorsque les variables dont on veut évaluer la liaison ne sont pas toutes les deux numériques, il n'est pas toujours faisable de se ramener à une corrélation (nous verrons que cela reste néanmoins possible dans certains cas). Dans de nombreux cas, il existe cependant des indices dérivés de la corrélation et qui restent calculables.
Dans un certain nombre de cas, ces indices restent d'ailleurs interprétables assez simplement.
Plutôt que de rentrer immédiatement dans le détail de ces indices, nous avons fait le choix de les renvoyer à un article de la rubrique "zoom sur", en considérant qu'il s'agit surtout ici de faire comprendre les principes généraux.
9. Prédire une variable numérique : la régression simple
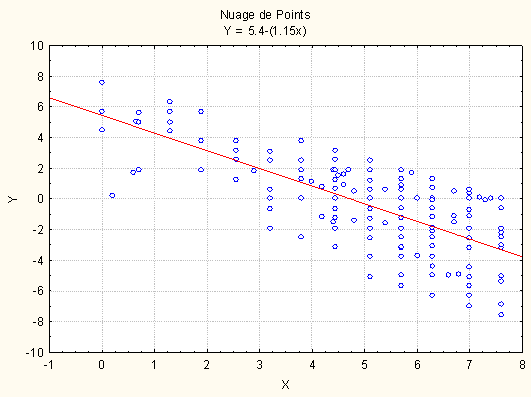
Objectif. Expliquer comment on peut prédire une variable numérique à partir d'une autre variable numérique. Illustrer
Prérequis. Les différents articles de la grande leçon Psychologie, statistique et psychométrie ainsi que ceux de la grande leçon Statistique descriptive.
Résumé. Cet article introduit la notion de courbe de régression. Le cas linéaire est ensuite examiné plus en détail.
9.1. La problématique de la régression
A. Prédire permet d'agir
Il existe deux mobiles fondamentaux pour acquérir de la connaissance. Le premier est le simple goût de la compréhension : on souhaite connaître parce que comprendre le monde procure directement un certain plaisir. C'est une seconde motivation de la connaissance que nous allons explorer ici : la connaissance nous permet d'acquérir un certain degré de contrôle sur le monde. Nous pouvons, grâce aux connaissances, augmenter la quantité de conséquences favorables qui risque de survenir suite à la situation actuelle, ou au contraire éviter les conséquences potentielles défavorables de la situation actuelle.
Dans le présent article, nous allons examiner comment utiliser les statistiques pour décrire le monde sous l'angle de la prédiction. Le problème est double :
produire les connaissances qui permettent de prédire
appliquer ces connaissances pour réaliser des prédictions
B. La prédiction s'appuie sur des indices
Pour réaliser la prédiction, nous avons besoin d'analyser l'état actuel du monde, puis d'établir une relation entre l'état actuel du monde et l'état futur du monde. Par exemple, je sais que si je lâche un objet maintenant, quelques instants après, il viendra s'écraser sur le sol. Les cas de prédiction intéressants ne sont pas aussi triviaux. Par exemple, si je suis médecin, connaissant une configuration de symptômes et de caractéristiques du patient, je vais m'intéresser à établir un pronostic, c'est-à-dire avoir une idée des chances de guérison du patient. En fonction de ce pronostic, et en fonction des moyens techniques disponibles, je vais pouvoir déclencher certaines actions. Même sans être médecin, nous faisons tous continuellement de la prédiction. Par exemple, si je suis au volant de ma voiture, je prends des indices sur le comportement des autres conducteurs autour de moi et j'en infère leur intention. Cette interprétation de l'intention des autres conducteurs me sert à prédire comment je dois piloter ma voiture pour me diriger dans le trafic efficacement et sans causer d'accident.
On peut aussi s'intéresser à la prédiction pour évaluer jusqu'à quel point il est possible d'utiliser une variable pour prédire une autre variable. Par exemple, imaginons un employeur qui fait passer des tests de QI lors des épreuves de sélection pour le recrutement. Il pourrait être tenté de recruter simplement les individus ayant le plus haut QI, sous l'hypothèse que ceux-ci sauront mieux s'adapter aux difficultés de leur vie professionnelle à venir. D'un autre côté, même si l'on sait que c'est globalement vrai, on sait aussi que la relation est loin d'être parfaite, car d'autres facteurs que les habiletés logico-mathématiques interviennent dans la réussite professionnelle. Selon les professions par exemple, la créativité, le contact humain, etc. peuvent constituer des prédicteurs de performance importants aussi que l'employeur pourrait donc être tenté de mobiliser dans son choix.
C. Formalisation du problème
Nous venons de voir que les connaissances qui pour réaliser des prédictions, il faut mettre en relation un état actuel du monde et un état futur du monde. Si nous réduisons le problème à sa plus simple expression, nous aurons donc une variable qui codera l'état actuel du monde et qui nous servira à prédire une autre variable qui codera l'état futur du monde.
Nous appellerons prédicteur la première variable. Dans la littérature, on trouve aussi les termes indice, ou encore, lorsque l'on suppose un lien causal entre l'état actuel et l'état futur, l'expression variable indépendante.
Nous appellerons variable prédite celle qui code l'état futur du monde. Dans la littérature, on trouve aussi le terme critère ou, en cas de relation causale, de variable dépendante.
Finalement, pour décrire l'ensemble de la question, il nous faut exprimer la relation qui existe entre la variable prédite, que nous noterons
Y, et la variable à prédire que nous noterons
X. On suppose alors qu'il existe une relation mathématique entre les deux, relation que l'on dénotera ici par la lettre grecque  :
:
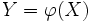
Ainsi posée, la question de la prédiction revient à chercher la nature de la relation  qui relie les variables X
et
Y, ou mathématiquement parlant, déterminer l'équation qui relie
X
et
Y.
qui relie les variables X
et
Y, ou mathématiquement parlant, déterminer l'équation qui relie
X
et
Y.
D. Principe de l'identification empirique de 
Pour étudier  empiriquement, nous allons prendre des mesures de
X
et des mesures de
Y. Par exemple, nous demanderons leur âge à un échantillon de participants, et nous estimerons combien ils ont de rides sur le visage. À l’issue de ce recueil de données, nous disposons donc d’un ensemble de couples de données, un couple par sujet. Ensuite, nous appliquons des méthodes statistiques, graphiques, etc. pour essayer de comprendre quelle est la nature de la fonction
empiriquement, nous allons prendre des mesures de
X
et des mesures de
Y. Par exemple, nous demanderons leur âge à un échantillon de participants, et nous estimerons combien ils ont de rides sur le visage. À l’issue de ce recueil de données, nous disposons donc d’un ensemble de couples de données, un couple par sujet. Ensuite, nous appliquons des méthodes statistiques, graphiques, etc. pour essayer de comprendre quelle est la nature de la fonction  .
.
La régression linéaire, méthode qui nous occupe ici, se caractérise par le postulat que la relation φ peut être approchée par une fonction affine (c'est-à-dire par une droite que, par abus de langage, nous appelons souvent fonction linéaire) dont les propriétés sont connues, puis à évaluer à quel point cette fonction est capable de rendre compte des données observées. En d’autres termes, on part du principe qu’il existe une droite
F
dont l’équation est une bonne approximation de 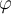 . Partant de cette hypothèse (et de quelques autres…) on applique des calculs mathématiques sur les données qui nous permettent d’évaluer les paramètres caractéristiques de F.
. Partant de cette hypothèse (et de quelques autres…) on applique des calculs mathématiques sur les données qui nous permettent d’évaluer les paramètres caractéristiques de F.
Dans un second temps, une fois F identifiée, on va évaluer à quel point
F
est ajustée aux données, c’est-à-dire à quel point
F
représente un bon modèle des données observées. Si cet ajustement est jugé satisfaisant, on pourra considérer, jusqu’à nouvel ordre, que la droite
F
est une bonne représentation de la fonction «vraie», j. Bien entendu, si  est trop différente d’une droite, on ne parviendra pas à trouver une droite
F
qui ressemble suffisamment à
est trop différente d’une droite, on ne parviendra pas à trouver une droite
F
qui ressemble suffisamment à  pour que l’on s’en satisfasse.
pour que l’on s’en satisfasse.
Dans une approche exploratoire pure, où l’on ignore a priori tout de φ, le simple fait d’appliquer cette méthode peut déjà constituer un premier apport de connaissances sur  . Plus tard, on pourra vouloir améliorer notre capacité de prédiction, et il se peut que l’approximation linéaire ne soit plus acceptable : on aura alors besoin d’explorer les cas où
F
n’est pas une droite, mais une fonction plus complexe, ce qui, pour l’essentiel, on sort alors du cadre du présent cours.
. Plus tard, on pourra vouloir améliorer notre capacité de prédiction, et il se peut que l’approximation linéaire ne soit plus acceptable : on aura alors besoin d’explorer les cas où
F
n’est pas une droite, mais une fonction plus complexe, ce qui, pour l’essentiel, on sort alors du cadre du présent cours.
Nous allons maintenant passer à l'analyse détaillée de la méthode de régression.
9.2. Notion de courbe de régression
A. Le nuage de points
Dans le cas le plus général, on pourrait souhaiter prédire plusieurs variables à partir de plusieurs prédicteurs et avec des relations mathématiques de toutes sortes entre les prédicteurs et les variables à prédire. Toutefois, au niveau d'un cours de L1, il est préférable de commencer par le cas le plus simple, dans lequel il n'y a qu'une variable à prédire et qu'un prédicteur, et dans lequel la nature de la relation est une relation affine. Autrement dit, nous nous plaçons dans le cas de la régression linéaire simple.
La figure ci-dessous représente un tel nuage de points réalisé à partir de 242 observations avec une variable à prédire qui varie entre -10 et 10, et un prédicteur qui varie entre 0 et 8. Attention au fait qu'il n’y a pas 242 points sur le graphique, car plusieurs observations peuvent correspondre à un même point.
S'il y a une relation entre X et Y, cela signifie que les valeurs de Y sont déterminées par les valeurs de X, aux erreurs de mesure près. Notons que, dans le cas général, la relation pourrait aussi bien être dans l'autre sens, à savoir que les valeurs de X soient déterminées par celles de Y. À l'inverse, nous avions vu dans l'article précédent, sur la corrélation, que l'on peut définir l'absence de relation comme étant le fait que les valeurs d'une variable ne sont pas affectées par les valeurs prises par l'autre variable. Autrement dit, quelle que soit la valeur Xi considérée, la distribution des valeurs de Y autour de Xi sera la même. Graphiquement parlant, le nuage de points ressemblera alors à un rectangle horizontal. Ici, on n'a pas l'impression d'un rectangle et on a l'impression d'une pente décroissante (on descend en allant vers la droite). La forme du nuage de points nous indique donc que l'idée d'une relation entre les deux variables n'est pas a priori saugrenue : il semble que les valeurs de Y ne soient pas distribuées au hasard selon les valeurs de X. La question qui se pose alors à nous est d'essayer d'analyse quelle pourrait être cette relation.
Pour cela, nous allons essayer de définir un peu plus précisément l'intuition que nous donne la vue du nuage de points. Il nous faut donc un concept qui permette de traduire un peu plus formellement l'idée que les valeurs d'une variable sont -- ou non -- distribuées de façon équivalente selon les valeurs de l'autre variable.
Un premier pas est de définir les notions de moyenne et variance conditionnelles.
B. Moyenne et variance conditionnelles
Si je considère une valeur donnée de X, disons par exemple 0 sur le graphique ci-dessus. Je vois pour cette valeur de X là, Y a pris trois valeurs, c'est-à-dire que l'on a trouvé des individus ayant obtenu 0 sur la variable X , mais ayant obtenu des valeurs différentes sur la variable Y. Du coup, il est possible de calculer la moyenne des valeurs de Y qui correspondent à chaque valeur particulière de X. C'est ce que l'on appelle la moyenne de Y conditionnelle à X. De la même manière, on peut calculer une variance de Y conditionnelle à X. Réciproquement, on pourrait s'intéresser aux valeurs que prend X pour une valeur de Y donnée. Cela nous permettra de calculer une moyenne de X conditionnelle à Y et une variance de X conditionnelle à Y.
C. Courbes de régression
Si l’on trace pour chaque valeur de X, le point correspondant à la moyenne des valeurs Y en cette valeur de X, les moyennes de Y conditionnelles en X donc, et que l’on joint ensuite ces points, on obtient une courbe dite courbe de régression de Y en X (voir figure ci-dessous). Si l'on imagine que X prédit parfaitement Y, alors la valeur moyenne de Y conditionnelle en chaque point de X devrait être la valeur prédite par la relation. Et par conséquent, la courbe de régression serait en fait la courbe qui exprime la relation entre X et Y. En pratique toutefois, les mesures empiriques sont toujours entachées de bruit, de sorte qu'il existe toujours une certaine quantité de variations autour de la moyenne conditionnelle (autrement dit, la variance conditionnelle n'est jamais nulle).
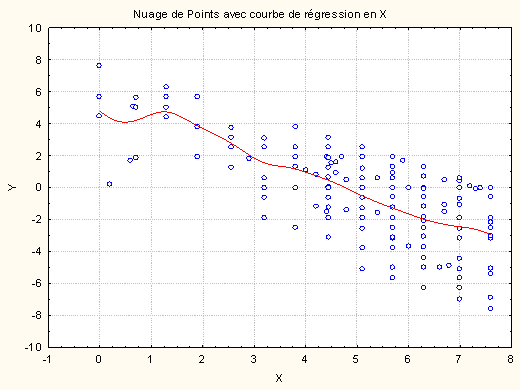
Dans l’exemple de la figure ci-dessus, la courbe de régression ne passe pas nécessairement au milieu des points d’une verticale donnée. Cela s’explique par le fait que chaque point est pondéré par le nombre d’observations correspondant. Un point présent dans beaucoup d’observations va donc plus « attirer » la courbe de régression que les autres points.
Réciproquement, on peut tracer la courbe de régression de X en Y et cette courbe de régression représente la meilleure estimation possible de la capacité de Y à prédire X.
Pour chaque point du nuage, sa coordonnée Yi (resp. Xi) peut se décomposer en une partie correspondant à la courbe de régression en X (resp. Y) plus une partie résiduelle. Exprimé en termes de variance, cela donne
Var (Y) = variance « expliquée par la courbe de régression » en X + Variance résiduelle
Ou encore
Var (X) = variance « expliquée par la courbe de régression » en Y + Variance résiduelle
9.3. Ajustement des courbes de régression
Lorsque l’on veut modéliser les données, la question qui se pose ensuite est de trouver l’équation des courbes de régression. Les courbes de régression correspondent généralement à des fonctions compliquées, mais on peut chercher à les approcher par des fonctions plus simples. Le principe général est de partir d’une forme de fonction connue et de chercher les paramètres qui ajustent le mieux possible les courbes obtenues aux courbes de régression.
Par exemple, si l'on part de l'idée que la courbe de régression, si l'on mettait de côté les erreurs de mesure, serait une droite, alors elle serait caractérisée par une équation de type
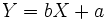
Il faudrait alors identifier les paramètres a et b pour connaître l'équation de la droite.
Si l'on imagine que la courbe de régression correspond à une parabole, l'équation cherchée serait de la forme :
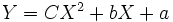
et dans ce cas, il faudrait trouver les valeurs des trois paramètres, a, b, et c.
L'idée générale pour identifier les paramètres est d'ajuster les valeurs des différents paramètres pour que l'erreur commise en appliquant l'équation obtenue soit minimale. Par exemple, imaginons qu'on décide que la courbe de régression de la figure précédente correspond en réalité à une droite et que cette droite a pour paramètre b =-0.5 et a =+4. Pour chaque individu i, on est alors en mesure de calculer pour chaque valeur de X la valeur de Y prédite par cette droite. On note cette valeur (prononcer « Y chapeau »)
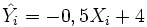
Maintenant, du fait de l'erreur de mesure, pour chaque observation une erreur de prédiction est commise, erreur appelée résidu et directement mesurable par l'écart entre la valeur prédite et la valeur observée :p
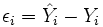
Finalement, l'idée de l'ajustement est de retenir le jeu de paramètres tel que l'erreur ε moyenne sera minimale. Dans le cas de la régression linéaire, on s'appuie sur l'idée d'une droite et donc le jeu de paramètres à trouver est le jeu des valeurs p a et b qui minimisent la fonction d'erreur. On emploie alors le terme de"droite de régression" pour décrire la fonction qui approxime la courbe de régression. Dans le cas particulier du nuage de points précédent, les paramètres optimaux sont b =-1,15 et a =5,4 :

Dans le cas de la régression, il se trouve que des relations mathématiques relativement simples permettent de trouver d'emblée les paramètres qui minimisent la fonction d'erreur. Ainsi, la pente de la droite de régression en X est donnée directement par la formule suivante :
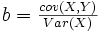
De la même façon, la pente de la droite de régression en Y est donnée par la formule
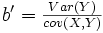
Les paramètres restants correspondent aux intercepts, c'est-à-dire à la valeur de Y quand X vaut 0 et à la valeur de X quand Y vaut 0. Sachant que les deux droites de régression passent par le centre de gravité G du nuage de points et que ce dernier a pour coordonnées
il est facile de dériver les intercepts.
Mais de toute façon, même si vous ne maîtrisez pas les mathématiques pour réaliser vous-mêmes ces calculs, pers logiciels le font très bien et de nos jours, on peut très bien faire des régressions sans réaliser un seul calcul soi-même. L'important est de comprendre la logique du processus. Un exemple de calcul détaillé sera présenté dans la rubrique "Zoom sur..."
Il reste maintenant à évaluer la qualité de l'ajustement produit. Cela est réalisé très simplement en calculant la corrélation entre les valeurs prédites par le modèle et les valeurs observées :
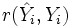
L'idée est que si la prédiction est parfaite, la corrélation sera de 1.
On peut alors montrer que la part de variance expliquée par le modèle est donnée directement par le carré de la corrélation précédente. Une valeur de r à 0.5 signifie alors que le modèle explique 0.5*0,5=25% de la variance.
10. Questionnaire d'auto-évaluation
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte