Échelles de mesure (Tout est-il mesurable ? )
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L1 |
| Livre: | Échelles de mesure (Tout est-il mesurable ? ) |
| Imprimé par: | Visiteur anonyme |
| Date: | jeudi 9 mai 2024, 19:53 |
Description
Objectifs : Définir le concept d'échelle de mesure et donner les éléments critiques nécessaires à son utilisation.
Prérequis :
- Application
- Loi normale
- Mesure, mesurage et codage numérique
- Relation d'équivalence
- Relation d'ordre et ordre partiel
- Relations entre Statistique et Psychométrie
Résumé : en Psychologie et plus généralement en Sciences Humaines et Sociales, les phénomènes auxquels on s'intéresse "n'émanent pas" de grandeurs mesurables, c'est-à-dire de grandeurs possédant des unités de mesure empiriquement définies. Les phénomènes se laissent plus naturellement décrire en termes de classifications et d'ordres partiels. Nombre d'applications psychologiques reposent sur des ordres considérés comme totaux, par approximation ou par convention, ainsi que sur la définition de distances conventionnelles relatives à des grandeurs hypothétiques. Ces trois approches, (i) classification, (ii) ordre total et (iii) distances, sont associées à ce que l'on appelle, après Stevens (1946), les échelles (i) nominale, (ii) ordinale et (iii) d'intervalle. Les échelles dites de ratio correspondent au mesurage au sens classique du terme. Une utilisation rigoureuse des échelles de mesure nécessite d'expliciter en quoi les codages associés à ces échelles représentent des opérations sur les objets faisant l'objet de l'échelonnement.
rédaction : Stéphane Vautier, 5 pages plus un test d'auto-évaluation final.
1. La représentation des relations empiriques entre objets
Dans son article intitulé « On the theory of scales of measurement » (De la théorie des échelles de mesure), Stevens (1946, p. 677) légitime l'usage des échelles de mesure par la référence à l'expérience :
"Scales are possible in the first place only because there is a certain isomorphism between what we can do with the aspects of objects and the properties of the numeral series. In dealing with the aspects of objects we invoke empirical operations for determining equality (classifying), for rank-ordering, and for determining when differences and when ratios between the aspects of objects are equal."
Stevens exclue que les échelles de mesure, destinées à échelonner des objets, puissent être utilisées de manière légitime s'il est impossible de faire référence à des opérations empiriques sur ces objets. Mais que signifie ici le terme "empirique", dès lors que les objets en question sont des comportements ou des énoncés ? On va voir que les opérations portant sur des "objets psychologiques" doivent être définies comme des opérations symboliques.
Remarque : les opérations "+" et "-" définies en mathématiques sont aussi des opérations symboliques.
2. Échelle nominale et classification
L'échelonnement des objets d'un ensemble E sur une échelle nominale repose sur l'établissement d'une relation d'équivalence sur les éléments de cet ensemble E. Autrement dit, pour tout couple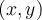 
d'éléments de E, il faut pouvoir décider si la proposition "
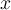est comme 
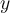" est vraie ou fausse. Ainsi, l'affirmation "
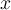" désigne le fait que appartient à la classe d'équivalence de .
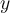Prenons comme exemple la réponse à un item de test : on considère l'ensemble des personnes à qui on soumet l'item, ainsi que l'ensemble des réponses apportées à l'item. On peut classer toute réponse selon son caractère correct ou non correct. Les réponses sont des objets empiriques en ce sens qu'on peut les observer et qu'on ne peut pas affirmer tout et n'importe quoi à leur sujet. La caractérisation des réponses du point de vue de leur caractère correct ou non correct repose sur la définition qu'on donne au terme "correct" (par exemple, "être identique à une réponse donnée"). Ainsi, on peut définir la relation d'équivalence "avoir la même réponse que" une fois que la réponse est caractérisée comme correcte ou incorrecte. On voit à travers cet exemple que le fait pour un répondant d'appartenir par sa réponse à la classe d'équivalence "correct" ou "incorrect" est le résultat d'un jugement fondé sur une définition. Ainsi, le fait d'appartenir à telle ou telle classe est un fait construit, par opposition à un fait qui s'imposerait de lui-même et en tant que tel à l'observateur.
Pour représenter l'ensemble des réponses du point de vue de cette caractérisation "correct/non correct", on peut utiliser les codes 0 pour "non correct" et 1 pour "correct". Par extension à l'ensemble des personnes, chaque personne sera ainsi échelonnée sur l'échelle (0, 1).
La classe de la personne (0 ou 1) permet de connaître le type de réponse qu'elle a fournie en traitant l'item du test, en référence à la convention qui fonde le référentiel de l'observation de la réponse à l'item.
3. Échelle ordinale et hiérarchisation
L'échelonnement des objets d'un ensemble E sur une échelle ordinale repose sur l'établissement d'une relation d'ordre, généralement réflexive, sur les objets (ou éléments) de cet ensemble. Autrement dit, pour tout couple 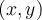d'éléments de E, il faut pouvoir décider si la proposition " 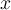est inférieur ou égal à 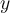"est vraie ou fausse.
Il est courant en Psychométrie d'ordonner les items d'un test selon ce que l'on appelle leur niveau de difficulté. Si tout item est caractérisé par son propre niveau de difficulté, il est le seul représentant de sa classe d'équivalence.
Le niveau de difficulté d'un item est défini relativement à une population de n répondants. Considérons que la réponse aux items est cotée 0 pour "incorrect" et 1 pour "correct". On peut affecter à chaque item le nombre de répondants ayant produit une réponse correcte. On peut ensuite comparer ces nombres à l'aide de la relation "est inférieur ou égal à", ce qui permet d'ordonner les items selon un critère "empirique" et, dirons-nous, de manière plus contemporaine, selon un critère opératoire bien défini. Il serait cependant naïf, et erroné, de considérer que la "difficulté" d'un item est une caractéristique inhérente à l'item, si on fait passer le test à une autre population de répondants, rien ne prouve que le niveau de difficulté des items demeurera identique à ce qu'il était relativement à une première population de répondants. Considérer qu'un item possède la propriété d'être plus ou moins difficile indépendamment d'une population de répondants est une forme de réification.
Un autre exemple d'échelle ordinale est fourni par les scores psychométriques composites. Cet exemple mérite qu'on y consacre une attention particulière, car il est implicitement admis, à tort, que les scores composites constituent un ordre total. Considérons un test composé de k items cotés 0 ou 1. On peut définir une relation d'ordre total sur les réponses de chaque item du test. En revanche, lorsqu'on considère l'ensemble des k-uplets de réponses au test, on ne peut définir qu'un ordre partiel.
Prenons un exemple concret pour illustrer ce point subtil.
Soit la réponse (0, 0, 1, 1) pour un test composé de quatre items ; soit pour le même test la réponse (0, 0, 0, 1) : dans ce cas, on a (0, 0, 0, 1) est inférieur ou égal à (0, 0, 1, 1), puisque :
- 0 est inférieur ou égal à 0,
- 0 est inférieur ou égal à 0,
- 0 est inférieur ou égal à 1,
- 1 est inférieur ou égal à 1.
Considérons maintenant les réponses (0, 0, 1, 1) et (1, 1, 0, 0). On a :
- 0 est inférieur ou égal à 1,
- 0 est inférieur ou égal à 1,
- 1 n'est pas inférieur ou égal à 0,
- 1 n'est pas inférieur ou égal à 0.
Les deux réponses ne sont pas comparables : (0, 0, 1, 1) n'est pas inférieur ou égal à (1, 1, 0, 0) d'une part et (1, 1, 0, 0) n'est pas inférieur ou égal à (0, 0, 1, 1) d'autre part. La relation "est inférieur ou égal à" est donc un ordre partiel sur l'ensemble de k-uplets de réponses, puisqu'il existe au moins deux éléments qui ne sont pas comparables.
En pratique, un ordre total est obtenu en remplaçant les réponses par la somme des codes qui caractérisent les réponses élémentaires. Il faut néanmoins remarquer que l'opération "+" sur des codes ordinaux n'est pas définie. C'est pourquoi les scores composites définissent un ordre total par convention. Cette convention repose sur le fait que les réponses dont les codes ont la même somme sont considérées comme appartenant à une classe d'équivalence, elle aussi conventionnelle. Le fait de considérer que les réponses que l'on regroupe dans une classe d'équivalence sont équivalentes peut être considéré comme une "approximation nominale".
Le programme de psychométrie de L3 présentera des modèles sophistiqués qui ont pour but de surmonter cette difficulté logique grâce à l'hypothèse que les items mesurent de manière probabiliste une unique grandeur psychologique. Le programme de psychométrie de L2 présentera des modèles plus faciles d'accès basés sur la même hypothèse.
4. Échelle d'intervalle et distances entre deux scores
Tandis que les données nominales ou ordinales sont des données qualitatives, les données échelonnées sur une échelle d'intervalle sont des données quantitatives (Stevens, 1946). Les scores sur une échelle d'intervalle permettent de déterminer la distance entre deux scores, qui représente une variation sur une grandeur. On peut alors définir une unité de mesure conventionnelle à laquelle on peut rapporter une variation définie expérimentalement. L'origine (le point zéro) d'une échelle d'intervalle ne représente rien de particulier par rapport à la grandeur sur laquelle on mesure les variations.
Par exemple, la distance entre le degré 20 et le degré 22 d'une échelle de température, qui correspond à la dilatation du mercure dans le thermomètre lorsque l'air ambiant passe d'un certain état thermodynamique à un autre, représente une variation de température (grandeur). Cette variation serait identique à la variation de température que représente la distance entre le degré 12 et le degré 14 de la même échelle et, plus généralement, à toute variation associée à une distance de deux degrés. Bien entendu, il faudrait pour être complet préciser comment on peut définir l'identité de deux variations, indépendamment des distances mesurées sur le thermomètre.
En Psychologie, les scores auxquels on attribue le statut de "mesures d'intervalles" ne correspondent pas nécessairement à des grandeurs expérimentales. Par exemple, les scores de QI, associés aux profils de performance observables avec ce que l'on appelle des tests d'intelligence, sont considérés comme des mesures d'intervalle par convention. Un argument parfois avancé est que ces scores se distribuent conformément à une loi normale lorsqu'on considère une large population de répondants. Certes, certaines grandeurs mesurables peuvent être associées à des distributions d'allure normale, comme la taille par exemple. Mais il est logiquement incorrect d'en déduire qu'un système de codage numérique pouvant être associé à une distribution d'allure normale est alors un système permettant de mesurer une grandeur, ou, en d'autres termes, une variable quantitative.
En pratique, on attribue le statut de mesure d'intervalle à des codes numériques dès qu'on applique à ces codes numériques les opérations algébriques +, -, x, /. Un exemple très répandu est celui qui consiste à traiter les notes scolaires comme des nombres.
5. Échelle de ratio ou proportionnelle
L'échelle de ratio, dite encore échelle proportionnelle, est fondée sur la possibilité de définir empiriquement des égalités de rapports ou de proportions. La mesure d'une grandeur est le nombre réel qui est égal au rapport de la grandeur sur la grandeur étalon. Les nombres permettant de compter des objets discrets sont définis sur une échelle de ratio.
Par exemple, supposons que lors d'une soirée télé-pizza, où des amis ont l'habitude de se partager par avance le contenu d'un sac de bonbons chocolatés de toutes sortes de couleurs, Brigitte reçoive 10 bonbons chocolatés, tandis que son ami Paul n'en obtienne que 5 ; supposons que Julie en ait reçu 12 tandis que son ami anglais Andrew doive se contenter de 6 bonbons. Peut-on affirmer que Brigitte a deux fois plus de bonbons que Paul ? (réponse : oui.)
Une telle affirmation n'a pas de sens si les scores sont au mieux échelonnés sur une échelle d'intervalle. Par exemple, supposons que lors d'une visite médicale, les températures mesurées à l'aide d'un thermomètre buccal se distribuent de la manière suivante :
- Brigitte 37,2 °C,
- Paul 37,0 °C,
- Julie 37,1 °C,
- Andrew 36,9 °C.
En soustrayant 37 à ces valeurs, on obtient une échelle d'intervalle, dont l'unité pourrait être appelée "degré prime" la distribution suivante :
- Brigitte 0,2 °',
- Paul 0,0 °',
- Julie 0,1 °',
- Andrew -0,1 °'.
En effet, les distances entre les "objets" sont bien respectées dans les deux échelles. Dans le contexte de ces mesures d'intervalle, affirmer que Julie a une température deux fois plus élevée que Brigitte n'a pas de sens. Une échelle permettant la comparaison de deux rapports ou proportions repose sur l'existence d'une origine absolue, l'absence de la grandeur mesurée.