Psychométrie

Par définition, une distribution normale est une distribution continue, ce qui n'est pas le cas des distributions de scores psychométriques ;on utilise néanmoins le modèle normal comme approximation pratique des distributions de scores psychométriques. On doit distinguer deux types de normes basées sur la distribution normale :

• les normes en scores,
• les normes en classes.

Les normes en scores

Les scores d'une distribution normale peuvent être interprétés à l'unité près. Par exemple, un score de QI est par définition un score appartement à une distribution normale de moyenne 100 et d'écart-type 15. Ainsi, un score de 115 se trouve à 1 écart type après la moyenne ; un score de 130 se trouve à 2 écarts-types après la moyenne.

Le modèle normal permet de connaître la probabilité d'un intervalle donné. Ainsi, on peut interpréter un score comme un événement plus ou moins rare en référence aux scores de la population de référence.

Si les scores composites d'un échantillon de référence suivent une distribution approximativement normale de moyenne m_d et d'écart type s_d, on peut calculer la valeur y d'un score brut x pour une norme de moyenne m_a et d'écart type s_a à l'aide de la formule suivante :

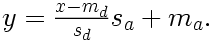
Les scores dans une distribution normale de moyenne 0 et d'écart type 1 sont des scores dits z. Les scores dans une distribution normale de moyenne 50 et d'écart type 10 sont des scores dits T.

Les normes en classes

On peut aussi "découper" une distribution normale en "tranches" verticales ordonnées. Chaque tranche est une classe ordonnée. Les classes dans un modèle de distribution en 9 classes sont appelées des stanines (Guillevic & Vautier, 2005).