Savoir trouver les valeurs critiques du t de student

Ayant procédé au test sous SPSS 18, notre chercheur obtient le tableau de résultats suivant :

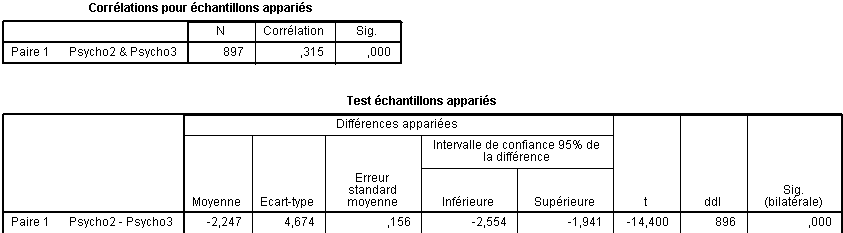
Tableau "Corrélations pour échantillons appariés"

 Ce tableau rapporte la corrélation qui existe entre les deux variables, ce qui est une donnée intéressante pour les calculs de tailles d'effet (qui ne sont pas dans ce cours) et qui renseigne aussi sur le degré de liaison entre les deux variables.

Ici le R de Pearson vaut 0,315 ce qui pour 897 couples de données est largement significatif ? Si l'on doit présenter cette corrélation dans le texte, on écrira " r (896)=.315, p <.001". Notez r (896) et non r (897), le nombre entre parenthèses représentant le nombre de degrés de liberté de la comparaison et non le nombre de couples.

Explication des colonnes de données du Tableau "Test échantillons appariés"

Moyenne : contient la moyenne des différences Psycho2-Psycho3, ici -2,247.

Ecart-type : Il s'agit de l'écart-type des différences Psycho2-Psycho3, ici 4,674.

Erreur standard moyenne : Ce nombre est utilisé pour calculer les intervalles de confiance ou pour des calculs intermédiaires. Il correspond à l'écart-type divisé par la racine carrée de N (donc ici 4,674 / racine(897) = 0,156. 

t : C'est tout simplement la valeur du t de student arrondie à la 3e décimale, obtenue en comparant les deux moyennes précédentes soit t =-14,400. Le signe "-" vient de ce que la différence (m_1- m₂) est négative. 

ddl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons indépendants, le nombre de sujets moins 1, soit 896.

Sig. (bilatérale) : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, tronquée à la troisième décimale, soit 0,000. Comme cette valeur est inférieure au seuil de 5%, soit 0,05, on considérera le test comme significatif et on peut donc dire que les notes Psycho3 sont significativement supérieures aux notes Psycho2.

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans un texte qui suit les normes APA 7^e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des résultats à l'épreuve Psycho2 est M₂ =11.50 (SD = 4.33) alors que celle des femmes est M₃ =13.75 (SD = 3.59). La moyenne des notes à Psycho3 est significativement plus forte t(896) = 14.44, p <.001".

En fait, on doit écrire p<.001 car, si l'on regarde la valeur du p calculé avec plus de décimales (ce qui n'apparaît pas sur l'image ci-dessus), on constate que la valeur de p est extrêmement proche de 0, et en tout cas inférieure à .001.