Psychologie, statistique et psychométrie
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L1 |
| Livre: | Psychologie, statistique et psychométrie |
| Imprimé par: | Visiteur anonyme |
| Date: | samedi 21 février 2026, 23:10 |
Description
 Cette première grande leçon introduit la psychométrie et la statistique dans la perspective historique du développement de la psychologie scientifique à partir du XIX
e
siècle, afin de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques, et techniques de ces matières. Ces enjeux comprennent en particulier l'établissement de grandeurs mesurables et la mise au point de méthodes objectives pour l'étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette première grande leçon introduit la psychométrie et la statistique dans la perspective historique du développement de la psychologie scientifique à partir du XIX
e
siècle, afin de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques, et techniques de ces matières. Ces enjeux comprennent en particulier l'établissement de grandeurs mesurables et la mise au point de méthodes objectives pour l'étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Rédaction : Éric Raufaste, Stéphane Vautier
Table des matières
- 1. La science comme dialogue avec le réel
- 2. Variabilité et invariants en psychologie
- 3. Dimensions de la variabilité en psychologie
- 4. Variabilité due à l'erreur
- 5. Quantification de la variabilité
- 6. Variabilité et distributions
- 7. Relations entre Statistique et Psychométrie
- 8. Questionnaire d'auto-évaluation
1. La science comme dialogue avec le réel
Objectifs. Mettre en perspective l'activité de recherche scientifique en général, et psychologique en particulier.
Prérequis. Aucun.
Résumé. Faire de la science, c'est chercher à décrire une réalité objective. Dans l'histoire de cette recherche d'objectivité, deux grandes approches se sont toujours affrontées : une approche descendante (dite « hypothético-déductive ») où les modèles sont issus de la raison de l'homme, et une approche ascendante (dite « inductive) où le chercheur observe d'abord la réalité empirique puis en propose une description. Les progrès de l'épistémologie nous montrent qu'il faut renoncer à l'idée de connaissance absolue pour les sciences empiriques comme la psychologie. En tant que science empirique, la psychologie doit donc se doter d'outils permettant de fournir les descriptions les moins entachées d'erreur.
1.1. Monde empirique et monde des idées
La construction de la connaissance scientifique peut se concevoir comme la production d'un discours par une suite d'allers-retours entre le monde de la réalité empirique et le monde des croyances. Dans le schéma suivant, l'ellipse du haut représente le monde des idées ou des croyances, et celle du bas représente le monde des phénomènes empiriques.
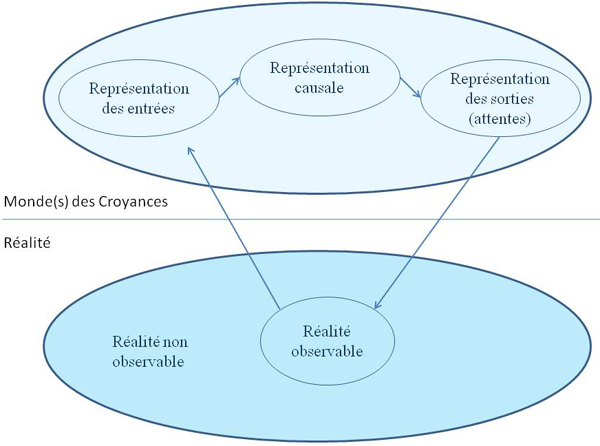
En considérant l'ellipse de la réalité empirique, on peut distinguer deux régions.
- La première est celle de la réalité observable, à partir de notre activité perceptive et interprétative, comme des comportements, par des appareils de mesure, ou diverses techniques d'observation (un test de personnalité par exemple).
- La plus grande partie (et le dessin ne fait pas justice de l'infinie disproportion entre ces deux parties) représente cette partie de la réalité qui n'a jamais été observée et qui ne le sera jamais.
En considérant l'ellipse du monde des croyances, on peut distinguer trois régions intéressantes.
- La première est celle qualifiée ici de représentation des entrées. En effet, lorsque nous observons la réalité, nous en donnons une description, et c'est en réalité cette description, et non la sensation elle-même, qui entre dans la suite de nos raisonnements. Par exemple, si mes yeux captent l'image d'une magnifique plage ensoleillée dans une île du pacifique, ce qui va entrer dans ma mémoire, ce que je raconterai à mes amis, le souvenir sur lequel je baserai mes décisions futures, tout cela n'est qu'une description très simplifiée de la sensation initiale.
- La deuxième région est celle de la représentation causale. Par exemple, je peux attribuer l'origine du plaisir que j'ai ressenti à ce moment à la magie du lieu, ou encore aux relations humaines très riches dont j'ai fait l'expérience ce jour là.
- La troisième partie concerne ici les prédictions que je peux faire à partir de mon modèle causal. Par exemple, si je crois que l'origine de la sensation de plaisir que j'ai ressentie sur cette plage est liée aux couleurs très particulières ce jour là, il est probable qu'à l'avenir je rechercherai à faire d'autres expériences d'endroits aux couleurs magiques. Si par contre, je crois que la cause de mon plaisir était avant tout la compagnie des amis qui étaient avec moi à ce moment là, ce que je rechercherai probablement à l'avenir ce sont des situations où de telles relations humaines seront possibles.
On voit que les prédictions issues du modèle causal vont déterminer mes comportements d'observation et d'exploration de la réalité, et donc mes expériences futures de la réalité. Ces dernières conditionnent par ailleurs l'apparition de nouvelles croyances, etc. La connaissance scientifique se construit donc comme une suite d'aller-retours entre le monde des croyances et le monde empirique : Les observations du monde empirique fournissent la matière à des descriptions et des explications, qui vont conduire à de nouvelles croyances déduites (les prédictions), qui vont secondairement guider de nouvelles observations dans le monde empirique, etc.
Jusqu'ici, nous avons évoqué des relations entre le monde empirique et les croyances. Mais que deviennent les connaissances dans tout ça ? Nous allons le voir page suivante...
1.2. La science construit-elle des connaissances ou des croyances ?
Dans la page précédente, nous avons évoqué des allers-retours entre le monde empirique et le monde des croyances. Mais ces idées sont-elles des croyances ou des connaissances ? A priori, la science s'intéresse seulement à ces dernières et ne considère les premières que comme objets d'études pour le psychologue, le sociologue ou l'anthropologue. Mais est-ce satisfaisant ?
Les traditions rationaliste et empiriste
Considérons cette première citation :
« Connaître et connaissance désignent donc un genre dont les espèces sont constater, comprendre, percevoir, concevoir, etc. Ils s'opposent à croire etcroyance, non par la force de l'adhésion, mais par le fait que ces deux derniers termes n'impliquent pas nécessairement l'idée de vérité. »
Une vieille tradition distingue ainsi d'un côté les « croyances », supposées peu crédibles, et en tout cas non partagées par tous les individus, et les « connaissances », apanage des esprits éclairés et traduisant la vérité de l'état du monde. Dans une telle conception, le progrès de la science consiste essentiellement à acquérir de plus en plus de connaissances et à se débarrasser des croyances, ces dernières étant d'ailleurs souvent affublées de l'épithète « fausses » pour le cas où l'on ne réaliserait pas le fossé fondamental qui les sépare des connaissances.
Si ces positions, maintenant dépassées, ont pu à la rigueur sembler tenables dans le domaine des sciences exactes, il devient plus difficile de s'y tenir dès qu'on aborde le cas des sciences empiriques, dont fait partie la psychologie. Ces dernières, jusques et y compris la physique, partagent le présupposé d'une réalité externe au langage qu'elles utilisent pour la décrire (réalité que nous avons appelée ici, monde empirique).
Le falsificationisme
« Une théorie qui n'est réfutable par aucun événement qui se puisse concevoir est dépourvue de caractère scientifique. »
Karl Popper, Conjectures et réfutations, ch.1, section 1.
Nous sommes là confrontés à une conception radicalement différente. Une connaissance n'est cette fois-ci qu'une croyance temporairement acceptée jusqu'à ce que, tôt ou tard, une nouvelle théorie vienne déchoir l'ancienne. Certes, certaines croyances peuvent ainsi prendre temporairement le statut de « connaissances », lorsque suffisamment d'individus avec un statut social suffisamment élevé décident ensemble que ces croyances sont de bons modèles de la réalité empirique. Mais l'expérience montre que, quelques siècles plus tard, ces connaissances pourront redevenir de simples croyances, remplacées par d'autres systèmes de croyances (par exemple, il a longtemps été admis comme connaissance vraie, l'idée que la terre... était plate).
Comment résoudre cette opposition fondamentale ? En fait, tout s'éclaire si l'on distingue deux domaines de réalités, le monde de la réalité empirique et le monde des idées (à la Platon). Dans le monde de la raison (et donc du courant épistémologique appelé « rationalisme »), celui des sciences dites exactes (mathématique, logique), les vérités sont éternelles. À l'intérieur d'un système d'axiomes donnés (par exemple ceux de la théorie des ensembles), les conclusions logiques qu'on peut dériver resteront vraies encore dans un million d'années (un plus un feront toujours deux). On peut certes changer les axiomes, ce qui changera les conclusions, mais chaque système axiomes-conclusions restera inchangé.
Regardons maintenant le monde de la réalité dite objective, celui du monde quotidien dans sa presque infinie complexité. Il est clair qu'on peut dériver des lois mathématiques qui décrivent assez bien certaines réalités, comme n'importe quel lycéen l'a appris en cours de physique. Il reste que si l'on observe la réalité avec suffisamment de détails, cette réalité finira tôt ou tard par s'écarter de la prédiction du modèle théorique. On pourra alors rejeter le modèle théorique ou au moins en réduire la portée. De plus, même si l'on a observé 10 millions de fois le même comportement de la réalité, comment peut-on être sûr que lors de la 10 millions unième fois, la réalité ne va pas changer de comportement ? Notre certitude, étayée par la répétition d'expériences semblables, ne repose donc que sur un acte de foi : ce qui a toujours été observé dans le passé va se maintenir dans le futur !
Un autre problème important est que, même si l'on se cantonne à la réalité actuelle, on ne peut pas tout observer, ne serait-ce que par ce qu'il y a trop d'humains. Pire, il existe une part d'indétermination intrinsèque dans la réalité empirique. On va donc devoir développer des connaissances intrinsèquement associées à une part d'ignorance. Le lecteur intéressé par l'histoire des statistiques et l'épistémologie trouvera des compléments sur cette question dans le « zoom sur » consacré aux relations entre l'incertitude et la connaissance.
Pour en revenir à la question qui nous occupe ici, « nos connaissances du monde sont-elles vraiment plus que des croyances ? », il résulte de ce qui précède que les connaissances doivent être avant tout conçues comme des croyances provisoirement tenues pour vraies. Cette position est évidemment dérangeante, car elle nous impose de renoncer au confort que constitue la possession de certitudes.
Un arsenal méthodologique
Tout est-il donc perdu ? Est-ce à dire que les connaissances scientifiques ne vaudraient pas mieux que les prédictions des astrologues ? Pourtant, la science a maintes fois prouvé qu’elle pouvait développer des connaissances utilisables pour prédire et contrôler le réel. Donc, même si de telles connaissances sont amenées ultérieurement à être révisées, elles capturent nécessairement quelque chose de la réalité.
Une fois admis qu'il n'y a de réalité empirique que relative, il reste donc encore plusieurs moyens d'améliorer les chances que nos constructions théoriques, nos modèles de la réalité, résisteront au temps. Ces moyens consistent précisément
- à améliorer les outils de mesure et techniques d'observation afin de renforcer la crédibilité et la validité des faits d'observation,
- à déployer un arsenal méthodologique visant à améliorer le processus d'induction (la construction de modèles à partir des observations). Arsenal au sein duquel figurent en bonne place l'emploi de statistiques et, pour la psychologie plus spécifiquement, l'emploi des méthodes développées en psychométrie.
Ainsi les connaissances scientifiques sont-elles produites selon une méthodologie qui, sans garantir la réalité des résultats obtenus, et eu égard aux possibilités techniques d'une époque donnée, représente néanmoins la meilleure façon de produire des connaissances probablement justes : Ce qui caractérise les connaissances scientifiques, ce n’est pas que l’on peut dire avec certitude qu’elles sont justes, c’est qu’elles ont été produites selon une démarche, la démarche scientifique, qui maximise leur probabilité d’être juste, compte tenu de l’état de l’art au moment de leur production.
Dans l'article suivant, nous verrons que cet arsenal s'articule autour d'une idée forte : la recherche d'invariants et l'analyse de la variabilité dans les phénomènes étudiés.
2. Variabilité et invariants en psychologie
Objectifs. Introduire les notions de variabilités inter-individuelle et intraindividuelle.
Prérequis. Leçon : la science comme dialogue avec le réel.
Résumé. La science est fondamentalement une recherche d'invariants. Cette recherche passe par l'analyse de la variabilité des phénomènes étudiés pour en inférer la structure sous-jacente (induction) ou pour tester les prédictions des théories imaginées pour rendre compte de ces phénomènes.
Dans l'article précédent, nous avons vu que la science procède par aller-retour entre observations du monde empirique et construction de systèmes descriptifs et explicatifs dans le monde des croyances. Nous allons maintenant développer deux notions complémentaires qui permettent de joindre ces deux ordres de réalités.
1. Notion générale d'invariant
 |
(…) la stratégie fondamentale de la science dans l'analyse des phénomènes est la découverte des invariants. Toute loi physique, comme d'ailleurs tout développement mathématique, spécifie une relation d'invariance... Jacques Monod (1970, p. 134). Le Hasard et la Nécessité |
|---|
Il peut y avoir des motivations très différentes pour inciter un chercheur à produire des connaissances. Une première motivation est la pure curiosité intellectuelle, l'envie de comprendre comment les choses marchent en général. Une autre motivation est l'envie de mieux maîtriser le monde. En effet, si l'on comprend comment les choses marchent, alors on peut plus facilement se placer en position de les contrôler. Ce qu'on appelle usuellement « recherche fondamentale » est ainsi la production de croyances censées s'appliquer à de multiples situations plus ou moins différentes des situations où ont été faites les observations qui ont conduit à produire ces connaissances. On considère qu'on a appris quelque chose si la croyance que l'on a produite à partir d'une observation trouve à s'appliquer pour expliquer ou prédire de nouvelles situations. Il faut donc bien qu'il y ait un point commun à ces différentes situations et que ce point commun soit décrit de façon satisfaisante par le système de croyances que l'on a adopté pour en rendre compte. Un tel point commun est ce qu'on appelle un invariant.
Le lecteur devrait pouvoir reconnaître sans problème que l'essentiel des connaissances fondamentales sur le monde empirique est constitué de descriptions dites générales précisément parce qu'elles décrivent quelque chose d'invariant.
2. Relations entre invariants et déterminismes
Le problème immédiat lorsque l'on considère les phénomènes psychologiques tient précisément à l'incroyable diversité des formes que peuvent revêtir nos comportements et à leur caractère finalement assez peu prédictibles. Historiquement, les invariants psychologiques ont été recherchés à partir de deux types de déterminants complémentaires : les déterminations biologiques et sociales. En effet, plus les phénomènes que l'on étudie sont proches du niveau biologique, et plus les déterminations biologiques contraignent la diversité. Le comportement de l'embryon est très prévisible, car très déterminé biologiquement. Pour ne prendre qu'un exemple, les humains peuvent percevoir les sons dans une bande de 20 à 20000 Hz. Les individus capables de percevoir les ultra-sons au-delà de 20000 Hz sont très rares, d'autant plus rares que la fréquence considérée est supérieure à 20000 Hz. D'un autre côté, société et culture contraignent, elles aussi, les comportements. Ainsi, un individu né en France et élevé en France aura une très forte probabilité de parler français plutôt qu'une autre des milliers de langues actuellement présentes dans le monde.
Si la diversité des contraintes auxquelles est soumis un individu finit par imposer certains invariants dans les comportements, il reste que chaque sujet humain possède une part de liberté qui rend son comportement non totalement prévisible. La psychologie en tant que science descriptive peut précisément être considérée comme la recherche des invariants du comportement humain qui ne se laissent réduire ni au niveau biologique ni au niveau social. En tant que science explicative, il s'agit de la recherche des mécanismes psychologiques qui causent ces invariants comportementaux. La psychologie en tant que science descriptive peut précisément être considérée comme la recherche des invariants du comportement humain qui ne se laissent réduire ni au niveau biologique ni au niveau social
La démarche scientifique vise l'objectivité. Le propre de l'objectivité, c'est la possible mise en commun entre plusieurs individus d'une réalité qui existe en dehors de chacun d'eux. Ainsi, une croyance aura d'autant plus tendance à être considérée comme une connaissance au sens fort (une « croyance vraie », si l'on préfère) si tous les individus qui la considèrent s'accordent sur sa validité. Ce critère se retrouve sous une autre forme bien connue : la nécessaire réplicabilité des expériences, c'est-à-dire le fait qu'une expérience scientifique devrait produire les mêmes résultats quelle que soit la personne qui réalise l'expérience. Ainsi, la science en général s'applique à elle-même un critère d'invariance relativement à la transformation qui consiste à passer d'un individu expérimentateur à un autre.
3. Dimensions de la variabilité en psychologie
Objectifs. Introduire les principaux angles sous lesquels la variabilité psychologique peut être analysée.
Prérequis. Leçon : variabilité et invariants en psychologie.
Résumé. La psychologie est une science du sujet, animal ou humain. Elle s'applique donc à la fois à des données observables et à des données subjectives. La variabilité psychologique peut aussi s'analyser en termes des invariants au sein d'une population, de variabilité entre sous-populations avec invariance dans chaque sous-population, ou directement au niveau de la variabilité pour un même individu. L'analyse de la variabilité en psychologie impose donc de distinguer les notions de variabilité inter-individuelles et intraindividuelles. Enfin, la variabilité en psychologie, comme dans toute autre science résulte à la fois de mécanismes systématiques et d'effets aléatoires.
3.1. Subjectivité et objectivité
Dans l'article précédent, nous avons introduit les notions de variabilité et d'invariants. Nous allons maintenant nous interroger sur les dimensions de la variabilité en psychologie, c'est-à-dire identifier des façons différentes et indépendantes d'aborder cette variabilité. Nous considérerons en particulier deux dimensions : le couple phénomènes subjectifs/ phénomènes objectifs et la distinction entre les phénomènes intra et interindividuels.
(…) nous saisissons dans notre perception, tout à la fois, un état de notre conscience et une réalité indépendante de nous.
H.Bergson, Matière et Mémoire (1999,p.229).
Traditionnellement, en psychologie, les phénomènes auxquels on s'intéresse sont de deux ordres très différents, qui impliquent chacun leur méthode privilégiée d'investigation : les données observables, et les données subjectives.
Les données observables

Le premier ordre de phénomènes concerne les éléments « directement observables par le chercheur (éventuellement au travers d'un instrument ou d'une grille d'analyse). Il peut s'agir de comportements, mais aussi de manifestations physiologiques plus ou moins faciles d'accès comme les mouvements oculaires (l'enregistrement des endroits regardés par l'œil en temps réel), l'électroencéphalogramme, l'enregistrement des variations électriques à la surface de la peau, la consommation d'oxygène dans le cerveau, les temps de réponse, etc. Ces indices nous renseignent de façon assez objective sur les processus psychologiques en train de se dérouler (bien que de la subjectivité puisse déjà se nicher dans le choix des éléments observés ou dans la construction des grilles d'analyse). Se pose cependant le problème de la signification qu'il faut leur donner.
Par exemple, si l'on observe que les mains d'un garçon deviennent moites chaque fois qu'il est mis en présence d'une fille particulière, on est sûr que cette fille le fait réagir. Mais quelle signification psychologique donner à cette réaction : Est-ce du désir ? Ou bien qu'elle lui rappelle quelqu'un qu'il a connu et dont il n'a pas encore intégré la perte ? Ou bien refoule-t-il une homosexualité qu'il n'assume pas ? Ou mille autres explications dont la variété n'est limitée que par l'imagination de l'observateur.
Les données subjectives

Le second grand ordre de phénomènes qui nous occupe en psychologie concerne les contenus de conscience, à savoir les impressions subjectives ressenties par les sujets et rapportées au chercheur au travers du langage. Par exemple, supposons que je veuille évaluer le degré de confort ressenti par un consommateur qui essaie une voiture. Ou encore le niveau d'angoisse qu'il ressent en général. Ou encore la confiance qu'il ressent en l'avenir. Ces choses sont accessibles à la conscience du sujet, mais ne le sont pas (en tout cas pas encore) à l'investigation technologique indépendante des verbalisations. Bien que largement discréditées au début du XX siècle avec l'apparition du behaviorisme, suite à l'échec des travaux fondés sur l'introspection, les mesures subjectives sont aujourd'hui de plus en plus utilisées, même si cela s'accompagne normalement d'un luxe de précautions méthodologiques pour minimiser les risques d'obtenir des données sans réelle fiabilité. Elles ont en effet un intérêt appliqué pour remplir divers objectifs au rang desquels figure, par exemple, la construction de situations de travail plus ergonomiques, moins pénibles, sollicitant moins les ressources des individus placées dedans.
siècle avec l'apparition du behaviorisme, suite à l'échec des travaux fondés sur l'introspection, les mesures subjectives sont aujourd'hui de plus en plus utilisées, même si cela s'accompagne normalement d'un luxe de précautions méthodologiques pour minimiser les risques d'obtenir des données sans réelle fiabilité. Elles ont en effet un intérêt appliqué pour remplir divers objectifs au rang desquels figure, par exemple, la construction de situations de travail plus ergonomiques, moins pénibles, sollicitant moins les ressources des individus placées dedans.
Ici, la psychologie se démarque fondamentalement des sciences qui visent l'objectivité complète (dans l'objet étudié comme dans la description qui en est donnée). Depuis la fin du behaviorisme, dans les années 1950, on considère que la psychologie doit aussi s'intéresser aux contenus des expériences subjectives, visant en quelque sorte à objectiver ce qu'il peut y avoir d'invariant dans les expériences subjectives.
Remarque importante
Le lecteur attentif aura pu remarquer que nous n'avons pas fait le choix d'opposer aux données subjectives les données « objectives », mais les données « observables ». Ce choix repose sur deux raisons principales.
- La première tient à ce qu'on sait maintenant que des expériences subjectives peuvent parfois être au moins partiellement objectives au sens scientifique. L'expérience de la douleur par exemple, a des corrélats physiologiques. Il s'ensuit que la notion de subjectivité ne s'oppose pas nécessairement à l'objectivité scientifique.
- La seconde raison, complémentaire, tient à ce que le caractère observable d'une donnée ne garantit pas non plus son objectivité au sens scientifique. Ainsi, il est possible d'avoir des biais systématiques dans le système de mesure, lequel repose d'ailleurs sur des présupposés théoriques dont on s'aperçoit parfois ensuite qu'ils étaient contestables.
3.2. Variabilités intra et interindividuelle
Variabilité et invariants intra individuels

Le propre du subjectif, de l'expérience vécue à un niveau phénoménologique, est précisément de ne pas prendre pour référence ce qui est en dehors du sujet. L'expérience subjective que j'ai du goût du miel m'appartient et absolument rien ne garantit que mon expérience subjective d'une situation est identique à celle de mon voisin placé dans la même situation. Bien au contraire, on a de bonnes raisons de penser que dans de nombreux cas, l'expérience que je fais en tant qu'individu situé dans le monde est absolument unique. Du de fait, les variations dans mon expérience unique ne peuvent s'aborder que par rapport à moi-même, sous un angle intraindividuel.
Bien entendu, je peux aussi être amené à faire l'expérience un grand nombre de fois d'un même type de situations et dégager des invariants de cette série d'observations. Par exemple, à chaque fois que je mange des marrons glacés, je ressens un vif plaisir. Donc pour moi, la relation « marrons glacés - plaisir » est un invariant.
En restant au niveau d'un seul individu, le niveau intraindividuel, je peux donc observer de la variabilité et décrire des invariants. La simulation qui suit illustre ce que représente une série de mesures intraindividuelles. Dans cette simulation, à chaque fois que vous cliquez sur le bouton « Donner une note », le programme va simuler une nouvelle mesure intraindividuelle de performance à un test. Vous pourrez utiliser l'ascenseur pour visualiser l'ensemble de la série de mesures intraindividuelles.
Ainsi pour chaque expérience particulière je peux dégager une part générale, commune avec d'autres expériences que j'ai fait dans le même type de situations, et une part totalement unique, absolument imprévisible et qui ne sera jamais répétée.
Que se passe-t-il maintenant si j'observe non pas un seul, mais plusieurs individus ?
Variabilité et invariants interindividuels
 Nous considérons maintenant une population d'individus et non plus un individu unique. Certains phénomènes seront de portée entièrement générale, concernant tous les individus sans exception1, tandis que d'autres phénomènes seront entièrement individuels, « idiosyncrasiques », traduisant une variabilité maximale. Entre ces deux extrêmes, il y a place pour des niveaux intermédiaires, correspondant à des phénomènes invariants au sein d'une sous-population, mais qui varient entre différentes sous-populations (par exemple, au sein des humains, nous allons distinguer les hommes et les femmes, ou encore les optimistes et les pessimistes).
Nous considérons maintenant une population d'individus et non plus un individu unique. Certains phénomènes seront de portée entièrement générale, concernant tous les individus sans exception1, tandis que d'autres phénomènes seront entièrement individuels, « idiosyncrasiques », traduisant une variabilité maximale. Entre ces deux extrêmes, il y a place pour des niveaux intermédiaires, correspondant à des phénomènes invariants au sein d'une sous-population, mais qui varient entre différentes sous-populations (par exemple, au sein des humains, nous allons distinguer les hommes et les femmes, ou encore les optimistes et les pessimistes).
La simulation qui suit illustre ce que représente une série de mesures interindividuelles. On imagine ici qu'un échantillon d'individus a été tiré au hasard au sein de la population française, et que chaque individu de l'échantillon fait l'objet d'une mesure de sa taille. En cliquant sur « Mesurer une personne », une nouvelle mesure interindividuelle est ajoutée à la liste.
Pourquoi distinguer variabilité intra- et interindividuelle ?
L'étude des variations intra-individuelles nous renseigne sur ce qui se passe pour de vrais individus, des individus qui existent réellement, tandis que les variations interindividuelles ne nous renseignent que sur une abstraction, à savoir la population étudiée. Toutefois, les variations intra-individuelles ne sont pas toujours possibles à étudier, car il n'y a pas d'indépendance des mesures intraindividuelles entre elles. Le fait que j'ai mesuré l'individu X au temps t est connu de cet individu et sa réponse au temps t +1 peut-être affectée par sa réponse au temps t (par exemple il veut paraître cohérent entre ses réponses).
Cette absence d'indépendance peut poser des problèmes expérimentaux mais, même en restant à un niveau purement statistique, elle implique que certains traitements mathématiques deviennent illégitimes. Vous verrez au cours des différents cours de statistiques dont vous bénéficierez dans vos études que les procédures à employer sont souvent sensiblement différentes selon le type de variabilité à traiter.
3.3. Variations aléatoires et variations systématiques
Le lecteur intéressé par ces notions et par l'histoire des sciences trouvera un complément d'informations dans l'article sur les relations entre les concepts de connaissance et incertitude.
Variations systématiques

Ce sont les variations du phénomène observé qui résultent d’un mécanisme déterministe. Par exemple, si l’on met en relation les variations de performances scolaires d’élèves avec les variations dans leur niveau d'effort, on pourra observer que souvent les élèves qui travaillent obtiennent des meilleures notes que les élèves qui ne travaillent pas. Ainsi, on pourra dire que l’effort est un déterminant de la réussite scolaire. Ce n’est évidemment pas le seul, mais une part des variations de réussite scolaire est donc explicable par les variations d’effort.
Il faut distinguer deux classes de variations systématiques : celles qui sont réellement liées à notre hypothèse causale, et celles qui sont en réalité dues à des biais méthodologiques. Par exemple, si pour tester l'hypothèse précédente, on compare des enfants qui avaient travaillé beaucoup à des enfants ayant moins travaillé, mais sans s'apercevoir que ceux qui travaillaient beaucoup étaient aussi issus de milieux culturellement plus favorisés, il s’agit bien d’une variation systématique, mais par rapport à l'hypothèse à tester, on parlera plutôt d’un biais en faveur de ces enfants. Une part importante de la réflexion scientifique et de la démarche de création de connaissances en psychologie expérimentale consiste précisément à vérifier que les résultats obtenus ne sont pas le fruit de biais systématiques.
Variations aléatoires

L’aléa est généralement invoqué dans une situation où des variations sont observables sans qu’absolument aucun déterminant ne permette de prédire dans quelle direction se fera la variation. Ou même, de façon plus radicale, sans qu’aucune détermination d’aucune sorte soit à l’œuvre (par exemple dans certains phénomènes quantiques, en physique). Ou encore, quand des variations sont dues à des déterminismes tellement faibles qu’il serait quasiment impossible de les repérer ou même de prédire la variation qu’ils vont induire lors d’une observation donnée. Le résultat serait encore perçu comme le «fruit du hasard».Les variations aléatoires correspondent donc à des variations sans déterminant connaissable.
On peut ranger dans cette catégorie un nombre d'erreurs directement liées à l'imprécision des instruments de mesure.
Une conséquence très importante de l'existence des erreurs aléatoires est que lorsque l'on procède à des séries de mesures physiques, il faut s'attendre dans le cas à général à trouver de la variabilité par le simple fait que des fluctuations aléatoires vont perturber les résultats. Ainsi plusieurs mesures du même objet vont donner des valeurs légèrement différentes. Dans le cas de mesures psychologiques, il en va de même.
De l'utilité de distinguer ces deux types de variations

Imaginons une recherche empirique dans laquelle le chercheur souhaite tester une hypothèse causale, disons comme celle vue précédemment, « l’effort favorise la réussite scolaire ». Il va donc devoir mettre en relation les variations de la variable qu’il postule comme étant la cause (l'effort), et les variations de la variable qu’il postule comme étant l’effet (la réussite scolaire). Grâce à des méthodes statistiques sur lesquelles nous reviendrons plus loin dans ce cours, il va donc pouvoir distinguer au sein des variations de la variable à expliquer...
- une part de variations systématiques « vraies » attribuable aux variations de la variable explicative,
- une part de variations systématiques attribuables à des biais (aussi appelée « erreurs systématiques » et,
- une part de variations aléatoires (aussi appelées « erreurs fortuites » ou « bruit »).
Le chercheur pourra alors dire qu’on connaît d’autant mieux le phénomène que sera importante la part des variations systématiques vraies, c’est-à-dire les variations attendues, celles dont il avait fait l’hypothèse, au sein de l’ensemble de toutes les variations. C’est ce concept qu’exprime la notion fréquemment employée de « part de variance expliquée ».
Le point intéressant est qu'une analyse mathématique des variations aléatoires a permis de repérer certaines propriétés dont la plus connue est sans nul doute que ces variations se laissent souvent décrire par la loi normale, fameuse courbe en cloche dite « courbe de Gauss » (à tort, Laplace par exemple ayant décrit cette distribution avant Gauss). Ces propriétés étant connues, on peut alors analyser les variations observées pour voir si elles se différencient du hasard ou non. La part de variations qui ne s’explique pas par le hasard peut alors être attribuée à des effets systématiques.
4. Variabilité due à l'erreur
Objectif. Introduire la notion d'erreur sous différentes formes (erreur de mesure, fonction d'erreur, erreur statistique).
Prérequis. Leçon : Dimensions de la variabilité en psychologie.
Résumé.
La notion d'erreur dans les mesures vient de la physique où elle était initialement conçue comme l'écart entre une valeur vraie et une valeur observée. La notion de fonction d'erreur a été introduite au XIX siècle par Laplace pour rendre compte des petits écarts constatés entre les prédictions des meilleurs modèles mathématiques et les observations de la réalité empirique que les modèles mathématiques étaient censés prédire.
siècle par Laplace pour rendre compte des petits écarts constatés entre les prédictions des meilleurs modèles mathématiques et les observations de la réalité empirique que les modèles mathématiques étaient censés prédire.
1. Notion d'erreur de mesure

Initialement, les physiciens ont cherché à mesurer diverses grandeurs, comme par exemple la taille d'un objet, la durée d'un moment, le périmètre de la terre, etc. Or, ils se sont rapidement aperçus que si l'on répète plusieurs fois la mesure d'un même objet, on a tendance à trouver des résultats légèrement différents. Pour expliquer ces résultats, une idée naturelle consiste à considérer qu'il existe une valeur vraie de la mesure, mais que le processus de mesure étant entaché d'une multitude d'erreurs, plus ou moins grosses, la valeur observée est différente de la valeur vraie. On appelle alors erreur l'écart entre la valeur observée et la valeur vraie :
À partir de là, le problème devient de séparer ce qui est la valeur vraie, celle que l'on recherche, de l'erreur. Séparer le bon grain de l'ivraie en quelque sorte.
Une première méthode pour cela, consiste à répéter les mesures de l'objet un grand nombre de fois. On peut alors espérer qu'en faisant la moyenne de toutes ces mesures, le résultat obtenu fournira une estimation à peu près correcte de la valeur vraie. Mais nous verrons plus loin que l'idée de multiplier le nombre de mesures de l'objet et d'en faire la moyenne ne met pas le chercheur à l'abri de différents biais.
2. Notion de fonction d'erreur
Le concept d'une fonction d'erreur a été introduit par le physicien français Pierre-Simon de Laplace.
Ce dernier était tenant d'une position déterministe très ferme, au point qu'il avait imaginé la notion d'un démon qui serait capable, ayant connaissance de toutes les positions et vitesses initiales de toutes les particules de l'univers, de pouvoir prédire tout état futur de l'univers. Laplace s'est notamment illustré pour avoir appliqué la mécanique newtonnienne au fonctionnement du système solaire avec un succès qui impressionna ses contemporains et établit le modèle d'un monde céleste réglé avec la précision d'une horloge. Après Laplace, et jusqu'à une période relativement récente, on considèrera que l'univers est entièrement prévisible.

Bien sûr, Laplace constate ça et là de petits désaccords entre les modèles mathématiques qu'il a déduits de la théorie newtonnienne et les données d'observations de la mécanique céleste. Pour traiter cette question, il introduit alors la notion de fonction d'erreur qui nous occupe ici. Cette dernière est un terme qui regroupe une multitude de choses qui, pour faire court, se résument à l'ensemble des sources de variations qui ne font pas partie du modèle mathématique du phénomène étudié lui-même.
Par exemple, si le chercheur essaie de prédire la position future d'une planète d'après les observations actuellement disponibles, il dispose d'un modèle mathématique du déplacement des planètes. En appliquant les équations de son modèle aux données d'observations, il va ainsi produire une position prédite. Même en supposant le modèle juste, si l'on regarde la position réelle de la planète dans le ciel au moment attendu, il y aura généralement de petites différences. Par exemple à cause de petites variations dans l'atmosphère terrestre qui faussent les images, ou encore d'erreurs de notations de l'observateur. L'écart entre la valeur prédite et la valeur observée entrera dans la fonction d'erreur.
Ainsi Laplace a proposé une décomposition d'une variable observée en une somme de deux autres variables, mais différente de la décomposition «valeur vraie»+ erreur : il s'agit maintenant d'une décomposition valeur prédite d'après le modèle + fonction d'erreur ou résidu.
Quelle est la nature de cette fonction d'erreur ? En fait, la fonction d'erreur combine une multitude de facteurs d'origines très différentes. Ainsi, le résidu peut contenir une part liée à l'imprécision des instruments de mesure, une part liée à l'erreur humaine, etc.
Cette décomposition trouve aussi à s'appliquer aux mesures psychologiques mais, pour certains types de données psychologiques, ce passage ne va pas de soi. Ces problèmes sont expliqués plus en détail dans la grande leçon consacrée à la psychométrie.
Pour le moment, il suffit de retenir que la décomposition de la valeur observée en valeur vraie + erreur n'est pas la seule possible. Techniquement, la valeur vraie est souvent inconnue, voire même inconnaissable. La valeur prédite au contraire peut souvent être donnée a priori. Il est donc avantageux d'opérer une décomposition du type valeur observée = valeur prédite + fonction d'erreur.
3. Notion d'erreur statistique

Lorsque l'on essaie d'évaluer une valeur à partir d'un ensemble de mesures élémentaires, et qu'on fait la moyenne des observations obtenues, ce qu'on obtient n'est pas la valeur vraie de la mesure cherchée, mais seulement une estimation de cette valeur.
Tout d'abord, il peut y avoir des erreurs systématiques. Par exemple, si l'on mesure la largeur d'une planche avec une règle où les graduations sont trop rapprochées, on aura beau répéter les mesures un nombre infini de fois, le résultat moyen sera toujours plus grand que la largeur réelle.
Pour simplifier, imaginons que nous travaillons avec des instruments ne présentant pas de biais systématique. Il est alors possible de démontrer mathématiquement que si l'on répète un nombre infini de fois l'opération de mesure, et si l'on fait la moyenne de toutes les valeurs obtenues, alors la valeur moyenne tendra vers la valeur réelle.
Seulement dans la vie réelle, il est tout simplement impossible de répéter l'opération de mesure un nombre infini de fois. La moyenne d'un échantillon des valeurs tendra donc vers la moyenne réelle, mais elle ne l'atteindra jamais. L'écart entre la vraie valeur et la valeur estimée à partir de l'échantillon constitue l'erreur statistique.
Il faut remarquer ici que l'erreur statistique est donc la différence entre une valeur hypothétique, qui n'existe qu'idéalement, et la moyenne des valeurs observées.
5. Quantification de la variabilité
Objectif. Introduire le vocabulaire technique de base (variable, modalités, individu, population, ...) et l'idée de description formelle de caractéristiques observables. La quantification des relations sera traitée dans un autre article.
Prérequis. Leçon : variabilité due à l'erreur.
Résumé. Si la science consiste à construire des descriptions du réel, alors nous devons disposer d'un langage pour créer cette description. Le langage privilégié de la science est le langage logico-mathématique. Parmi tous les éléments de mathématiques, les nombres ont un statut privilégié. Dans cet article sont présentées les bases de l'attribution de nombres à des phénomènes réels, tels qu'on en rencontre en psychologie.
5.1. Pourquoi quantifier le réel ?

Nous l'avons vu dans les articles précédents, faire de la science consiste fondamentalement à produire un discours sur le réel. Ainsi définie, la science ne se distingue toutefois pas du langage ordinaire, au moins lorsque celui-ci s'applique à décrire la réalité. D'un autre côté, on sait bien que les livres de science comportent un mélange (savant, c'est le cas de le dire) de mots du langage ordinaire et de formules ésotériques dont la signification mystérieuse échappe au commun des mortels. Pourquoi les scientifiques s'embêtent-ils à apprendre et à utiliser un langage aussi compliqué ?
Certes, on pourrait imaginer qu'il s'agit uniquement des vestiges d'une époque révolue où les autorités ecclésiastiques protégeaient leurs prérogatives en se parant du mystère de la possession de la Connaissance. Mais cette explication est un peu courte. Une autre explication, plus naturelle, consiste à dire que la réalité est complexe et que, au fur et à mesure que les connaissances se développent, de nouveaux mots sont créés pour la décrire. Ainsi le langage d'une discipline s'enrichit-il progressivement au point de devenir inaccessible aux non-spécialistes. Certes. Cela ne fait aucun doute mais n'explique encore pas pourquoi les scientifiques s'évertuent à introduire des équations mathématiques et autres formalismes dans leurs discours... D'aucuns, surtout en psychologie, pourraient être tentés de prétendre que les mots devraient suffire, mais justement les mots ne suffisent pas. Les langages formels (mathématiques, langages informatiques...) sont plus complexes à apprendre car précisément ils ne nous sont pas naturels. Leur emploi oblige à une rigueur et une précision qui ne tolèrent pas cette ambiguité qui est paradoxalement un des avantages du langage naturel pour la communication sociale. Mais en retour, cette rigueur et cette précision réduisent le risque de construire des théories incohérentes, tandis qu'avec les constructions verbales en langage naturel, la puissance de la rhétorique autorise souvent des conclusions hasardeuses dont le caractère infondé passe inaperçu.

Plus encore, une fois acceptées et maîtrisées les contraintes d'emploi du langage formel, ce dernier devient un outil de raisonnement qui permet d'aboutir ainsi à des conclusions qu'il aurait été tout simplement impossible d'atteindre au moyen de la seule intuition. Ainsi, si l'on parvient à quantifier un phénomène, on peut alors appliquer aux valeurs obtenues les règles de combinaison en vigueur dans l'univers des nombres pour prédire le comportement des phénomènes étudiés. Certaines de ces règles reposent sur des théorèmes sophistiqués et permettent ainsi à tout un chacun d'utiliser sans avoir à les redécouvrir des modes de pensée développés par quelques uns des plus grands penseurs de l'histoire de l'humanité. On peut aussi mécaniser les traitements (i.e., les informatiser) et parvenir ainsi à élaborer des résultats ou des prédictions tout simplement inaccessibles par la pensée naturelle.
Nous allons maintenant explorer plus en détail les processus de quantification de la variabilité. Et, pour cela, nous allons devoir produire un certain nombre de définitions.
5.2. Individus, Populations, Échantillons
Notion d'individu

Étymologiquement, le terme individu renvoie aux racines latines in- et dividere , autrement dit « que l'on ne peut pas diviser ». On voit par là que l'individu est à la psychologie ce qu'est l'atome à la physique. Mona Lisa est un individu unique, distinct de tous les autres individus humains, que l'on peut reconnaître sans hésiter. Chaque individu humain est ainsi unique. Bien entendu, de même que les physiciens parviennent ensuite à décomposer l'atome en particules, on peut aussi décomposer l'individu (ou son système cognitif, puisque nous sommes en psychologie) en sous-parties qui peuvent elles-mêmes faire l'objet d'analyses.
Le terme technique qui capture l'idée d'individu dans le vocabulaire de la statistique est l'unité statistique. Ainsi, nous pouvons intégrer diverses informations au sujet d'une même unité statistique et ces informations auront en commun de décrire la même unité, le même individu.
L'usage en psychologie tend à abandonner l'habitude consistant à qualifier l'individu de « sujet », afin de faire référence à la personne en tant qu'elle n'est pas seulement un objet d'étude inerte, mais un individu auto-déterminé, autonome, capable d'une pensée propre et capable d'agir sur le monde. Cette tendance s'intensifie, comme en témoigne la récente introduction dans les normes de publications de l'APA (American Psychological Association) d'une règle selon laquelle on ne doit plus dans les articles scientifiques, qualifier les personnes qui participent aux expériences comme des "sujets", mais comme des "participants". Ce qui a le mérite de rendre claire la distinction entre les personnes humaines, incarnées, étudiées lors des expériences, et le sujet, idée abstraite, objet du discours produit par la science psychologique.
L'individu, sujet réel ou sujet idéalisé ?
En abordant la question de l'individu et de la population, il nous semble difficile d'ignorer un sujet qui fait encore parfois débat dans la communauté des psychologues : le rapport entre le statut du sujet et l'utilisation des statistiques.
Nous l'avons dit, la psychologie traite du sujet. Mais il faut distinguer la psychologie en tant que pratique clinique, celle où le praticien reçoit un patient dans son cabinet et traite cet individu dans ce qu'il a d'unique, et la psychologie en tant que science, où le chercheur vise à produire des connaissances valables pour tous les sujets humains, ou au moins pour certains groupes de sujets. De ce fait, lorsque l'on parle du sujet en psychologie scientifique, on parle d'un sujet idéalisé, un sujet reconstruit dans un univers de discours et non pas de monsieur X, en chair et en os, que l'on a devant nous. C'est ce qui fait dire à certains psychologues de sensibilité plus orientée vers la clinique que « les statistiques perdent le sujet ». Au point que certains rejettent l'usage des statistiques.
En réalité, les connaissances générales produites sur la population humaine, ou sur le sous-groupe d'humains dont monsieur X fait partie (« les hommes », par exemple) s'appliqueront généralement AUSSI à monsieur X. C'est tout l'intérêt appliqué de la recherche scientifique en psychologie ou en médecine : même si le clinicien est dans une logique qui ne requiert ni l'usage de statistiques ni de considérer un sujet idéalisé, il va bénéficier pour sa pratique des connaissances développées par les chercheurs, dont certaines trouveront à s'appliquer au cas particulier de son patient. Le clinicien utilise les connaissances générales développées par le chercheur. À ce titre, il n'a pas besoin des statistiques. Mais le chercheur, lui, a besoin des statistiques pour étayer les connaissances générales qu'il produit, et qui seront ensuite utilisées par le praticien. Le processus mental de pensée du chercheur est fondamentalement de produire un discours général capable d'expliquer, et même de prédire, des données observées dans le monde réel. C'est une approche dite inductive et les statistiques sont là pour l'aider à évaluer la qualité de son processus mental. Le processus mental du diagnosticien est différent : il s'appuie sur les connaissances générales développées par le chercheur, et sa tâche est de trouver à l'appliquer au cas particulier qu'il a devant lui. Il n'a donc aucune visée de généralisation et les statistiques ne peuvent rien pour lui, sinon à la rigueur pour le guider vers certaines hypothèses (les plus fréquentes) plutôt que vers d'autres.
Donc cela étant posé, il doit être clair que nous cherchons à produire une description du sujet humain, et que cette description est celle d'un individu appartenant à la population humaine globale, ou à l'un de ses sous-groupes.
Notions de population et d'échantillon

Par définition, une population est tout simplement un ensemble d'individus qui partagent une certaine caractéristique. Par exemple, la population française est l'ensemble des individus qui possèdent la nationalité française. En première intention, la psychologie étudie la population des organismes biologiques capables, à un degré ou à un autre, d'une certaine autonomie dans la production de leurs comportements. Mais bien sûr, on peut étudier des populations bien plus restreintes : la population des primates, la population des humains, celles des femmes, des adolescents... En général, dans la recherche, le chercheur va définir sa population à partir d'une caractéristique, ou d'un ensemble de caractéristiques, qui l'intéresse. La population étudiée sera l'ensemble des individus chez qui cette caractéristique a pour valeur la modalité souhaitée. Ainsi, la population d'un chercheur qui s'intéresse à la motivation chez les femmes sera l'ensemble des individus humains dont la modalité de la variable « sexe » est « féminin ».
Dans la plupart des cas, il ne sera pas possible d'étudier tous les individus de la population cible, pour des raisons évidentes de quantité de mesures à faire, de personnes à contacter... Si l'on veut produire des connaissances sur tous les humains, une population mondiale de plus de huit milliards de personnes disqualifie d'emblée cette possibilité. Le chercheur est donc obligé de recueillir des informations sur un sous-ensemble de la population cible, un échantillon, c'est-à-dire un sous-ensemble d'individus choisis pour leur représentativité. Le chercheur pourra alors produire des connaissances sur cette sous-population en espérant que les connaissances générées se généralisent bien au reste de la population cible.
Ces définitions étant posées, il nous faut maintenant introduire d'autres concepts qui vont nous permettre de décrire plus finement les individus, et aussi de dégager des points communs entre individus et ainsi formaliser les critères d'appartenance à une population. Ce sont les notions de variables, valeurs et modalités qui vont nous y aider.
5.3. Variables, valeurs et modalités
3.1. Définitions
Considérons la définition suivante :
Une variable est une propriété d'un objet ou événement qui peut prendre différentes valeurs. Ainsi la couleur des cheveux est une variable parce qu'il s'agit de la propriété d'un objet (les cheveux) et qu'elle peut prendre différentes valeurs (cheveux bruns, blonds, roux, gris, etc.)
David C. Howell (2008, p. 4)

On voit qu'ainsi définie, la notion de variable est une notion extrêmement générale, qui nous permettra de décrire des objets sous l'angle des valeurs que peuvent prendre les propriétés de ces objets. Lorsque ces valeurs correspondent à des éléments discrets (c'est-à-dire suffisamment séparés pour qu'on puisse les compter), on appelle chacune de ces valeurs modalités. Dans l'exemple précédent de Howell, bruns, blonds, roux, etc. sont autant de modalités de la variable couleur des cheveux. Lorsque la variable peut prendre une infinité de valeurs sur un intervalle (mathématiquement parlant, lorsque l'intervalle est « continu »), par exemple lorsque l'on mesure la taille ou le poids d'un individu, on ne parle généralement plus de modalités mais de valeurs.
La notion de variable correspond à des propriétés communes à toute une classe d'objets. Par exemple si on s'intéresse à la classe des humains, on pourra assigner une modalité à la variable « couleur des cheveux » pour tout individu. Cette variable pourra changer de modalité en passant d'un individu à l'autre, même si elle est constante pour un même individu. A l'inverse, certaines variables peuvent changer de modalité chez un même individu observé à des moments différents. Par exemple, la variable « couleur des cheveux » peut changer si un individu se fait teindre les cheveux.
Attention : il ne faut pas confondre la notion de variable telle que nous venons de la définir, avec la notion de variable aléatoire, beaucoup plus spécifique et sur laquelle nous reviendrons.
3.2. Les types de variables
Suivant le type de modalités ou d'échelles de mesure utilisée pour coder une variable, celle-ci possédera différentes propriétés. On distingue trois types de variables, correspondant à trois types d'échelles de mesures.
- Les variables nominales. Ce sont des variables qui servent à coder des caractéristiques bien séparées (discrètes) de sorte que les différents individus peuvent être regroupés en catégories mutuellement exclusives selon la modalité que prend pour eux
 cette variable. Par exemple, si la caractéristique est « couleur des cheveux », et que l'on code cette couleur avec les modalités vues plus haut dans la définition de Howell (cheveux bruns, blonds, roux, ...) on voit facilement qu'il est possible de constituer des classes d'individus (les bruns, les roux, les blonds, ...) et qu'un individu donné ne sera affecté qu'à une seule classe à l'exclusion des autres. Un cas particulier de variable nominale est particulièrement intéressant : les variables dichotomiques. Il s'agit de variables ne possédant que deux modalités. Par exemple, la variable Sexe chez les humains ne peut prendre que les modalités Masculin ou Féminin. On peut donc très facilement les recoder en 0 et 1, ce qui autorise certains traitements de type numérique bien que la variable soit fondamentalement nominale.
cette variable. Par exemple, si la caractéristique est « couleur des cheveux », et que l'on code cette couleur avec les modalités vues plus haut dans la définition de Howell (cheveux bruns, blonds, roux, ...) on voit facilement qu'il est possible de constituer des classes d'individus (les bruns, les roux, les blonds, ...) et qu'un individu donné ne sera affecté qu'à une seule classe à l'exclusion des autres. Un cas particulier de variable nominale est particulièrement intéressant : les variables dichotomiques. Il s'agit de variables ne possédant que deux modalités. Par exemple, la variable Sexe chez les humains ne peut prendre que les modalités Masculin ou Féminin. On peut donc très facilement les recoder en 0 et 1, ce qui autorise certains traitements de type numérique bien que la variable soit fondamentalement nominale.
Enfin, il faut noter qu'on emploie parfois l'expression échelle nominale pour désigner l'ensemble des valeurs possibles d'une variable nominale, mais il faut être conscient qu'il s'agit là d'un abus de langage, car les différentes modalités d'une variable nominale sont seulement juxtaposées et ne constituent en aucun cas une entité orientée, ordonnée comme peut l'être une échelle.
Les échelles nominales posent un problème immédiat : elles ne possèdent presque aucune des propriétés des nombres. Or, ce que nous cherchons dans cet article, c'est d'exposer une démarche de quantification de la réalité. Ce problème se résout par le fait qu'on introduit la notion de fréquence. Autrement dit, puisque nous disposons de catégories discrètes et d'individus qui se répartissent dans les différentes catégories de la variable, il est possible, tout simplement, de compter le nombre d'individus dans chaque catégorie. En divisant le nombre d'éléments d'une catégorie par le nombre total d'individus, nous obtenons la fréquence de la catégorie. Nous pourrons dès lors appliquer les propriétés mathématiques des fréquences pour procéder aux analyses quantitatives sur les variables d'intérêt pour la recherche. - Les variables ordinales. Ce sont des variables dont les modalités peuvent être des intervalles ou des nombres, mais dont seule la propriété d'ordre (d'où le terme « ordinal ») est prise en compte. Considérons par exemple les classes d'âge suivantes : moins de 20 ans, de 20 à 39 ans, de 40 à 59 ans, de 60 à 80 ans, plus de 80 ans. Ces catégories pourraient tout à fait tomber dans le cadre de la définition des variables nominales vues précédemment puisqu’un individu donné appartient sans ambiguïté à une et une seule de ces catégories. Toutefois, contrairement au cas des variables nominales, ces catégories sont ordonnées, au sens où il existe une relation comparative entre elles. Tout individu appartenant à la classe des 20-39 ans est plus vieux que tout individu de la classe des moins de 20 ans. Autre exemple : On peut mettre des notes ordinales aux devoirs d'élèves, A+, A-, B+, B-, etc. On dit qu’il existe une
 relation d’ordre entre les modalités de la variable. Les variables ordinales peuvent avoir des nombres ordinaux comme modalités. Par exemple, si l’on met 1 au premier de la classe (celui qui a la meilleure moyenne), 2 au deuxième, 3 au troisième, et... On voit que les nombres ainsi obtenus traduisent un classement, un ordre. Par contre, on voit bien aussi que ces nombres ne respectent pas une propriété cruciale, dite « égalité des intervalles ». Derrière cette expression compliquée se cache l'idée que les intervalles (on peut toujours imaginer l'intervalle entre 2 et 3) n’ont pas la même signification. Ainsi, rien ne permet d’affirmer que la différence qui existe entre le 1er et le deuxième de la classe est la même que celle qui existe entre le deuxième et le troisième. Il y a peut-être un gouffre entre le deuxième et le troisième alors que la place de 1er s’est jouée à un petit rien sans importance. Une autre différence tient à ce que les variables ordinales peuvent être continues et non pas discrètes. Par exemple, si l'on mesure la compétence d’après le temps passé à traiter un problème complexe. La variable peut être considérée comme continue
[1]
, mais cela n’aurait pas de sens de dire qu’un individu est deux fois plus compétent qu’un autre s’il a mis deux fois moins de temps. On ne peut donc retenir que la propriété d’ordre : de deux participants, le plus rapide sera juste considéré comme plus compétent.
relation d’ordre entre les modalités de la variable. Les variables ordinales peuvent avoir des nombres ordinaux comme modalités. Par exemple, si l’on met 1 au premier de la classe (celui qui a la meilleure moyenne), 2 au deuxième, 3 au troisième, et... On voit que les nombres ainsi obtenus traduisent un classement, un ordre. Par contre, on voit bien aussi que ces nombres ne respectent pas une propriété cruciale, dite « égalité des intervalles ». Derrière cette expression compliquée se cache l'idée que les intervalles (on peut toujours imaginer l'intervalle entre 2 et 3) n’ont pas la même signification. Ainsi, rien ne permet d’affirmer que la différence qui existe entre le 1er et le deuxième de la classe est la même que celle qui existe entre le deuxième et le troisième. Il y a peut-être un gouffre entre le deuxième et le troisième alors que la place de 1er s’est jouée à un petit rien sans importance. Une autre différence tient à ce que les variables ordinales peuvent être continues et non pas discrètes. Par exemple, si l'on mesure la compétence d’après le temps passé à traiter un problème complexe. La variable peut être considérée comme continue
[1]
, mais cela n’aurait pas de sens de dire qu’un individu est deux fois plus compétent qu’un autre s’il a mis deux fois moins de temps. On ne peut donc retenir que la propriété d’ordre : de deux participants, le plus rapide sera juste considéré comme plus compétent.
Notons que, contrairement aux modalités des soi-disant « échelles nominales », les modalités d'une variable ordinale sont bel et bien orientées et l'on est donc tout à fait fondés à parler d'échelle ordinale. -
Les variables numériques. Supposons maintenant que l'on mesure la taille d'un individu. Cette fois, l'échelle de
 mesure est bien un nombre, mais ce nombre possède la propriété d'égalité des intervalles. Cela signifie tout simplement que la différence de taille entre 0,50m et 1m est la même qu'entre 1m et 1,5m. Cette propriété n'était pas respectée avec les échelles ordinales. Ue variable qui satisfait cette propriété est aussi appelée variable d'intervalles (on parlera de variable mesurée sur une échelle d'intervalles). Il existe un dernier raffinement, lorsque les valeurs ont toutes les propriétés des variables numériques d'intervalle, plus une nouvelle propriété, à savoir qu'il existe en plus un vrai zéro de la mesure. Un vrai zéro (ou « zéro absolu » comme disent les physiciens) est la valeur où la grandeur mesurée est effectivement nulle. On parle alors de variables de rapport et d'échelles de rapport. En effet, le zéro constitue alors un point de référence commun à tous les rapports qui, du coup, prennent sens les uns par rapport aux autres. On peut dire que quelqu'un de deux mètres est deux fois plus grand que quelqu'un de 1m, que quelqu'un de 1,80 m est deux fois plus grand que quelqu'un de 90 cm, et dans les deux cas, « deux fois plus grand » signifie la même chose. Mais tant que les physiciens n'avaient pas trouvé le zéro absolu des températures, ils ne pouvaient comparer les rapports de températures mesurées par Celsius, par exemple, avec les rapports de températures mesurés en Fahrenheit. Pou prendre un exemple en psychologie, avec une échelle d'intelligence, le zéro serait l'absence totale d'intelligence. Mais quelle signification une telle idée peut-elle avoir. C'est, à ce jour, indéfini. Dans ces conditions, il est impossible de dire que l'intelligence est notée sur une échelle de rapport. En l'absence d'un zéro absolu, les rapports entre les nombres ne sont pas comparables. Autrement dit, affirmer que quelqu'un est deux fois plus intelligent que quelqu'un d'autre n'a aucun sens. Tout au plus peut-on dire que l'un est plus intelligent que l'autre, ou, sous une forme plus générale, dire que dans une population de 1000 personnes, telle personne se classerait probablement dans les 10 plus intelligents.
mesure est bien un nombre, mais ce nombre possède la propriété d'égalité des intervalles. Cela signifie tout simplement que la différence de taille entre 0,50m et 1m est la même qu'entre 1m et 1,5m. Cette propriété n'était pas respectée avec les échelles ordinales. Ue variable qui satisfait cette propriété est aussi appelée variable d'intervalles (on parlera de variable mesurée sur une échelle d'intervalles). Il existe un dernier raffinement, lorsque les valeurs ont toutes les propriétés des variables numériques d'intervalle, plus une nouvelle propriété, à savoir qu'il existe en plus un vrai zéro de la mesure. Un vrai zéro (ou « zéro absolu » comme disent les physiciens) est la valeur où la grandeur mesurée est effectivement nulle. On parle alors de variables de rapport et d'échelles de rapport. En effet, le zéro constitue alors un point de référence commun à tous les rapports qui, du coup, prennent sens les uns par rapport aux autres. On peut dire que quelqu'un de deux mètres est deux fois plus grand que quelqu'un de 1m, que quelqu'un de 1,80 m est deux fois plus grand que quelqu'un de 90 cm, et dans les deux cas, « deux fois plus grand » signifie la même chose. Mais tant que les physiciens n'avaient pas trouvé le zéro absolu des températures, ils ne pouvaient comparer les rapports de températures mesurées par Celsius, par exemple, avec les rapports de températures mesurés en Fahrenheit. Pou prendre un exemple en psychologie, avec une échelle d'intelligence, le zéro serait l'absence totale d'intelligence. Mais quelle signification une telle idée peut-elle avoir. C'est, à ce jour, indéfini. Dans ces conditions, il est impossible de dire que l'intelligence est notée sur une échelle de rapport. En l'absence d'un zéro absolu, les rapports entre les nombres ne sont pas comparables. Autrement dit, affirmer que quelqu'un est deux fois plus intelligent que quelqu'un d'autre n'a aucun sens. Tout au plus peut-on dire que l'un est plus intelligent que l'autre, ou, sous une forme plus générale, dire que dans une population de 1000 personnes, telle personne se classerait probablement dans les 10 plus intelligents.
[1] Même si dans la pratique on ne dispose jamais d’une précision infinie, mais c’est un autre problème.
5.4. La quantification en psychologie, mesure ou codage ?
Jusqu'ici nous avons introduit les outils conceptuels qui vont nous permettre de décrire la réalité sous une forme mathématique, grâce en particulier aux concepts d'individu, de variable, et de population. Grâce à ces concepts, nous sommes en mesure de penser la réalité psychologique. Il reste que pour appliquer ces outils conceptuels à des situations concrètes, il va nécessairement falloir passer par une étape où la réalité observée sera traduite, codée, en termes des variables que nous nous serons données et des modalités que nous avons définies pour ces variables. La question du codage de la réalité perçue en langage formel, et des conditions de bonne réalisation de ce codage, est au cœur de la psychométrie, mais aussi au cœur de la statistique qui ne pourrait s'appliquer sans cela.
Peut-on parler de mesure en psychologie ?
Spontanément, on aurait envie de dire que mettre des nombres sur la réalité empirique, c'est précisément ce que l'on fait quand on réalise un mesurage, autrement dit qu'on mesure un objet de la réalité. Examinons de plus près cependant ce que cela signifie. Considérons la définition suivante du terme « mesure » :
Action de déterminer la valeur de (une grandeur) par comparaison avec une grandeur constante de même espèce, prise comme terme de référence.

On voit là que la mesure est prise comme rapport par rapport à une valeur étalon. Par exemple, la valeur étalon étant le mètre, dire d'un individu qu'il mesure 1,73 m signifie que sa taille est dans un rapport de 1,73 avec le mètre étalon. Comme le remarque Stéphane Vautier (in « Cours de Psychométrie, Notions élémentaires de la théorie classique des tests ») :
Si l'on peut définir une unité de mesure de la grandeur comme par exemple le mètre pour les distances ou le gramme pour les masses, les problèmes de mesure reviennent essentiellement à améliorer la précision et la fiabilité des instruments.
Mais l'on voit immédiatement que cette définition pose un problème au psychologue car, comme nous l'avons vu dans la page précédente, les variables auxquelles doit faire face ce dernier sont loin de toujours posséder les propriétés d'une variable de rapport. D'où le problème résumé dans la citation suivante :
Au sens large, "mesurer" c'est faire correspondre des nombres aux choses selon certaines règles, c'est faire correspondre certaines propriétés des choses avec certaines propriétés des nombres (...) la difficulté réside alors dans l'isomorphie ou l'adéquation plus ou moins forte entre les propriétés des nombres - établies dans le monde mathématique - et les propriétés de la variable étudiée - établies dans le monde psychologique, sociologique, médical etc (...)
B. Beaufils, in Études de statistiques descriptives. Cours du CNED.
Dans certains cas, cette adéquation semble assez directe. Par exemple, quand le psychologue cognitiviste mesure des temps de réponse, ces temps possèdent toutes les propriétés bien connues des mesures de temps. Mais dans d'autres cas, cette correspondance est loin d'être évidente et doit reposer sur des méthodes indirectes.
On ne saurait restreindre la légitimité de la mesure aux seuls cas où l'on peut la fonder sur une axiomatique permettant une vérification directe. Il importe cependant, dans les autres cas, d'avoir une claire conscience des hypothèses sur lesquelles est fondée la technique de mesure et de garder le souci d'en tester la validité de manière indirecte.
Jean-François Richard. in Sciences Humaines - Mesures, Encyclopedia Universalis.
La notion de codage

Dans ces conditions, comment appeler le processus d'attribution d'une valeur ou d'une modalité à une variable à partir de l'observation de la caractéristique correspondante d'un individu ? Une solution serait d'utiliser le terme « observation ». Malheureusement, ce dernier est encore plus problématique pour plusieurs raisons. La plus importante est que l'usage dans les sciences en général (cela dépasse largement la discipline psychologique) est d'opposer l'observation à l'expérimentation. L'observation est conçue comme une méthode de recueil de données sur une réalité accomplie de façon à ne pas perturber cette dernière, tandis que l'expérimentation passe au contraire par la manipulation directe des conditions du recueil de données. Or, nous cherchons une terminologie qui doit pouvoir s'appliquer indifféremment dans ces deux cas.
Dans ce site, nous adopterons donc la démarche suivante : nous qualifierons de codage l'opération qui consiste à attribuer un nombre ou une catégorie à des objets empiriques. Nous parlerons de codage numérique lorsque le résultat du codage utilisera une variable numérique, codage ordinal, lorsqu'il s'agira d'une échelle seulement ordinale.
6. Variabilité et distributions
Objectif. Poursuivre l'introduction du vocabulaire technique de base, en précisant bien les statuts des différents concepts servant à décrire les distributions.
Prérequis. Leçon : quantification de la variabilité.
Résumé. On étudie généralement une population au travers d'un échantillon représentatif. En compilant les observations réalisées sur l'échantillon, on obtient une estimation servant à approcher la valeur d'un paramètre, c'est-à-dire la valeur idéale qu'on pourrait obtenir si l'on faisait des mesures parfaites sur absolument tous les individus de la population cible.
6.1. Notion de distribution
Pourquoi caractériser une population ? Un exemple concret.

Imaginons que des fabricants de vêtements souhaitent mesurer la taille moyenne des français, afin de savoir de quelles tailles ils doivent fabriquer leurs vêtements. Une procédure évidente, à condition de disposer de moyens quasi illimités, consisterait à mesurer chacun des individus qui composent la population française, soit plus de soixante millions de mesures. Admettons pour l'instant que le coût de ces mesures ne soit pas un problème et tournons-nous plutôt vers l'utilisation que les industriels pourraient faire de l'information recueillie.
La première remarque, c'est qu'au sein d'une population d'apparence homogène peuvent se cacher des populations différentes. Ainsi, du point de vue de la taille, la population française n'est pas homogène. Il suffit de considérer la question du sexe pour qu'il soit évident que les proportions des hommes et des femmes adultes ne sont pas identiques. Ainsi, du point de vue de la taille, la population française est composée du regroupement de deux populations différentes : les hommes et les femmes. En fait, on sait aussi que, toujours du point de vue de la taille, les proportions des enfants (la taille de la tête par rapport au reste du corps, par exemple) ne sont pas les mêmes que les proportions des adultes. Pour la simplicité de l'exposé, imaginons que nos industriels ne souhaitent habiller que la population des hommes adultes.
S'ils veulent rentabiliser leurs usines, ces industriels devraient pouvoir fabriquer une quantité de vêtements de grandes tailles proportionelle à la part de grandes personnes en France. Même chose pour les petites tailles et les moyennes tailles. On voit bien qu'il ne servirait pas à grand-chose de seulement produire des vêtements d'une taille adaptée au français moyen !
La question qui se pose ensuite à nos fabricants est de déterminer combien de sortes de tailles de vêtements différents, il va falloir fabriquer. Si un vêtement est taillé pour des individus petits (Taille S), tous les individus entrant dans cette classe doivent pouvoir porter le vêtement. Mais il est clair qu'un individu de grande taille (taille XXL) ne pourrait pas porter ce même vêtement, car il ne pourrait pas rentrer dedans sans le craquer, ou bien il serait mal dedans et aurait l'air ridicule. Par ailleurs, les procédés industriels sont tels qu'on peut réduire les coûts si on fabrique un nombre petit de modèles différents. On ne peut donc pas non plus fabriquer des vêtements pour chaque taille exacte. Les fabricants vont donc définir le plus petit nombre possible de classes d'équivalence pour décrire la population. Par classes d'équivalence, il faut entendre ici des intervalles de tailles de sujets tels que tous les individus mesurant entre la limite basse et la limite haute pourront physiquement porter les mêmes vêtements.
Une fois ces classes définies, nos fabricants doivent répondre à deux nouvelles questions :
- Combien de vêtements de chaque classe peuvent-ils vendre ? Et donc combien il y a d'individus dans chaque classe ?
- Quelle taille devront avoir les vêtements de chaque classe ?
La première question est celle de l'effectif. Autrement dit, combien d'individus tombent dans cette classe. Connaître l'effectif de l'échantillon est aisé : il suffit de compter. Dans certains cas, on préférera utiliser la notion de fréquence, sur laquelle nous reviendrons.
La deuxième question est plus délicate, car même en connaissant exactement la taille de chaque individu de la population, il existe plusieurs réponses. On peut par exemple choisir la taille la plus grande dans cet intervalle, en se disant que comme cela on est sûr que tout le monde rentrera dedans... On peut aussi choisir la taille moyenne des individus de cette classe, l'idée étant de minimiser l'écart de taille qu'aura à subir chaque consommateur (entre sa taille réelle et la taille du vêtement), et donc augmenter les chances que des acheteurs potentiels trouvent que le vêtement leur va.
Définition de distribution

Toutes les questions précédentes ont un point commun : y répondre suppose d'avoir une idée de la répartition des individus de la population sur la caractéristique considérée. C'est précisément la notion de distribution .
Définition : Nous appellerons distribution d'une population sur une caractéristique la répartition des individus de la population sur les différentes modalités ou valeurs de la caractéristique.
Nous pouvons d'ores et déjà noter que les distributions ont été étudiées sous l'angle des fonctions mathématiques qui permettent d'en donner un modèle. L'exemple le plus connu est la fameuse courbe en cloche, qui traduit la répartition que prennent les mesures autour d'une valeur moyenne lorsque seul le hasard (l'imprécision de la mesure) explique la dispersion des notes autour de la moyenne. Cette courbe a différentes propriétés mathématiques sur lesquelles nous reviendrons. Par exemple, elle est symétrique autour de la moyenne, on rencontre le plus d'observations près de la moyenne et plus on s'éloigne de la moyenne, moins on trouve d'observations, etc. Le belge Adolphe Quetelet en particulier s'est illustré pour avoir mis en évidence cette distribution sur des données humaines.
Ainsi, on a d'un côté les distributions empiriques observées (la répartition des tailles chez les individus d'un échantillon représentatif) ou non (la répartition des tailles dans l'ensemble de tous les français) et les distributions mathématiques (par exemple la distribution induite par l'imprécision de la mesure).
6.2. Paramètres et statistiques
Bien entendu, il est peu probable qu'on se lance jamais dans l'enquête prise précédemment en exemple, car celle-ci aurait un coût exorbitant. Ce coût serait d'autant plus difficile à justifier que, même en admettant qu'on ait besoin de connaître les tailles des français avec précision, on peut imaginer que si on prend un échantillon bien choisi de français, c'est-à-dire un échantillon choisi pour être représentatif de l'ensemble de la population française, alors la moyenne observée sur l'échantillon serait très proche de la moyenne réelle. De sorte que le gain de précision qu'on pourrait espérer en mesurant vraiment toute la population cible ne pourrait jamais compenser le coût exorbitant d'une telle étude. C'est effectivement la stratégie que chercheurs comme industriels utilisent dans la quasi-totalité des cas : recueillir des données sur un échantillon bien choisi d'individus et en inférer les propriétés de la population cible. C'est précisément l'objet de la statistique que de fournir des informations sur les populations à partir des données d'échantillons extraits de ces populations .
Définitions
Considérons maintenant la définition suivante, discutable à plusieurs égards, mais qui va nous servir de point de départ :
« Une mesure, comme le score moyen d’autosatisfaction, qui se réfère à l’ensemble d’une population est appelée paramètre . Cette même mesure est appelée statistique lorsqu’elle est calculée à partir d’un échantillon de données que nous avons rassemblées. Les paramètres sont des entités réelles d’intérêt tandis que les statistiques correspondantes sont en fait des suppositions »
David Howell (2008, p. 5).

Laissons pour le moment de côté la question de savoir si un score d'auto-satisfaction est vraiment une mesure pour nous concentrer sur la distinction entre les concepts de paramètre et de statistique, extrêmement importante à comprendre. En effet, à première vue, on pourrait croire que les seules informations « réelles » sont celles recueillies sur l'échantillon, tandis que celles portant sur la population ne sont qu'inférées à partir des données de l'échantillon. Nous pourrions donc être tentés de considérer les statistiques comme réelles et le paramètre comme hypothétique. Pour lever cette difficulté, il faut adopter un point de vue différent, développé au début du XX siècle par
Karl Pearson
(image ci-contre). Pour Pearson, le paramètre, terme dont l'étymologie renvoie au grec pour « à côté de la mesure », est réel et digne d'intérêt parce que, du point de vue de la recherche, c'est sur lui qu'on veut apprendre quelque chose. Du point de vue scientifique, il n'est a priori intéressant d'apprendre des choses sur un échantillon particulier que dans la mesure où ces choses nous renseignent sur l'ensemble de la population qu'on veut étudier. Il ne serait pas intéressant de savoir que telle expérience a donné tel résultat si en même temps elle ne nous apprenait pas quelque connaissance générale sur le monde. C'est donc bel et bien le paramètre, qui n'est pas la mesure, mais qui est estimé grâce à elle, qui est « d'intérêt », pour reprendre l'expression de Howell.
siècle par
Karl Pearson
(image ci-contre). Pour Pearson, le paramètre, terme dont l'étymologie renvoie au grec pour « à côté de la mesure », est réel et digne d'intérêt parce que, du point de vue de la recherche, c'est sur lui qu'on veut apprendre quelque chose. Du point de vue scientifique, il n'est a priori intéressant d'apprendre des choses sur un échantillon particulier que dans la mesure où ces choses nous renseignent sur l'ensemble de la population qu'on veut étudier. Il ne serait pas intéressant de savoir que telle expérience a donné tel résultat si en même temps elle ne nous apprenait pas quelque connaissance générale sur le monde. C'est donc bel et bien le paramètre, qui n'est pas la mesure, mais qui est estimé grâce à elle, qui est « d'intérêt », pour reprendre l'expression de Howell.
Ce qui paraît curieux dans la définition vue plus haut, c'est l'affirmation que la statistique est une supposition. En effet, on pourrait penser que c'est finalement la seule donnée un peu solide dont nous disposons. Au moins elle renseigne sur quelque chose qui a été effectivement observé. En fait, Pearson a proposé de renverser ce point de vue et de considérer que ce qui est réel ce sont les fonctions mathématiques qui servent à décrire comment se répartissent les observations. Si vous vous rappelez le schéma vu dans l'article d'introduction, vous n'aurez aucun mal à voir qu'il s'agit là d'une position qui distingue des croyances que l'on pourrait qualifier de « vraies » et des croyances plus ou moins trompeuses. Dans cette optique, les observations réalisées ne sont que des expériences fortement dépendantes de petits événements aléatoires et ne sont donc pas réelles, mais seulement des valeurs plus ou moins trompeuses. Soit. Mais...
Le paramètre est-il réel ?
C'est généralement ce que l'on suppose. Ainsi, on peut s'interroger sur la taille moyenne de la population française. Cette taille moyenne est un paramètre et elle existe indubitablement dans l'univers mathématique. La question devient alors celle de la réalité de l'univers mathématique. Il s'agit là d'une position philosophique discutable et discutée, même chez les mathématiciens. Sans nécessairement aller jusqu'à une position extrême comme le rationalisme de Platon, certains mathématiciens dits spiritualistes considèrent que l'univers mathématique possède une réalité intrinsèque que le chercheur ne fait que découvrir. D'autres ont une position plus constructiviste et considèrent que les mathématiques ne sont qu'une construction de l'esprit humain.
Quoi qu'il en soit au plan philosophique, ne nous y trompons pas : la valeur exacte d'un paramètre décrivant une population nous est généralement inconnue, quand elle n'est pas franchement inconnaissable. On ne peut généralement en obtenir qu'une approximation, et c'est précisément ce à quoi sert la statistique calculée à partir des données recueillies sur l'échantillon : nous fournir une estimation de la valeur du paramètre.
Dans le cadre de la présente leçon d'introduction, nous restons au niveau des concepts très fondamentaux et nous ne rentrerons pas plus avant dans la description des distributions. Ces points seront traités plus en détail dans la grande leçon intitulée Statistique descriptive.
7. Relations entre Statistique et Psychométrie
Objectifs . Apporter des éléments de réponse à la question : quelles différences et points communs y a-t-il entre statistique et psychométrie ?
Prérequis. Mesure, mesurage et codage numérique ; Scores psychométriques.
- Une différence : la statistique produit des méthodes d'analyse des données tandis que la psychométrie produit des méthodes de recueil des données.
- Trois points communs : statistique et psychométrie (1) utilisent des échelles de mesure, (2) utilisent le langage des mathématiques, (3) s'appuient sur la théorie des probabilités.
7.1. La statistique et la psychométrie utilisent des échelles de mesure

Dans un article de 1946, intitulé "On the theory of scales of measurement" (De la théorie des échelles de mesure), Stevens propose de surmonter le scepticisme d'une partie de la communauté scientifique quant à la possibilité de mesurer les sensations, en distinguant différents types d'échelles de mesure. Sa démarche s'oppose à la tradition selon laquelle ne sont mesurables que les grandeurs pour lesquelles on sait définir une unité de mesure ayant une signification expérimentale (on peut aussi dire empirique ou opérationnelle).
Stevens redéfinit la mesure comme l'attribution de nombres à des objets ou à des événements selon certaines règles. L'article Échelles de mesure présente en détail les différentes échelles de mesure. Dans le cadre de ce paragraphe, il sera suffisant de savoir reconnaître les différents types d'échelles : Échelle nominale, Échelle ordinale, Échelle d'intervalle, Échelle de ratio.
1.1. Échelle nominale
Caractériser les individus selon leur sexe nécessite l'utilisation d'une échelle nominale. Les catégories de cette échelle sont la catégorie Fille d'une part, la catégorie Garçon d'autre part. On remarquera que les catégories de l'échelle sont les modalités de la variable Sexe.
On peut coder 1 et 2 les catégories, mais la proposition 1 < 2 n'a pas de sens, il n'y a pas de sens non plus à appliquer l'addition ou la soustraction à ces nombres. Les seules opérations logiques qui ont un sens sont l'égalité et la différence (avoir le même sexe ou avoir des sexes opposés).
1.2. Échelle ordinale
Caractériser les individus selon leur niveau de compétence dans un domaine particulier nécessite une échelle ordinale. Par exemple, un jury peut attribuer un score variant de 0 à 100 à 10 candidats, de manière que les candidats puissent être classés.
On peut coder 1, 2, ..., 100 les niveaux de compétence que le jury peut attribuer à tout candidat, mais il n'y a pas de sens à appliquer l'addition ou la soustraction à ces scores : en effet, l'opération + ou l'opération - n'ont pas de signification définie dans le domaine conceptuel des niveaux de compétences. Il est possible que les décisions qui conduisent le jury à ordonner les 10 candidats ne soient pas explicites ; dans ce cas, l'échelle ordinale n'a pas d'interprétation expérimentale claire, et on peut mettre en question sa capacité à décrire la réalité des compétences des candidats.
1.3. Échelle d'intervalle
Les scores attribués à des individus pour les différencier de manière ordinale sont très souvent traités comme s'ils étaient définis sur une échelle d'intervalle. Comme son nom l'indique, une échelle d'intervalle est fondée sur la notion d'intervalle. Sur une échelle d'intervalle, un intervalle d'une valeur donnée représente la même variation, quelle que soit la valeur prise par la borne inférieure (ou supérieure) de cet intervalle dans l'ensemble des valeurs admissibles. Ainsi, par exemple, on considère généralement que la différence entre un score de QI de 100 et un score de QI de 85, soit un intervalle de 15 points de QI, représente la même variation d'intelligence que la différence entre un score de QI de 120 et un score de QI de 105, soit un intervalle de même valeur (15 points de QI). Un tel énoncé est une convention de langage tant que l'on ne sait pas définir expérimentalement à quoi correspond un intervalle quelconque au niveau de l'intelligence.
7.2. La statistique et la psychométrie utilisent le langage des mathématiques

Mauvaise nouvelle : la moyenne et la variance sont des concepts mathématiques. La covariance est aussi un concept mathématique. Ces trois concepts sont fondamentaux en statistique et en psychométrie.
Bonne nouvelle : la maîtrise du langage mathématique nécessaire pour définir ces concepts ne nécessite pas des études poussées ni un QI supérieur à la moyenne !
Le langage mathématique dont nous aurons besoin est basé sur les opérations algébriques usuelles
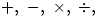
dans l'ensemble des nombres réels, noté 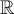 .
.
1.4. Échelle de ratio
Les échelles de ratio permettent de mesurer des grandeurs au sens classique du terme. Par exemple, compter le nombre de bonbons que l'on trouve dans un paquet de 125 grammes produit une mesure sur une échelle de ratio. Les nombres utilisés représentent de manière unique les quantités de bonbons. La mesure est définie comme la proportion définie par le rapport de deux quantités, la quantité de bonbons rapportée à la quantité 1. Dans le cas des grandeurs continues, la quantité 1 est définie conventionnellement par référence à un étalon.
7.3. La statistique et la psychométrie s'appuient sur la théorie des probabilités

On verra que pour être utilisé comme une mesure, un score psychométrique est défini comme un événement aléatoire. Un événement aléatoire est défini de manière précise dans le cadre d'un espace de probabilités. Un espace de probabilités suppose en particulier un ensemble d'événements possibles, nécessaire pour pouvoir y définir une probabilité. Ces concepts d'événement aléatoire, d'ensemble des événements, de probabilité définie sur un ensemble d'événements, appartiennent à la théorie des probabilités.
Plus tard dans le cursus de psychologie, on verra que l'estimation d'un intervalle de confiance associé à un paramètre statistique, par exemple la moyenne, repose sur une approche probabiliste : la moyenne associée à un échantillon d'unités d'observation est conçue comme un événement aléatoire.
Ainsi, la psychométrie, qui s'occupe de la conceptualisation des scores obtenus à l'aide de tests ou questionnaires psychométriques, et la statistique, qui s'occupe de l'estimation de paramètres statistiques caractérisant une ou des populations d'individus, reposent sur un même socle théorique : la théorie des probabilités.
7.4. On fait des analyses statistiques des scores psychométriques

Les phénomènes psychologiques peuvent être appréhendés de manière statistique. Par exemple, dans le domaine de la psychologie des intérêts, qui trouve ses applications dans le champ de l'orientation scolaire et professionnelle, on peut avoir l'impression que les femmes s'intéressent plus au domaine de la psychologie que les hommes. Mais sur quoi fonder une telle impression ? Avant de se lancer dans des explications savantes, il convient de mieux cerner le phénomène, c'est-à-dire de le caractériser de manière objective.
Il s'agit donc d'évaluer la relation de dépendance statistique entre le sexe et l'intérêt pour les disciplines de la psychologie. Pour cela, on peut tout d'abord circonscrire une population d'étude, par exemple en s'intéressant aux étudiants inscrits en L1 à l'UFR de Psychologie de l'Université de Toulouse, puis comparer le pourcentage de femmes au pourcentage d'hommes (environ 90% vs. 10%). Cette approche du problème repose sur l'utilisation de l'inscription en première année de psychologie comme d'un indicateur de l'intérêt des étudiants pour la psychologie.
On peut aussi objectiver le phénomène de dépendance statistique entre sexe et intérêt pour la psychologie en s'appuyant sur des mesures psychométriques de l'intérêt pour la psychologie dans la population générale et non pas seulement dans la population des étudiants de psychologie. Muni d'une technique de quantification appropriée, on pourra alors circonscrire la population d'étude comme la population des adultes français, faire une enquête auprès d'un échantillon représentatif, et comparer la moyenne des scores d'intérêt des femmes à la moyenne des scores d'intérêt des hommes. Si l'impression initiale est fondée et si l'on a correctement mesuré l'intérêt pour la psychologie, le score moyen des femmes devrait être nettement supérieur au score moyen des hommes. Cette approche, potentiellement plus fine, requiert que l'on sache mesurer l'intérêt pour la psychologie. C'est à la psychométrie de résoudre ce type de problème.

L'investigateur en psychologie a (au moins) quatre "casquettes" : psychologue, statisticien, enquêteur et psychométricien. En tant que psychologue, pour répondre à sa question de manière objective, il met la casquette de statisticien. En tant que statisticien, il demande à l'enquêteur de lui fournir des données. En tant qu'enquêteur, il demande au psychométricien de lui fournir des méthodes de mesure. Les casquettes de statisticien, enquêteur et psychométricien sont regroupées sous un seul chapeau, celui du méthodologue.
8. Questionnaire d'auto-évaluation
Ce QCM comprend 10 questions. Répondez à chaque question puis, à la fin, lorsque vous aurez répondu à toutes les questions, un bouton "terminer" apparaîtra sur la dernière question. En cliquant sur ce bouton, vous pourrez voir votre score et accéder à un corrigé.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte