Fréquence conditionnelle
Objectifs. Définir la notion de fréquence conditionnelle.
Prérequis.
Résumé. La notion de fréquence conditionnelle repose sur la donnée d'un couple de variables discrètes (X, Y). La fréquence d'une certaine valeur yj en Y conditionnellement à une certaine valeur xi en X est la proportion des cas de la classe xi qui ont pour valeur yj .
2. Couple de variables et notations
Le couple de variables ( X , Y ) est une application d'un ensemble d'êtres, ensemble noté généralement Ω, dans un ensemble d'objets qui sont des couples de valeurs descriptives. Cet ensemble est le produit cartésien de l'ensemble M( X ) des valeurs descriptives de la variable X et de l'ensemble M( Y ) des valeurs descriptives de la variable Y . Cet ensemble, qui s'appelle un référentiel de description (https://iris.univ-tlse2.fr/course/view.php?id=7873#section-5) est
M( X ) × M( Y ) = { x 1 , x 2 , ..., xi , ..., xp } × { y 1 , y 2 , ..., yj , ..., yq } = {( x 1 , y 1 ), ( x 1 , y 2 ), ..., ( x i , yj ), ..., ( xp , yq )}.
Les éléments du référentiel de description sont des objets conceptuels (des états). Ces objets se répartissent dans le tableau à double entrée associée au couple ( X , Y ) suivant :
| y 1 |
y
2
|
...
|
y i | ... |
y
q
|
|
| x 1 | ( x 1 , y 1 ) | ( x 1 , y 2 ) |
(
x
1
,
yj
)
|
(
x
1
,
yq
)
|
||
| x 2 | ( x 2 , y 1 ) | ( x 2 , y 2 ) | ( x 2 , yj ) |
(
x
2
,
yq
)
|
||
| ... |
|
|||||
|
xi
|
( xi , y 1 ) |
(
xi
,
y
2
)
|
( x i , yj ) | ( xi , yq ) | ||
| ... | ||||||
|
xp
|
( x p , y 1 ) |
(
x
p
,
y
2
)
|
(
x
p
,
yj
)
|
( x p , yq ) |
Explicitons les symboles utilisés dans ces notations :
- Les lettres x et y désignent des valeurs descriptives. Elles sont en minuscule pour ne pas confondre avec les lettres majuscules X et Y qui désignent des variables. Les valeurs descriptives sont numérotées. Ainsi, la variable X possède p valeurs, numérotées de 1 à p ; la lettre i indique la i ème valeur. Ces numéros sont ajoutés en indice de la lettre x , ce qui permet de désigner n'importe quelle valeur particulière de la variable X. Même raisonnement pour les lettres y de la variable Y qui possède q valeurs.
- Un couple est un ensemble ordonné : (X , Y) n'est pas la même chose que (Y , X) alors que {X , Y} = {Y , X}. On convient de ce que les lignes sont toujours réservées à la première variable du couple, et de ce que les colonnes sont toujours réservées à la seconde variable du couple (truc mnémotechnique : Li-Co pour ligne puis colonne).
- Les nombres ne sont jamais en italique. Les lettres sont en italique sauf exception cosmétique (par exemple Ω).
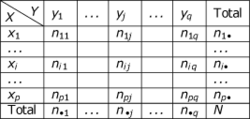
La table de contingence associée à (X , Y) est le même tableau, à la différence que les cellules du tableau contiennent le nombre des états -- ou objets -- (x , y) observés. Voici les notations associées :
| y 1 |
y
2
|
...
|
y i | ... |
y
q
|
||
| x 1 | n 11 | n 12 | n 1 j | n 1 q | n 1 • | ||
| x 2 | n 21 | n 22 | n 2 j |
n
1
q
|
n 2 • | ||
| ... |
|
||||||
|
xi
|
n i 1 | n i 2 | nij | niq | n i • | ||
| ... | |||||||
|
xp
|
n p 1 |
n
p
2
|
n
p
j
|
n p q | np • | ||
| n • 1 |
n
•
2
|
n
•
j
|
n
•
q
|
n
|
Par exemple, la notation n 12 désigne le nombre de fois où l'état (x1 , y2) a été observé dans Ω. C'est un effectif conjoint. La dernière ligne et la dernière colonne indiquent les effectifs marginaux. Par exemple, la notation n1 • indique le nombre de cas se trouvant dans l'état x1 ; le point qui suit l'indice 1 indique qu'on ne se soucie pas des valeurs prises par ces cas en Y.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte

