Statistique inférentielle et psychométrie appliquée

Idéalement, la décision statistique serait basée sur une évaluation du risque de se tromper si l'on rejetait l'hypothèse nulle, c'est-à-dire évaluer quelle est la probabilité de commettre l'erreur de type I. Mais cela, on ne le sait pas. Par contre, ce qu'on peut calculer c'est la probabilité -- en supposant l'hypothèse nulle vraie -- d'avoir les résultats qu'on a obtenus. Par exemple, reprenons l'exemple introductif de M. Magik qui lance trois fois la pièce sur pile ; comme il n'avait annoncé.

Par définition, on peut quantifier une probabilité comme étant le nombre de cas "favorables" (on devrait plutôt dire de "cas cibles", ce serait plus approprié dans les cas où l'on quantifie un risque d'erreur !) divisé par le nombre de cas possibles (ou le nombre de cas connus, si l'on évalue la probabilité empiriquement sur la base de faits connus). La probabilité d'obtenir par hasard un tel résultat (pile, pile, pile) sur 3 lancers est 1 sur 8 puisqu'il y avait huit possibilités de résultats. Donc la valeur p est ici 1/8 soit 0.125. Sous l'hypothèse nulle, il y avait 12.5% de chances d'obtenir un tel résultat. C'est moins d'une chance sur deux, mais cela reste en tout cas beaucoup trop élevé pour qu'on puisse affirmer qu'autre chose que le hasard a joué (que ce soit la pièce truquée ou un soi-disant pouvoir télékinétique). 

La majorité des tests que vous verrez en cours de statistique inférentielle dans la suite de votre cursus consisteront essentiellement en un ensemble de recettes plus ou moins sophistiquées pour calculer ces valeurs p, selon le type d'expériences, selon le type d'hypothèse nulle, selon la nature des données disponibles, etc.

Notons que formellement la valeur p est la probabilité d'obtenir nos données D sachant que l'hypothèse nulle est vraie, ce qu'on peut noter avec les conventions vues au lycée 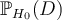$\mathbb{P}_{H_0}(D)$. En réalité, ce sont le chercheur aurait vraiment besoin pour sa décision, c'est la probabilité que l'hypothèse nulle soit vraie compte tenu des données disponibles, 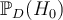$\mathbb{P}_D(H_0)$. Mais cela, attention, on ne l'a généralement pas !!

Mais alors, pourquoi nous intéresser à cette valeur p ? Parce que, intuitivement, plus ce nombre p est petit, et moins on a de chances de se tromper en rejetant l'hypothèse nulle. S'il y a une chance sur millle d'avoir un résultat comme on l'a eu si seul le hasard a joué, alors il devient difficile de croire que seul le hasard était à l'œuvre ! Bien sûr, cela reste néanmoins possible : même s'il y a moins d'une chance sur 1000 de gagner au loto, il y a pourtant régulièrement des gagnants. Cela nous amène à la question du seuil de la valeur p que l'on choisit comme acceptable ou non pour admettre un résultat scientifique comme valide...

Note : Vous pouvez aussi consulter notre article sur la façon de rédiger les valeurs p dans vos mémoires, devoirs, articles...