Statistique inférentielle et psychométrie appliquée
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L2 |
| Livre: | Statistique inférentielle et psychométrie appliquée |
| Imprimé par: | Visiteur anonyme |
| Date: | mardi 24 février 2026, 05:16 |
Description
 Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette leçon est essentielle pour comprendre les suivantes, car tous les concepts de base de la statistique inférentielle y sont expliqués.
Table des matières
- 1. Les étapes de la recherche scientifique
- 2. Mesurer ou décrire ?
- 3. La prédiction: scientifique ou actuarielle ?
- 4. Mesurage : logique et usage
- 5. Opérationnaliser une grandeur psychologique
- 6. Approche intuitive de la statistique inférentielle
- 7. L'hypothèse nulle
- 8. Population et échantillons
- 9. La décision statistique
- 9.1. On part de l'effet observé
- 9.2. Les causes de l'effet observé: hypothèse expérimentale et hypothèse nulle
- 9.3. Un pari pour ou contre l'hypothèse nulle
- 9.4. Les conséquences potentielles de la décision
- 9.5. Les risques de type I et II
- 9.6. Notion de "valeur-p"
- 9.7. Seuil de signification de la valeur p
- 10. Évaluer la valeur p
- 11. Questionnaire d'auto-évaluation
1. Les étapes de la recherche scientifique
Objectifs.
Replacer statistiques et mesurage dans le contexte général de la recherche.
Prérequis. Cours de L1
Résumé. On examine les étapes de la construction de connaissances générales à partir de données observables. La validité d’une connaissance dépend de la validité de chacune des étapes.
1.1. Le chercheur et le praticien
Le chercheur en sciences humaines, celui qui utilise quotidiennement la statistique et la psychométrie, le fait dans un objectif particulier : élaborer et valider des connaissances générales. Ces connaissances sont éventuellement utilisables ensuite par le praticien mais pas nécessairement. Le chercheur peut avoir un objectif de compréhension pure. Pour le chercheur, le raisonnement statistique est donc un outil conceptuel de première nécessité. Pour autant, la recherche est très loin de se limiter aux statistiques. Il convient donc de replacer la statistique et la psychométrie dans la perspective générale de la démarche de recherche scientifique.
La démarche du chercheur est très différente de celle du praticien qui, souvent, ne s'intéresse aux statistiques qu'en tant qu'aide au diagnostic, au sens où elles peuvent lui fournir des probabilités de pathologies associées à des configurations de symptômes (sachant que le patient a de la fièvre, qu'il tousse, qu'on est en hiver, les chances qu'il ait une grippe sont de ...), ou aide au pronostic (probabilités de guérison associées à des traitements). Mais même le praticien, pour pouvoir utiliser convenablement les statistiques que lui fournissent les chercheurs, doit au minimum comprendre ce que lui disent ces derniers. Il doit donc être capable de comprendre le langage des statistiques, c'est-à-dire savoir construire une représentation mentale valide des concepts véhiculés par le langage statistique.
1.2. La pyramide expérimentale
Norman Anderson a proposé « la pyramide expérimentale », un cadre conceptuel général pour décrire le raisonnement scientifique (Anderson, 2001), c'est-à-dire la construction de connaissances générales à partir de données observables. L’idée générale de cette pyramide est que les étapes de l’inférence scientifique constituent un tout dont les différents niveaux sont fondamentalement interdépendants. De ce fait, la validité d’une connaissance dépend de la validité de chacun des niveaux.
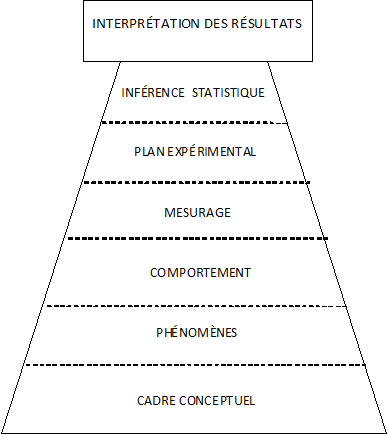
Nous allons maintenant détailler les différentes étapes, en montant du bas vers le haut de la pyramide.
Le cadre conceptuel
Un cadre conceptuel est un système de croyances interconnectées. Dans le domaine scientifique, on aime appeler ces croyances des « connaissances ». Ces croyances sont à des niveaux de généralité très divers et peuvent correspondre à de grands débats classiques (nature-culture, inné-acquis, etc.)
Dans toute étude scientifique, le cadre conceptuel est premier. Il peut être très fruste, comme lorsque l’on démarre une recherche sur un sujet qui n’a jamais été étudié, ou au contraire s’appuyer sur des centaines d’années d’élaborations théoriques étayées d’observations empiriques. Mais même dans sa version la plus simple, le cadre conceptuel contient des assomptions sur les phénomènes qu’il est pertinent d’étudier ou non, ou sur les aspects d’un phénomène qu'il serait plus pertinent d’étudier. Par exemple, pendant la période béhavioriste, et pour les chercheurs appartenant à cette mouvance, il n’était pas considéré comme pertinent d’étudier autre chose que des comportements observables. Avec l’arrivée du cognitivisme, les chercheurs en psychologie expérimentale ont réintroduit la possibilité de faire appel, au moins partiellement, aux contenus des données verbales. Le changement de cadre conceptuel se traduit donc par des changements méthodologiques et même, plus profondément, par des changements d'objet d'étude. En fait, le cadre conceptuel peut contenir des croyances sur la totalité des éléments d’une recherche, voire sur la nature même de la recherche en général.
Le phénomène
Un travers de la recherche, lorsque l'on commence l'investigation dans un nouveau domaine, est de confondre ce que l'on observe et ce que l'on cherche à observer. Ainsi, les premiers chercheurs en psychologie, au XIX e siècle, utilisaient l'introspection et tenaient ce que disaient les sujets pour des traces fiables de ce qui se passait dans leur tête. On a fini par s'apercevoir de l'impasse que constituait une perspective aussi naïve et les techniques d'investigation des processus mentaux ont permis de montrer que la représentation qu'un sujet se construit de ses propres processus mentaux, et donc ce qu'il en raconte, peut n'avoir rien à voir avec la réalité de ces processus. Dans la terminologie d’Anderson, le "phénomène" correspond à la chose que l’on cherche à connaître, mais qui, pour toutes sortes de raisons, peut n’être pas directement le comportement que l’on va observer.
Les raisons qui imposent de distinguer le phénomène de la chose à observer incluent notamment les variables parasites, c’est-à-dire des éléments qui viennent perturber le comportement produit par les sujets de sorte qu’en observant le comportement, on n’observe pas le phénomène cible, mais une sorte de mélange du phénomène cible et de la variable perturbatrice. Par exemple, l’expérimentateur qui donne une consigne à un sujet suppose que le comportement résultant traduira le phénomène qu’il étudie. Mais le sujet doit d’abord interpréter la consigne. Des variations dans l’interprétation de la consigne donnée, pour des raisons purement linguistiques par exemple, peuvent conduire à des variations subséquentes du comportement du sujet. Ces variations n’ont rien à voir avec le phénomène étudié par le chercheur.
La couverture du phénomène est aussi affectée par le choix des tâches expérimentales. Certaines peuvent bien cibler un aspect du phénomène mais pas sa totalité, de sorte que les résultats obtenus, même s’ils sont valables, ne se généraliseront pas lorsque la recherche portera sur des tâches légèrement différentes. Certaines tâches expérimentales donnent des résultats qui se généralisent bien, d’autres non.
Les comportements
Dans un cadre expérimental, le comportement du sujet provient d’une interaction entre les caractéristiques propres du sujet et les caractéristiques de la situation construite par l’expérimentateur, et à laquelle le sujet semble avoir accepté de se soumettre.
Sur des études où le chercheur prend le parti d’être moins intrusif, le sujet peut être observé dans une situation qui lui est plus naturelle, c’est-à-dire qui n’a pas été véritablement construite par l’expérimentateur. Bien entendu, il ne s’agit pas d’être naïf et oublier que même dans ces situations, le chercheur a quand même une influence sur les observations, ne serait-ce qu’en choisissant d’observer tel comportement plutôt que tel autre, sous tel angle plutôt que tel autre, etc. De ce fait, l’interprétation ultérieure des données produites devra tenir compte, autant que faire se peut, des choix ayant présidé à l’observation.
Les choix méthodologiques constitutifs de l’observation du comportement font l’objet de controverses scientifiques, car il est toujours possible, face à un résultat dérangeant, de mettre en cause le dispositif de recueil des données plutôt que la théorie testée. D’un autre côté, la théorie sur le fonctionnement de la réalité observée vient déterminer les choix méthodologiques eux-mêmes, de sorte qu’il est quasiment impossible d’obtenir des observations « pures ».
Le mesurage
C’est l'étape cruciale par laquelle des données empiriques observables sont codées numériquement.
Deux concepts sont essentiels pour le mesurage : la validité et la fidélité. La fidélité traduit la capacité de la mesure d’être répliquée. Une mesure porte donc d’autant plus de contenu informationnel qu’elle est fidèle, car les parties de la mesure qui ne se répliquent pas d’une expérience sur l’autre ne sont pas véritablement porteuses d’information. En y regardant de plus près, la notion de fidélité n'est pas équivalente à celle de précision, mais ici, en première approximation, on peut se contenter de garder l'idée générale que ces deux notions à peu près équivalentes : plus une technique de mesurage produit des mesures précises, plus grande sera la fidélité des variables étudiées (voir aussi l'article de L1 sur la
précision des tests). La validité est un concept très complexe qui mériterait plusieurs articles à lui seul (voir par exemple l'article de L1 sur la
validité des tests).
Le plan expérimental
Le plan expérimental a pour premier effet de permettre au chercheur de parler en termes de causalité. En effet, selon le plan expérimental, le chercheur pourra simplement établir des relations entre des variables (observer que telle et telle variables tendent à marcher ensemble) ou au contraire il pourra aller plus loin et parler de causalité, c'est-à-dire qu'il sera en mesure de dire que telle variable CAUSE telle autre. Opérationnellement, cela signifie que si l'on intervient sur les valeurs d'une variable cause, aussi appelée « variable indépendante », il devrait s'ensuivre une modification des valeurs de l'autre variable, la variable effet, dite aussi « variable dépendante ».
Dans une recherche expérimentale, un plan expérimental bien conçu permet aussi de contrôler l'effet de variables parasites que l’on n’a même pas pu identifier.
Au-delà, et d'une manière qui concerne plus directement le contenu de ce cours, le plan expérimental détermine comment les données seront traitées statistiquement. Par suite, il détermine quelle sera la « puissance statistique » du test, c’est-à-dire qu'il détermine la capacité du test à détecter un effet significatif si un tel effet existe réellement.
L’inférence statistique
Ce niveau correspond usuellement à la production de la fameuse valeur « p » qui indique si le test est « significatif » ou non. Malgré son succès dans la communauté scientifique, c’est peut-être le niveau le moins important. Et si l’élément le plus populaire au sein de ce niveau, le test de signification, est certes nécessaire, car il permet de décider si l'on peut considérer les données comme autre chose qu'un pur coup de chance ou de malchance, usuellement, trop d’importance lui est accordée.
L'attrait de cette valeur de signification est tel que des débutants se précipitent très souvent pour rapporter le fait qu'un test est significatif en omettant de rapporter le résultat lui-même : on a un résultat « statistiquement significatif ». Très bien ! Mais... qu'est-ce qui est significatif ? Quel est ce résultat qui est significatif ?
D’autres éléments, auxquels on accorde habituellement moins d’importance, sont en fait plus informatifs. Ainsi en est-il des notions d’intervalles de confiance ou de tailles d’effet.
L’interprétation des résultats
Cela correspond à la partie « discussion » des articles scientifiques et ne fait pas spécifiquement partie de l'objet du présent cours.
3. CONCLUSION
La statistique et le mesurage constituent des moments d'une démarche globale et doivent donc être considérés dans le cadre général de cette démarche, c'est-à-dire que les méthodes employées et la qualité des résultats qu'ils produisent sont toujours à envisager relativement à l'objectif général de la recherche dans laquelle ils prennent place.
2. Mesurer ou décrire ?
Objectifs. Introduire la problématique du mesurage en psychologie comme cas particulier de la description scientifique.
Prérequis. Aucun.
Résumé. La psychologie sera une discipline scientifique générale si ses connaissances sont objectives et générales. L'objectivité est définie selon un critère d'interchangeabilité des observateurs lorsqu'ils décrivent un phénomène particulier. Lorsque la description prend la forme d'un nombre ou d'un intervalle de nombres, c'est que le phénomène est conçu, implicitement ou explicitement, comme un phénomène ordinal ou quantitatif.
2.1. L'objectivité des descriptions psychologiques
Dans la mesure où la psychologie aspire à être une science empirique, c'est-à-dire une science des êtres réels dotés d'une psychologie, son problème préliminaire consiste à décrire les êtres du point de vue auquel elle s'intéresse. En effet, une psychologie qui admettrait d'entrée de jeu que les phénomènes psychologiques sont indescriptibles se condamnerait à être une science mort-née. La constitution d'un domaine de description des êtres psychologiques (i.e., dotés d'une psychologie) présente plusieurs problèmes, à commencer par celui de l' objectivité de ses descriptions.
Savoir si une description est objective est une question épineuse. Si je dis que Paul est très intelligent par exemple, on peut se demander si Paul est réellement très intelligent, c'est-à-dire mettre en doute la correspondance entre ce qu'énonce ma description et l'intelligence de Paul. Ou bien j'admets que l'intelligence très élevée de Paul existe indépendamment de l'appréhension que je peux en avoir, auquel cas l'intelligence de Paul est postulée comme un phénomène qui a sa propre ontologie (ou encore sa propre existence), ou bien je considère que l'intelligence de Paul est essentiellement le résultat de mon regard sur Paul, c'est-à-dire que si personne ne s'intéresse à Paul, son intelligence n'existe pas. Dans le premier cas, l'intelligence de Paul est une propriété psychologique à laquelle on attribue une ontologie intrinsèque, tandis que dans le second cas, l'intelligence de Paul consiste en un jugement qui confère à Paul le statut social de quelqu'un qui possède un certain nombre de capacités, indépendamment de ce que Paul peut effectivement faire. Et ce jugement peut être objectif ou subjectif. Il est subjectif s'il dépend de moi, en ce sens que Brigitte ne trouve pas que Paul est très intelligent. Il est objectif si Brigitte et n'importe qui d'autre, y compris Paul, trouve que Paul est très intelligent. Cette réflexion préliminaire est inspirée par l'ouvrage de John R. Searle qui s'intitule The construction of social reality.
Cette analyse met en évidence que la question de l'objectivité des descriptions psychologiques comporte au moins deux problèmes :
- le problème ontologique (l'intelligence de Paul a-t-elle une existence propre ?),
- le problème de l'objectivité épistémique (l'intelligence de Paul est-elle une propriété qui peut être attestée publiquement ?).
Il se peut que les tests psychologiques soient un moyen de décrire avec objectivité (épistémique) des réalités construites socialement, c'est-à-dire qui n'ont pas d'autre ontologie que celle que leur confère une communauté sociale. La psychologie est une discipline éminemment ambigüe quant à ses objectifs : s'agit-il de déterminer des individus dans une grille essentiellement fonctionnelle en fonction des besoins pragmatiques des situations (recrutement, soins, qualification, etc.), ou bien d'identifier des contraintes (lois) régissant le cours de phénomènes psychologiques possédant leur propre ontologie ?
Il demeure que je suis un juge, c'est-à-dire que ma proposition descriptive, "Paul est très intelligent", engage mes capacités sensibles et intellectuelles vis-à-vis de la communauté des êtres qui parlent le langage descriptif que j'utilise. Pour évaluer l'objectivité de mon jugement, la seule chose que je peux faire est de recourir au témoignage des autres concernant l'intelligence de Paul, ne serait-ce qu'en pensée. Il ne s'agit pas d'objectivité au sens de la postulation de l'ontologie d'une propriété intrinsèque, mais d'objectivité au sens de l'interchangeabilité des juges (objectivité épistémique). Que plusieurs juges s'accordent exactement sur l'état psychologique d'un être étant donnés l'expérience (intime) qu'ils en ont et un certain langage de description qu'ils partagent n'est pas un fait trivial : c'est que ce langage est capable de déterminer quelque chose de l'être qu'il s'agit de décrire, de telle manière que je pourrai faire confiance à n'importe quel témoin, puisque ce témoin fonctionne comme moi-même quand il fait l'expérience de l'être auquel je m'intéresse, et que n'importe qui pourra aussi me faire confiance si je suis le témoin de cet être, puisque je fonctionne comme lui-même.
Si nous sommes trois à avoir rencontré Paul aujourd'hui, nous pouvons séparément répondre à la question suivante :
Paul est très intelligent :
- vrai
- faux
- je ne sais pas.
La solution que nous proposons pour établir non pas la réalité de la description, mais son objectivité épistémique, est la suivante : il suffit de l'unanimité sur "vrai" d'un comité de juges qualifiés, c'est-à-dire, ici, de personnes (i) parlant le même langage descriptif, (ii) ayant rencontré Paul aujourd'hui, ou vu un enregistrement de Paul aujourd'hui. Faute d'accès à l'état réel de Paul, on utilise l'unanimité quant à la vérité d'une proposition comme forme spéciale d'intersubjectivité. Le jugement de vérité ne porte pas sur l'état réel de Paul. Il s'appuie sur l'expérience subjective de l'état de Paul par des êtres faillibles et limités, dont on utilise les capacités cognitives à juger de la vérité de la proposition descriptive. Ce qui est vrai ou faux n'est pas un état réel, mais une description intersubjective.
La vérité d'une description n'est pas absolue, puisqu'elle dépend du comité (réel et en pratique imaginaire) dont on invoque la belle unanimité. L'objectivité scientifique d'une proposition descriptive signifie que sa valeur de vérité dépend non spécifiquement de celui qui l'énonce, le juge étant par principe interchangeable avec n'importe quel autre juge. Les descriptions objectives correspondent à ce que Popper, dans La logique de la découverte scientifique, appelle des "propositions ou énoncés de base" ("basic statements").
Une fois qu'on s'est mis d'accord sur l'objectivité des descriptions psychologiques, c'est-à-dire qu'on a convenu de ce qu'une description est objective si on peut montrer qu'un jury quelconque est unanime sur sa vérité, on dispose d'un critère pour valider un langage descriptif : un langage descriptif est un langage qui permet des descriptions objectives. Le problème qui surgit immédiatement est qu'un adjectif comme "intelligent" ne permet pas de description objective. En effet, il sera difficile à quiconque dans un tel comité de ne jamais utiliser l'option de réponse "je ne sais pas" ; ce type d'expérience conduite dans un amphithéâtre de psychologie montre facilement qu'il existe de nombreuses situations de non-unanimité. Nous touchons ici un point conflictuel en psychologie. Par exemple, les psychologues qui utilisent les tests projectifs, ou les descriptions du DSM par exemple, ne sont pas intransigeants quant à l'objectivité des descriptions afférentes à ces cadres descriptifs. Si les descriptions dépendent spécifiquement des juges, le processus d'objectivation produit une variabilité nuisible à la connaissance scientifique des êtres psychologiques, puisque cette variété ne dépend par principe pas des êtres décrits, mais des êtres descripteurs. À nos yeux, ce problème n'est pas convenablement réglé dans de nombreux champs de la psychologie.
2.2. Décrire pour chercher des faits généraux

L'application du critère de l'objectivité des descriptions a une conséquence constitutive : la description littéraire d'un être psychologique n'est pas une description scientifique parce qu'elle n'est pas objective. Prenons par exemple la description d'Emma Bovary par Flaubert : eh bien la psychologie scientifique doit s'en passer, malgré sa richesse, sa profondeur, bref, malgré la merveilleuse véridicité à laquelle elle nous permet d'accéder. La description littéraire n'entre pas dans le projet de la connaissance scientifique parce que ce qui est visé est une connaissance générale des êtres psychologiques (cf. l'article Les étapes de la recherche scientifique). Plus précisément, il s'agit de dégager de l'infinie variation des cas particuliers des phénomènes généraux, autrement dit des lois empiriques.
Une loi empirique repose sur une structure descriptive simple : d'un côté, on décrit les êtres psychologiques d'après un ensemble d'états initiaux possibles (actualisés ou non actualisés), et un ensemble d'états dont l'actualisation dépend par hypothèse de celle des premiers. Par exemple, on demande à un adulte quelconque de lire à voix haute une liste de 20 mots et, dès qu'il a terminé, de dire quels sont les mots dont il se souvient. Par construction, l'état initial de cet adulte est "a lu les 20 mots" (par opposition a "n'a pas lu les 20 mots"). L'état "final" est "a rappelé les 20 mots" ou "n'a pas rappelé les 20 mots". La loi empirique peut se formuler de la manière suivante :
Quel que soit un adulte, s'il a lu les 20 mots il ne rappellera pas les 20 mots (sans aide extérieure).
BIen entendu, cette loi peut être fausse. Toutes les lois empiriques peuvent être fausses. Des observations générales analogues conduisent à l'idée que la mémoire immédiate est limitée, d'où la recherche d'explications. Autrement dit, la description scientifique n'a pas de finalité artistique. C'est une description orientée par la recherche de faits généraux, qui deviendront ensuite des faits à expliquer, qui conduiront peut-être à de nouvelles observations tirant leur sens de ces tentatives d'explication.
Lorsqu'un fait général est corroboré de nombreuses fois, on finit par s'y habituer. Par exemple, vous vous tenez debout et vous lâchez par inadvertance votre tasse de café fumant. Votre tasse se tient bien tranquillement dans la position spatiale où vous l'avez lâchée, alors que l'habitude vient de vous faire sauter en arrière pour éviter les éclaboussures. Un physicien qui montre qu'il est possible de lâcher son café dans ces conditions aura sans doute beaucoup de facilité à trouver un poste, parce qu'il vient de découvrir que la gravité n'est pas aussi générale que ce qu'on croyait. Il aura découvert des conditions pour lesquelles cette loi ne s'applique pas. En psychologie, les descriptions objectives sont en principe intéressantes si elles falsifient des faits généraux bien admis. Par exemple, le psychologue qui parvient à former n'importe quel adulte à se rappeler les 20 mots de la liste se trouverait dans des conditions analogues à celles de notre physicien pour obtenir un poste ou des financements. (Un de nos collègues a récemment attiré notre attention sur l'hypermnésie : il paraît qu'il existe des gens capables de se rappeler une liste de 20 mots dans les conditions expérimentales que nous avons décrites plus haut : comment font-ils ?)
Il faut décrire objectivement pour qu'il soit possible de découvrir ou d'énoncer des faits généraux. Il faut des faits généraux pour qu'il soit possible de découvrir ou d'énoncer des faits singuliers qui les dénoncent, et qui stimuleront la recherche d'explications, c'est-à-dire la recherche des conditions spéciales qui autorisent ce que la loi interdit -- la loi étant la généralisation du fait général, notamment au futur.
2.3. Mesurer c'est décrire une grandeur
Dans ce qui précède, nous n'avons pas eu besoin d'identifier la description à la quantification. Pourtant, en psychologie, on accorde une grande importance à la quantification, pour des raisons complexes. Nous ne prétendrons pas analyser ici ces raisons, mais nous pointerons une interprétation possible : la plupart des grandeurs qui intéressent les psychologues sont des métaphores du langage de la vie quotidienne. Par exemple, on parle de la capacité de la mémoire immédiate comme d'une grandeur : il y a des gens plus ou moins capables, donc il s'agit de mesurer cette capacité. Ce type de démarche s'oppose à une démarche qui part du principe que c'est une question empirique (et non de droit) de savoir si l'idée d'une grandeur latente, i.e., non observable, correspond à une réalité dont l'ontologie est intrinsèque. Les psychologues ont l'habitude de considérer qu'il est normal de mesurer des grandeurs non empiriques par des procédés numérologiques (cf. l'article "Score psychométrique" de L1) et nous ne partageons pas cette position parce qu'elle n'est pas justifiable dans une perspective réaliste (i.e., dans une perspective qui assigne comme but à la recherche scientifique la connaissance de la réalité telle qu'elle existe indépendamment du sujet de la connaissance, par opposition à des productions linguistiques partagées -- dont Searle nous montre qu'il faut bien, par ailleurs, reconnaître l'ontologie sociale ou encore subjective).
Par définition, ce qui est mesurable est une grandeur ; les grandeurs physiques sont des concepts fondés sur des réseaux de connaissances empiriques complexes. Un ampèremètre mesure l'intensité dans un circuit électrique, pas seulement parce que nous souhaitons collectivement que l'intensité soit mesurée, mais en vertu de la capacité de l'instrument à résumer les faits empiriques généraux qui permettent de définir l'intensité du courant électrique comme une grandeur. Ceci ne signifie pas qu'il faille s'interdire d'utiliser des métaphores si on fait de la recherche scientifique, mais qu'il faut s'interdire de prendre ces métaphores pour des propriétés intrinsèques (réification). Nous renvoyons le lecteur au chapitre plus bas "Opérationnaliser une grandeur psychologique ".
2.4. Bricolages psychotechniques pour décideurs dans le brouillard
La psychologie s'est développée sous un régime historique particulier : avant même qu'elle n'atteigne sa maturité, il a fallu qu'elle rende service. D'où l'immense développement des méthodes psychotechniques, qui reposent pour l'essentiel sur une procédure d'observation standardisée couplée à une règle de projection des observations sur une échelle de scores. C'est ainsi que les psychologues ont pris l'habitude d'utiliser les tests psychologiques pour étayer des décisions incertaines. Nous renvoyons le lecteur à l'article "Applications de la psychométrie" pour un aperçu. Le fait d'éduquer systématiquement les psychologues à manipuler des scores a un corollaire : ils sont systématiquement éduqués à ne pas réfléchir à la manière dont on construit les descriptions qui sont nécessaires à la numérologie psychométrique - c'est-à-dire la fabrication de scores à partir d'étiquettes numériques codant des réponses qualitatives (voir l'article de L1 "Score psychométrique"). L'article "Algèbre d'événements" aborde ce point en détail.
L'article suivant développe le problème de la prédiction scientifique, dont la maîtrise est un préalable à la maîtrise des techniques inductives qui utilisent les scores psychométriques comme support d'inférence.
3. La prédiction: scientifique ou actuarielle ?

Objectifs . Poser le problème de la prédiction scientifique.
Prérequis. Aucun.
Résumé. La prévision est présentée selon deux perspectives : soit on dispose de règles générales, auquel cas il s'agit de prévision scientifique parce que ces règles sont falsifiables par chaque prévision, soit on ne dispose pas de règles générales et on peut alors s'appuyer sur l'hypothèse que les phénomènes auxquels on s'intéresse obéissent à une loi de probabilité. Mais alors la prévision d'un événement singulier n'a pas de fondement, et on peut seulement espérer en tirer profit en termes de multitudes de prédictions.
3.1. Le problème
Prédire un comportement consiste à se projeter dans le futur, c'est-à-dire à s'aventurer dans l'inconnu armé de conjectures. Il y a des conjectures qui, a posteriori, s'avèrent fondées, d'autres non, et d'autres qui ne peuvent pas être vérifiées (par exemple, il est probable que vous rencontriez l'amour de votre vie demain). La prévision scientifique est un art de la divination qui se fonde sur l'exigence de falsifiabilité de ses prévisions, et l'élimination des croyances qui s'avèrent fausses précisément parce qu'elles ont conduit à de fausses prévisions.
La notion de falsifiabilité demande quelques explications. Par exemple, prédire que "demain le ciel sera sans nuage" est une prédiction falsifiable : soit il n'y aura pas de nuage, auquel cas la proposition sera vérifiée, soit il y aura au moins un nuage, auquel cas la proposition sera falsifiée. Mais énoncer qu'il y a 9 chances sur 10 que le ciel soit sans nuage demain n'est pas une proposition scientifique parce qu'elle est tautologique : elle implique logiquement que, soit il y aura au moins un nuage, soit il n'y en aura pas. Le recours à la probabilité d'un événement singulier se fonde sur des modèles peut-être scientifiques (i.e., falsifiables, et alors, il s'agit de préciser en quoi ils sont falsifiables en jugeant sur pièces), mais cela ne suffit pas pour faire de ce type d'énoncés des énoncés scientifiques.
La notion de prédiction scientifique est très clairement définie par Popper (1973) : "Pour prévoir, il est besoin de lois et de conditions initiales ; si l'on ne dispose pas de lois ou si l'on ne peut constater de conditions initiales, il ne s'agit plus de prévisions scientifiques" (p. 207). Dans l'article précédent, nous avons développé la notion de fait général (voir aussi Vautier, 2011 en VF). Dans ce qui suit, nous présentons de manière critique l'approche actuarielle de la prévision.
3.2. Prévision actuarielle d'un événement singulier
La prévision actuarielle consiste à utiliser la fréquence des événements pour une prévision probabiliste (i.e., infalsifiable par l'observation de l'événement en question, mais testable en théorie sur une série de prévisions). Nous allons utiliser un exemple proposé par Lee J. Cronbach dans son ouvrage intitulé "Essentials of psychological testing" (1990, voir aussi notre article du cours de L1 "Un test psychométrique est-il valide ?").
Cronbach utilise les données suivantes :
| D | C |
B
|
A
|
|
|
41-50
|
99
|
92
|
62
|
21
|
| 31-40 |
98
|
82
|
42
|
10
|
|
21-30
|
94
|
66
|
25
|
4
|
|
11-20
|
85
|
47
|
12
|
1 |
|
1-10
|
71
|
29
|
5
|
<1
|
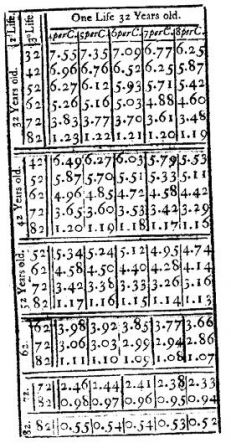
Les intervalles de valeurs de la première colonne indiquent la somme des scores obtenus à deux tests d'aptitude (raisonnement arithmétique, perception spatiale). Les scores proviennent de lycéens inscrits dans 25 lycées (les données sont en fait empruntées à une étude plus ancienne et les détails ne sont pas communiqués). Les lettres A à D indiquent des grades, c'est-à-dire des niveaux d'évaluation en dessin industriel (notre traduction de "drafting") : le meilleur grade est le grade A.
Les nombres contenus dans les cellules sont des pourcentages cumulés : par exemple, parmi les lycéens ayant un score compris entre 41 et 50 points, 21% ont obtenu le grade A, 62% ont obtenu au moins le grade B, 92% ont obtenu au moins le grade C, etc.
Cronbach évoque un conseiller qui devrait diriger l'attention du lycéen qu'il conseille, et qui a obtenu 25 points, sur la ligne de la table indiquant "qu'il a deux chances sur trois d'obtenir au moins le grade C" (p. 153). Que signifie cette proposition ? D'un point de vue factuel, 66% des lycéens de l'échantillon qui ont obtenu un score compris entre 21 et 30 points ont au moins le grade C. Il s'agit d'une fréquence conditionnelle. L'interprétation que Cronbach suggère au conseiller de suggérer au lycéen qui est venu le consulter n'est pas la même. Elle repose sur la notion de chance d'obtenir au moins le grade C.
La notion selon laquelle un événement a une chance parmi n ( n étant un nombre naturel non nul) de se réaliser est une notion obscure sinon obscurantiste. Il s'agit d'invoquer le hasard, ou encore une force occulte qui régirait le cours des événements. Ce que nous savons logiquement est (i) qu'il existe une possibilité sur deux pour que l'événement se réalise, et (ii) que nous ignorons si cet événement se réalisera. En fait, l'interprétation probabiliste de Cronbach est un aveu d'ignorance du conseiller. Mais alors, à quoi sert le conseiller ?
Le conseiller a deux choix : soit il se drape dans le rôle de divinateur savant (parce que l'actuariat, c'est une affaire de savants), soit il refuse d'endosser ce rôle. Si le lycéen cherche un gourou, le premier choix correspond à une logique de satisfaction de la demande. Si, de surcroît, le conseiller est payé pour faire de la satisfaction, son choix est rationnel, parce que s'il produit de l'insatisfaction il sera rapidement remercié par l'institution qui l'emploie, pourvu que ladite institution dispose des moyens juridiques de définir l'insatisfaction des clients comme une faute professionnelle. Si le lycéen cherche de l'information, alors le second choix est approprié et il n'est pas nécessaire d'utiliser le langage de la prédiction d'un événement futur.
L'obtention du grade "au moins C" dépend de toutes sortes de circonstances qui échappent à la façon dont Cronbach envisage le conseil dans le paragraphe qui nous intéresse. Le lycéen peut apprendre des données que parmi les lycéens de sa catégorie (i.e., ceux qui ont obtenu un score compris entre 21 et 30 points), tout est possible en matière de grade. Il peut donc supposer que présentement, rien ne l'empêche d'obtenir tout grade. En fait, les données indiquent que le score psychotechnique ne permet pas de faire l'hypothèse qu'il existe des scores interdisant l'obtention de n'importe quel grade ; en d'autres termes, les données ne révèlent aucun fait général. Il est alors tentant d'en déduire que la connaissance du score aux tests ne sert à rien : le conseiller pourrait indiquer à un lycéen inquiet parce qu'il a obtenu un score très faible que rien dans les données dont il dispose ne permet d'exclure qu'il pourrait obtenir le meilleur grade. Quant à la question de savoir ce qui déterminerait l'obtention d'un grade particulier, les données ne sont pas pertinentes.
3.3. Prévision actuarielle d'un événement collectif
La prévision actuarielle n'est pas destinée à la prévision d'événements singuliers, mais à la prévision d'événements collectifs. Un événement collectif réfère à une classe d'événements, ou encore, et peut-être plus exactement, à une classe de référence. Continuons avec l'exemple de Cronbach, en procédant en deux temps : d'abord de manière rétrospective, puis de manière prospective.
Si on considère les lycéens qui ont obtenu un score entre 41 et 50 points par exemple, quel est le pourcentage conditionnel (i.e., conditionnellement à la classe [41, 50]) de chaque grade ?
- 21% pour le grade A,
- 62 - 21 = 41% pour le grade B,
- 92 - 62 = 30% pour le grade C,
- 99 - 92 = 7% pour le grade D,
ce qui donne un total de 99% logiquement impossible. Les erreurs d'arrondi expliquent peut-être cette bizarrerie et nous considérerons que 8% des étudiants de cette classe ont le grade D.
Maintenant, expérimentons. On tire au sort un des lycéens de la classe et on note son grade dans le tableau suivant :
|
Tirage
|
A | B |
C
|
D
|
| 1 |
0
|
0
|
1
|
0
|
|
2
|
0
|
0
|
0
|
1
|
|
3
|
0
|
0
|
0
|
1
|
|
...
|
|
|
||
|
n
|
|
|
|
|
On obtient un lycéen qui a le grade C. On repose le nom de ce lycéen dans son urne et on recommence, pour obtenir cette fois un lycéen de type D. On repose le nom de ce lycéen et on recommence, avec le même résultat. On peut recommencer nos observations jusqu'à en avoir, par exemple, n = 2000.
On calcule alors la fréquence de chaque événement (A, B, C ou D) lorsqu'on a fait un tirage, deux tirages, trois tirages, etc. jusqu'à n tirages, et on affiche les résultats sur le graphique ci-dessous.
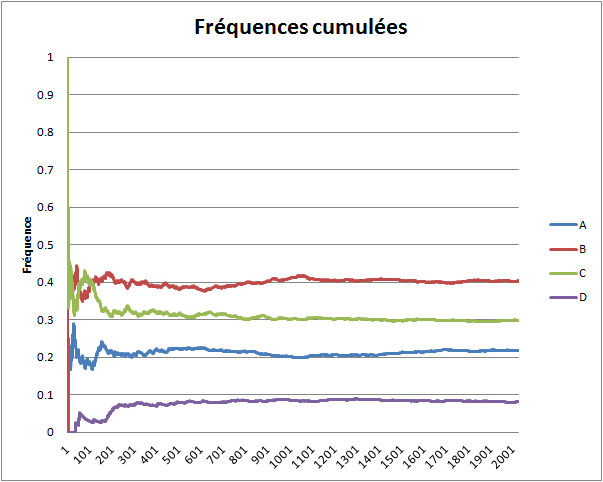
Le phénomène remarquable est la convergence de chaque série de fréquences. La série des fréquences de l'événement A converge vers la valeur de la probabilité de l'événement A, la série des fréquences de l'événement B converge vers la valeur de la probabilité de B, etc. Si on recommence toute l'expérience, on obtiendra des courbes (très probablement) différentes, mais ces courbes convergeront encore vers la valeur de la probabilité de l'événement auquel elles sont associées. Pour expérimenter par vous-mêmes à l'aide d'un simulateur informatique, cliquez ici. La théorie des probabilités explique logiquement cette nécessité.
Maintenant, tournons-nous vers l'utilisation prospective des données. En effet, les résultats que nous venons d'expliquer reposent sur la donnée de l'échantillon des lycéens, qui permet de connaître la proportion de chaque événement sur laquelle se fonde la convergence. La prévision actuarielle d'un phénomène porte sur la fréquence dudit phénomène (ou événement) -- c'est pourquoi nous parlons d'événement collectif -- et s'applique à des événements futurs. Le problème qui se pose est de savoir si la fréquence converge. Question purement métaphysique, puisqu'on ne connaît pas ladite population et donc pas la proportion des événements.
On décide alors de croire en la convergence. Muni de cette hypothèse, on peut supposer que la fréquence de A dans des échantillons de nouveaux lycéens qui ont un score entre 41 et 50 points tend vers une certaine valeur, pas forcément voisine de .21, au fur et à mesure qu'on augmente la taille de ces échantillons. Si je dois optimiser le nombre de fois où j'ai raison en prédisant un grade, je peux donc prévoir systématiquement le grade B compte tenu de ce que je connais, pourvu que j'aie affaire à un grand nombre de décisions (regardez sur les courbes combien d'observation sont nécessaires pour que les courbes ne se croisent plus). S'il s'avérait que les courbes de fréquences de très gros échantillons ne soient pas convergentes, il faudrait en déduire que le recours à la notion de loi de probabilité (i.e., l'idée que les proportions dans la population sont fixes) n'est pas fondé.
Ce type de raisonnement est utilisé par les assurances qui ajustent leurs tarifs en fonction des types de clients. Par exemple, on peut s'intéresser à la fréquence des accidents de la route en fonction du sexe et de l'âge des conducteurs, pour appliquer des tarifs avantageux aux clients appartenant aux classes les plus sûres si ces clients ne veulent pas être solidaires des clients des classes les moins sûres (ici, le lecteur aura compris que nous ne connaissons pas grand-chose en matière de politique tarifaire des assurances).
3.4. Conclusion
La notion de prévision est polysémique. Nous avons distingué la prévision scientifique, fondée sur une loi (ou encore un fait général) de la prévision actuarielle, fondée sur une loi de probabilité supposée gouverner la fréquence avec laquelle une classe d'événements se réalise.
Le psychologue intéressé par le conseil individuel se trouve dans une situation embarrassante s'il ne dispose pas de faits généraux ou s'il est consulté pour des choix ponctuels. Il serait alors bien avisé de ne pas invoquer des lois de probabilité occultes et de centrer son intervention sur l'affirmation de ce que ces données lui disent en termes de possibilités.
Le psychologue intéressé par les phénomènes de masse a tout intérêt à collecter des observations de manière à disposer d'une appréciation sensible des fréquences à l'aide de courbes de fréquences. En particulier, rien n'exclut que des tendances évoluent.
4. Mesurage : logique et usage

Objectifs Analyser le rôle du mesurage dans la recherche psychologique.
Prérequis.
Résumé. Cet article a pour objectif d'identifier, à partir d'un exemple, les erreurs logiques qui sous-tendent l'utilisation des scores comme mesures de grandeurs psychologiques.
4.1. Introduction
Le terme "mesurage" désigne l'action de mesurer. Du point de vue grammatical, le verbe "mesurer" est un verbe transitif direct, c'est-à-dire qu'il appelle un complément d'objet direct. Autrement dit, si on dit "je mesure", il faut compléter la phrase en indiquant ce qui est mesuré. Du point de vue sémantique, ce qui est mesuré est par définition une grandeur. Par exemple, si je dis "je mesure la taille de Paul", la taille de Paul est une grandeur.
En psychologie, le verbe "mesurer" est largement utilisé. Le problème qui nous intéresse ici est de savoir si cet usage est logiquement cohérent. Par exemple, si l'usage en psychologie est qu'on mesure l'attachement d'une personne à son quartier, alors le fait de se demander si cette personne est plus attachée à son quartier aujourd'hui qu'il y a trois ans entre en droit dans le cadre de l'activité du psychologue. Mais pour que cet usage puisse se prévaloir de la scientificité, il faut encore qu'il ne souffre pas d'incohérence logique.
Le problème général que posent l'usage et l'enseignement du mesurage en psychologie est qu'il existe de sérieux problèmes de cohérence logique. De plus, ces problèmes ne sont pas appréhendés correctement parce que l'enseignement méthodologique en psychologie néglige généralement de poser le problème philosophique du rôle de la rationalité dans la démarche scientifique. Or, dans les sciences empiriques, la connaissance repose sur l'exercice de la raison et sur l'observation. Lorsque le mesurage, qui est une forme particulière de l'observation, repose sur des conventions irrationnelles ou encore illogiques, son utilisation s'expose au risque de fraude (Atlan, 2010), c'est-à-dire d'une affirmation délibérée de pseudo-vérités scientifiques. Une parade obscurantiste à l'accusation de fraude scientifique consiste à nier la possibilité d'affirmer une quelconque vérité scientifique. Mais cette position est intenable puisque si elle est vraie, elle est contradictoire (il est vrai qu'il n'y a pas de vérité) ; et si, parce qu'on veut éviter la contradiction, elle est fausse, alors elle est frauduleuse puisqu'elle est énoncée comme une vérité alors même qu'on sait que l'affirmation est fausse.
Le psychologue qui croit en la possibilité d'un savoir scientifique en psychologie est donc moralement tenu d'examiner la cohérence des pratiques et des discours qui procèdent de sa discipline. Cela vaut en particulier pour le mesurage.
4.2. Confusions et mystères
Nous prendrons pour exemple l'article de Rioux et Mokounkolo (2004), qui s'intitule "Attachement au quartier et adolescence. Étude comparative dans deux banlieues à forte diversité culturelle". On aura compris que le complément d'objet direct du verbe mesurer est ici "l'attachement au quartier des adolescents". La question de départ consiste donc à savoir si le mesurage de l'attachement au quartier d'une personne quelconque procède d'une démarche rationnelle.
Avant de répondre, assurons-nous de la réalité de l'usage en collectant quelques occurrences du verbe "mesurer" dans l'article. Nous trouvons le matériau suivant :
"En effet, mesuré à travers ses dimensions sociale et physique, l'attachement au quartier est plus intense que celui lié au logement et à la ville, la composante sociale étant la plus marquée" (p. 612).
Ainsi, l'attachement au quartier se mesure. Laissons de côté ce qu'il faut entendre par "à travers ses dimensions sociale et physique". Il s'agit bien d'une grandeur, puisqu'il peut être dit que l'attachement au quartier possède une intensité , et que cette intensité peut être comparée à l'intensité de l'attachement au logement et à l'intensité de l'attachement à la ville.
Nous aurons donc à examiner comment on fait pour mesurer l'intensité de l'attachement au quartier de quelqu'un. On trouve une autre occurrence du verbe mesurer un peu plus loin dans le texte :
"Cette échelle est composée de six items, dont deux mesurent le processus d'attachement au quartier, et quatre ses conséquences" (p. 613).
Cette phrase est riche de renseignements. Dans l'introduction, nous avons explicité que le verbe mesurer appelle un complément d'objet direct (COD) et que ce COD dénote par définition une grandeur. Mais nous n'avions pas jugé utile de préciser que le sujet du verbe mesurer est nécessairement un être humain. Ici, le verbe mesurer a deux sujets, "deux items", et "quatre items". Cette utilisation du verbe mesurer est incohérente. Le mesurage est une opération qui est effectuée par un être humain, c'est-à-dire par quelqu'un qui a une intention particulière bien qu'elle puisse être implicite, et avec un instrument ou un procédé particulier.
Ainsi, les auteurs ont l'intention de mesurer quelque chose avec des items de questionnaire. Mais, pourra-t-on se demander, en quoi un item de questionnaire peut-il s'apparenter à un procédé ou encore à une opération ? Cette formulation prête aux items la faculté de mesurer quelque chose. Ce qui constitue un authentique mystère, parce qu'un item est un ensemble de symboles couchés sur une feuille de papier ou sur un écran d'ordinateur -- une consigne, une description, et une échelle d'appréciation. Aucun principe actif dans une suite de symboles. Les auteurs escamotent la question du principe opératoire sur lequel pourrait reposer le mesurage de l'attachement au quartier -- affirmer cela serait abusif si la question était traitée ailleurs dans l'article, mais il se trouve qu'elle n'est pas abordée. Le principe du mesurage est contenu dans la capacité de la personne (à qui on demande d'apprécier les descriptions figurant dans les items du test) à produire une réponse. Mais cette capacité est une capacité linguistique. On se demande alors en quoi le fait de savoir lire et parler, et notamment de soi, permet de déterminer l'intensité de l'attachement au quartier du locuteur. Les auteurs sont muets à ce sujet.
Remettons-nous la phrase en question sous les yeux : "Cette échelle est composée de six items, dont deux mesurent le processus d'attachement au quartier, et quatre ses conséquences" (p. 613).
Dans la même phrase, le verbe mesurer accepte deux COD. Le premier COD est "le processus d'attachement au quartier". Ici, force est de constater que l'utilisation du verbe mesurer est sémantiquement impropre, puisqu'un processus n'est pas une grandeur. D'une manière générale, un processus est un ensemble de transformations qui s'opèrent sur des objets, et la notion de processus d'attachement au quartier est indéterminée puisqu'on ne sait pas quels objets sont transformés ni par quelles opérations. Il est cependant possible d'interpréter la proposition si on remplace le terme "processus" par le terme "intensité", sachant que l'intensité actuelle de l'attachement au quartier peut résulter d'un processus.
On aurait alors les phrases :
Cette échelle est composée de six items. Avec deux d'entre eux, nous obtenons les réponses de la personne interrogée, et nous déterminons, par un certain procédé, l'intensité de son attachement au quartier (comprise comme le résultat d'un processus psychologique mal connu).
Quels sont ces deux items qui permettent de mesurer l'attachement au quartier et non pas les conséquences de l'attachement au quartier ? Ici, nous sommes perdus. Les items en question (sauf la consigne qui n'a pas besoin d'être explicitée) sont listés ci-dessous.
- Pour y vivre, c'est le quartier idéal (1 : tout à fait en désaccord, 2, 3, 4, 5 : tout à fait d'accord).
- Ce quartier fait partie de moi-même (1 : tout à fait en désaccord, 2, 3, 4, 5 : tout à fait d'accord).
- Je suis très attaché(e) à certains endroits de ce quartier (1 : tout à fait en désaccord, 2, 3, 4, 5 : tout à fait d'accord).
- Il me serait très difficile de quitter définitivement ce quartier (1 : tout à fait en désaccord, 2, 3, 4, 5 : tout à fait d'accord).
- Je pourrais facilement quitter ce quartier (1 : tout à fait en désaccord, 2, 3, 4, 5 : tout à fait d'accord).
- Je n'aimerais pas à avoir à quitter ce quartier pour un autre (1 : tout à fait en désaccord, 2, 3, 4, 5 : tout à fait d'accord).
Ce qui suit n'est pas très important puisque nous avons compris que nous ne saurons pas comment il est possible de mesurer scientifiquement l'attachement au quartier. Le second COD désigne "les conséquences" du "processus d'attachement au quartier". En logique, une conséquence se déduit d'une prémisse. Peut-on identifier deux items (a, b) parmi les six proposés tels que la description contenue dans l'item a soit la conséquence de la description contenue dans l'item b ?
L'affirmation 1 n'implique aucune des affirmations 2 à 6, parce qu'on peut toujours trouver qu'il est possible d'avoir "1 = vrai" et "n'importe quelle autre affirmation = faux". Même situation pour la 2.
La 3 implique la 2 : si on est très attaché à certains endroits de son quartier, par définition, ce quartier "fait partie" de soi-même. Nous sommes néanmoins mal à l'aise avec l'argument "par définition" tant les notions sont floues. Si le quartier ne fait pas partie de moi-même, comment pourrais-je y être très attaché ? La négation de la 2 implique la négation de la 3. Donc la 3 implique la 2. ("A → B" est équivalent à "non B → non A")
La 4 implique la négation de la 5. La 5 implique la négation de la 4 et aussi la négation de la 6.
La 6 n'implique ni la 1, ni la 2 ni la 3 : en effet, dans ce dernier cas, qui paraît ambigu, il est possible de ne pas aimer à avoir à quitter le quartier pour un autre (affirmation de la 6) tout en n'étant pas très attaché à certains de ses endroits (négation de la 3), par exemple pour des raisons d'emplacement géographique qui font qu'on préfère y rester tout en étant attaché à aucun de ses endroits. Par contre, la 6 implique la 4 et la négation de la 5.
Récapitulons ces relations :
- 3 → 2,
- 4 → ˜5,
- 5 → ˜4 & ˜6,
- 6 → 4 & ˜5.
(On aura compris que la notation ˜ dénote la négation.) Il s'avère que cette analyse n'est pas cohérente avec celle des auteurs et que leur analyse demeure pour nous une obscurité. Les analyses qui précèdent ne permettent toujours pas de savoir comment l'intensité de l'attachement du quartier est déterminée en fonction des appréciations produites par la personne testée.
4.3. Le type à la place de la personne
Examinons à présent comment l'idée de grandeur est utilisée. On trouve d'autres propositions qui attestent que l'attachement au quartier s'appréhende comme une intensité :
- "Nous postulons donc que l'attachement au quartier sera plus intense en début qu'en fin d'adolescence" (p. 613).
- "[...] les femmes s'attacheraient davantage à leur quartier que les hommes" (p. 613).
- "[...] un attachement au quartier plus intense chez les jeunes filles que chez les jeunes hommes (p. 613).
L'attachement au quartier est conçu comme une grandeur mesurée de manière ordinale, c'est-à-dire que les auteurs s'intéressent à des comparaisons (plus que, moins que). D'un point de vue syntaxique, les propositions pertinentes ont la forme suivante :
L'intensité de l'attachement au quartier de X est plus grande ou plus petite que l'intensité de l'attachement au quartier de Y.
La question est alors de savoir ce que recouvrent les variables X et Y. "Les jeunes en début ou en fin d'adolescence" ne désignent personne en particulier, mais peut-être cette appellation désigne-t-elle quiconque de manière générale.
Précisons le sens de ces derniers termes à l'aide d'un exemple. Considérons l'ensemble {a, b, c, d, e}. L'élément e est un élément particulier en ce sens qu'il n'est pas a ni b par exemple. L'élément e est un élément quelconque en ce sens que j'aurais pu considérer n'importe quel autre élément de cet ensemble. Dans cette seconde perspective, je ne m'intéresse pas à ce qui fait de e un objet particulier, il me suffit de savoir qu'il appartient à l'ensemble. L'ensemble fonctionne alors comme une classe d'équivalence, ou encore une classe de référence, c'est-à-dire que ses éléments sont équivalents du point de vue du critère qui permet de les inclure dans l'ensemble.
Relisons donc la première proposition. L'attachement au quartier ne réfère à personne en particulier. Mais nous savons déjà que l'attachement ne réfère pas non plus à un adolescent quelconque, puisqu'il n'est pas question de nier les singularités des personnes de la classe "adolescents", notamment du point de vue de la manière dont les adolescents particuliers sont attachés à leur quartier. L'attachement au quartier qui intéresse les chercheurs est l'attachement au quartier de deux abstractions, ou encore de deux types : le jeune en début d'adolescence, le jeune en fin d'adolescence. Ces entités ont la fonction de résumer de manière idéalisée des réalités disparates (cf. Desrosières, 2000).
Dans la seconde proposition, l'attachement réfère aux femmes et aux hommes. La locution "Les femmes" ne désigne ni un élément particulier ni un élément quelconque, mais un ensemble de personnes ayant la propriété d'être femme. De même pour "les hommes". Il est difficile de donner un sens à l'attachement au quartier d'un ensemble ou encore d'une catégorie . Si on s'intéresse à l'attachement au quartier d'un groupe de personnes, ce sera pour se demander s'il existe ou non des différences entre ces personnes. S'il n'en existe pas, alors les personnes du groupe ne seront plus particulières mais quelconques du point de vue de l'attachement au quartier -- c'est-à-dire qu'elles seront devenues interchangeables non seulement du point de vue du critère qui fait qu'elles appartiennent au groupe, mais encore du point de vue d'un autre critère logiquement indépendant du premier (cf. la distinction entre VI et VD).
Ici, l'attachement au quartier est une grandeur qui caractérise un ensemble, indépendamment du fait que les éléments qui composent cet ensemble soient interchangeables du point de vue de la grandeur. Nous comprenons la seconde proposition en remplaçant "les femmes" par "la femme typique" et "les hommes" par "l'homme typique". Mais alors la question qui se pose est de savoir qui sont ces types. La femme typique et l'homme typique n'existent pas dans la nature. Ce sont des constructions de la pensée. Nous venons de découvrir que les auteurs s'intéressent à l'attachement au quartier de personnes typiques et non pas de personnes réelles. Les chercheurs s'intéressent ici à la psychologie de types, par opposition à la psychologie des personnes réelles. Si les chercheurs étaient des sociologues, comme les sociologues définissent leur objet comme quelque chose qui transcende les personnes d'une société, la question du statut ontologique du type -- entité qui existe indépendamment de nous ? -- se poserait d'une autre manière. Il est probable cependant que la spécificité du social par rapport au psychologique ne se réduise pas à la notion statistique de typicité.
La troisième proposition s'interprète de la même manière : les auteurs s'intéressent à la jeune fille et au jeune homme typiques. Le problème qui se pose maintenant est de savoir comment on fait pour mesurer l'attachement au quartier de ces types.
4.4. Mesurer l'attachement au quartier d'un type
Pour mesurer l'attachement au quartier d'un type, on va d'abord construire ce type de manière à ce qu'il puisse être appréhendé empiriquement. Autrement dit, on veut matérialiser ce type. On peut identifier quatre étapes :
- On doit d'abord résoudre le problème du mesurage de l'attachement au quartier de quiconque à un moment quelconque, ce qui permettra de donner au résultat du mesurage le statut d'un événement empirique.
- Le procédé même du mesurage définit un espace d'échantillonnage (sampling space), c'est-à-dire l'ensemble de tous les événements élémentaires qui peuvent en principe se produire lorsqu'on fait une expérience de mesurage, c'est-à-dire lorsqu'on mesure l'attachement au quartier de quiconque à un moment quelconque (i.e., un point dans la population).
- On procède alors à l'échantillonnage, c'est-à-dire qu'on effectue un certain nombre de mesurages auprès d'un échantillon de points (i.e., de couples (personne, moment)).
- On choisit ensuite un indice de centralité (i.e., une statistique, comme le mode ou la moyenne) pour calculer la valeur prise par la statistique du type.
Avant d'entrer dans les détails, insistons sur le point suivant : connaître la valeur prise par la statistique associée à l'échantillon ne permet pas de régler complètement le problème de la matérialisation du type. Car le type correspond à une distribution de probabilité qui est par construction inconnue et inconnaissable. La statistique d'échantillon ne nous donnera donc qu'une image partielle du type. Le principe même du type est que cette image varie : il y a autant d'images que d'échantillons possibles, et on sait que ces échantillons sont différents les uns des autres, puisqu'il existe des différences individuelles du point de vue de ce qui est mesuré. Cette variabilité est ce qu'on appelle en statistique l'erreur d'échantillonnage, ou encore, au pluriel, les fluctuations d'échantillonnage (voir Population et échantillons).
Le problème de recherche est posé de telle manière que le type restera toujours inconnu d'un point de vue empirique, et qu'on parlera de lui en se fondant sur quelques-unes de ses images. En général, le chercheur en psychologie se contente d'une seule image. Du point de vue philosophique, le chercheur en psychologie s'intéresse ici à une fiction qui n'a pas la vocation de correspondre à quiconque à un instant quelconque. Son objet d'étude est un pur concept (i.e., il ne correspond pas à quoi que ce soit de réel, mais, en tant que concept, il constitue une réalité sociale, parfois très utile pour les stratèges de la vente et de la communication -- cf. la description des goûts de la mère de famille moyenne en matière d'alimentation).
Revenons donc au premier sous-problème à résoudre : mesurer l'attachement au quartier de quiconque à un moment quelconque. La solution est simple. On se donne les six questions d'attachement au quartier, ce qui permet de décrire quiconque répond aux questions à un moment quelconque. Ainsi, on règle le problème insoluble suivant : comment rendre le vécu observable ? Mais ne soyons pas naïfs, ce qui est observé n'est pas le vécu, mais un ensemble de réponses qui dépend pour une part du vécu de la personne et pour une part des questions qu'on lui pose et du format des réponses qu'on lui impose.
Prévenons un malentendu : le problème n'est pas que le domaine des observables soit contingent, c'est qu'on l'identifie avec le vécu. Si on veut étudier la psychologie des gens de manière scientifique, il faut bien s'appuyer sur des descriptions objectives (cf. Mesurer ou décrire ?). Mais si on veut étudier de manière objective le vécu de Paul par rapport à son quartier, alors on a un problème insurmontable, c'est qu'on ne peut pas se glisser dans son vécu. Le problème en psychologie est de cultiver la naïveté qui consiste à croire qu'on peut faire une science du subjectif grâce à ce qu'on appelle des mesures psychologiques. Aucun mesurage n'est capable d'atteindre le subjectif, pour des raisons non pas technologiques, mais logiques. Il n'est logiquement pas possible d'affirmer que A est égal à non A. Or le mesurage, en tant que forme particulière d'observation, est un processus d'objectivation. Le raisonnement qui précède a une conséquence étonnante : c'est qu'un questionnaire donne accès à un monde de réponses aux items du questionnaire. La technique du questionnaire permet éventuellement de développer une science des réponses à des questions. Et les réponses des gens aux items du questionnaire ne correspondent pas à l'intensité de l'attachement au quartier parce que cette notion dénote un vécu. La négation de ces limites logiques constitue une erreur scientifique. Cette erreur peut se transformer en attitude frauduleuse si on persiste dans l'erreur en toute connaissance de cause.
On dispose d'une technique pour recueillir des observations lorsqu'on interroge quiconque à un moment quelconque (négligeons la nécessité que cette personne soit disposée à ce moment pour bien vouloir répondre à nos questions). Partant, nous avons défini notre espace d'échantillonnage, à ne pas confondre avec l'échantillon : l'espace d'échantillonnage est l'ensemble de toutes les réponses possibles à notre questionnaire. Une réponse est la donnée des six réponses à notre questionnaire, c'est un 6-uplet (plus généralement, on parlera d'un vecteur ou d'un m-uplet, m indiquant le nombre de données contenues dans le vecteur). Par exemple, le 6-uplet (1, 2, 1, 3, 4, 1) est une réponse possible au questionnaire.
Le problème qui surgit immédiatement est qu'on ne sait pas traduire ce 6-uplet en degré d'intensité d'attachement au quartier. Ceci devrait nous faire douter du bien-fondé du projet de mesurage de l'intensité de l'attachement au quartier. Non seulement, le vécu n'est pas pénétrable, mais encore les observables qui résultent de la technique du questionnaire n'ont pas le caractère logique d'une grandeur. Face à ce problème, les chercheurs adoptent une solution symbolique (et non pas instrumentale ), qui prend ici la forme suivante :
- recoder les réponses de la question 5 à l'envers : 1 devient 5, 2 devient 4, etc. jusqu'à 5 devient 1;
- additionner les chiffres du 6-uplet.
On obtient ainsi un score d'attachement au quartier, et donc un nouvel espace d'échantillonnage qui est l'ensemble des nombres {6, 7, ..., 30} (cf. Score psychométrique).
Note. Rioux et Mokounkolo utilisent ce qu'on appelle des "scores factoriels", qui sont des nombres issus d'opérations arithmétiques complexes, dont la spécification repose sur les données d'un échantillon. Mais ces calculs ne modifient pas le caractère logiquement frauduleux du mesurage parce qu'ils reposent sur l'additivité des nombres qui codent les réponses aux questions des items, quand bien même personne ne sait ce que signifie l'addition des degrés de réponse constituant les échelles de réponse (pas du tout d'accord + tout à fait d'accord = ?).
Grâce à ce procédé symbolique, il est possible de sonder le type qui nous intéresse, par exemple "les jeunes filles", en interrogeant par exemple 200 jeunes filles satisfaisant ce qu'on appelle des critères d'inclusion (par exemple, avoir entre 12 et 25 ans). Concrètement parlant, un type comme "les jeunes filles" est un type trop vague, parce qu'il faut exclure les jeunes filles chinoises par exemple.
Ainsi équipé, le chercheur peut comparer le mode d'un échantillon de manifestations du type "les jeunes filles" au mode d'un échantillon de manifestations du type "les jeunes garçons". Ces deux modes servent de mesures de l'intensité de l'attachement au quartier des deux types, sachant que l'erreur d'échantillonnage empêche d'être tout à fait sûr que le résultat de la comparaison, par exemple, le fait que le premier mode soit supérieur au second, sera reproductible si on utilise deux autres échantillons.
4.5. Mesurage psychologique et irrationnalité
Notre point de départ consistait à exiger l'absence d'incohérence logique dans la démarche scientifique, en particulier dans la démarche du mesurage d'une grandeur psychologique. L'exemple de l'étude de Rioux et Mokoukolo (2004) sur l'attachement au quartier des adolescents nous a permis d'identifier trois types d'incohérence logique et la promulgation de leur dénégation via une doctrine méthodologique devenue internationalement dominante depuis la fin de la moitié du XXe siècle (e.g., Danziger, 1990 ; Lamiell, 2003) :
- la dénégation de l'impossibilité logique de mesurer une grandeur subjective,
- la dénégation du caractère qualitatif et non ordinal de l'espace d'échantillonnage, utilisé à pleine puissance pour décrire les personnes et ensuite remplacé par un autre espace d'échantillonnage composé de scores,
- la dénégation des différences individuelles qui existent entre les personnes regroupées sous une catégorie et leur remplacement par la description, nécessairement partielle, du type qui les subsume.
Cette triple dénégation n'est pas gratuite. Elle permet de maintenir, en dépit des difficultés soulevées, le projet de mesurer des grandeurs psychologiques. Une telle attitude pourrait être décrite dans une perspective psychanalytique comme la dénégation du principe de réalité. Curieusement, un argument souvent opposé à la critique que nous avons développée est qu'il n'est pas réaliste de renoncer à la méthodologie mise en œuvre, de manière exemplaire, par Rioux et Mokounkolo (2004). Mais ce réalisme-là n'a pas grand-chose à voir avec l'éthique de la connaissance scientifique, qui refuse en particulier la toute puissance d'un utilitarisme dont les fondements ne sont pas toujours explicites (cf. Canguilhem, 1958).
Il est clairement réaliste de développer une science des réponses aux questionnaires psychologiques, si tant est que les questionnaires psychologiques constituent un mode d'objectivation privilégié en psychologie. Et il est parfaitement réaliste de considérer qu'une science empirique est par définition une science des phénomènes empiriques auxquels elle sait accéder (qu'elle sait décrire).
4.6. Exercices corrigés
Critiquer les affirmations suivantes du point de vue méthodologique. On pourra s'aider en utilisant les questions suivantes:
- Est-il question de personnes quelconques (si oui, dans quel ensemble de référence sont-elles regroupées), particulières (si oui, de qui s'agit-il), ou typiques (si oui, vérifier qu'elles ne sont ni quelconques, ni particulières) ?
- L'ensemble des valeurs des variables (grandeurs mesurées, ou caractéristiques descriptives) peut-il être spécifié (si oui, quel est-il) ?
Exercice 1. En moyenne, les fumeurs meurent plus jeunes que les non fumeurs.
La durée de vie peut se mesurer en années. Les fumeurs et les non fumeurs renvoient à des personnes typiques (il ne s'agit pas de comparer les durées de vie d'un fumeur et d'un non fumeur quelconques, ni d'un fumeur et d'un non fumeur particuliers -- Jean qui était fumeur peut très bien avoir vécu plus longtemps que Paul qui était non fumeur).
Exercice 2. On considère un questionnaire de deux items à 5 modalités de réponse (1, 2, ..., 5). Les gens étudiés dans une certaine condition C choisissent systématiquement les degrés 4 ou 5.
On décrit des personnes qui se trouvent dans la condition C. Ces personnes sont décrites dans l'ensemble {11, 12, 13, ..., 55}, qui comprend 5 × 5 = 25 couples de réponses possibles. Le phénomène décrit est remarquable, puisque les réponses d'une personne quelconque (ou, dit autrement, de toute personne sde trouvant dans la condition C) appartiennent au sous-ensemble {44, 45, 54, 55}, soit 4/25e de l'espace d'échantillonnage.
Exercice 3. Un chercheur utilise un questionnaire d'anxiété composé de 10 items cotés sur une échelle de quatre degrés d'accord. Le score d'anxiété de Paul est en moyenne plus élevé lorsque Paul est de mauvaise humeur.
Le chercheur mesure l'anxiété de Paul avec un questionnaire. Le score résulte d'un traitement symbolique des réponses de Paul au questionnaire. Il n'est pas exclu que ce traitement soulève des difficultés logiques puisqu'on ne sait pas en quoi un vecteur de réponses, c'est-à-dire la donnée des 10 réponses, pourrait représenter une quantité ou un degré. On ignore la taille des échantillons d'observations ainsi que la procédure qui permet de déterminer la qualité de l'humeur.
Exercice 4. La fréquence de la réponse "oui" à la question "Je me sens anxieux : oui ou non" est plus élevée lorsqu'on est de mauvaise humeur.
Un chercheur observe la réponse de quiconque à la question "Je me sens anxieux : oui ou non", selon l'humeur considérée comme "mauvaise" ou "non mauvaise". L'affirmation est évasive pour deux raisons :
- la taille de l'échantillon des réponses observées n'est pas précisée,
- la procédure de classification de l'humeur n'est pas précisée.
Exercice 5. Un chercheur mesure l'agressivité de joueurs de jeux video qu'il a affecté au hasard à deux conditions expérimentales. Les joueurs qui jouent à des jeux video violents sont plus agressifs que les joueurs qui jouent à des jeux video non violents.
Il s'agit de joueurs typiques -- des joueurs expérimentaux --, dont on décrit l'agressivité de façon évasive. On ne sait pas par quel procédé l'agressivité est mesurée. Si l'espace d'échantillonnage est constitué de plusieurs items (par exemple, proférer des injures, frapper le clavier), une observation est un vecteur. D'où le problème de savoir comment représenter des vecteurs sur une échelle.
5. Opérationnaliser une grandeur psychologique

Objectifs Montrer comment un score peut être interprété comme la mesure d'un construit et en quoi cette interprétation ne peut pas être une explication scientifique.
Prérequis.
Résumé. Selon l'article intitulé "Relations entre Statistique et Psychométrie" (§ 3, cours de L1), la psychométrie s'occupe de la conceptualisation des scores obtenus à l'aide de tests ou questionnaires psychométriques. Pourquoi conceptualiser les scores psychométriques ? Si on ne connaissait pas de possibilité pour interpréter les scores comme mesures d'une grandeur hypothétique, il serait impossible d'utiliser les scores comme des mesures de quoi que ce soit.
5.1. Les scores psychométriques sont des artefacts
Dans un ouvrage critique, Kurt Danziger (1990) écrit ceci :
But in truth scientific psychology does not deal in natural objects. It deals in test scores, rating scales, response distributions, serial lists, and innumerable other items that the investigator does not find but constructs with great care. Whatever guesses are made about the natural world are totally constrained by this world of artifacts (p. 2).
Ce que nous traduirons comme cela :
Mais, en vérité, la psychologie scientifique n'a pas affaire à des objets naturels. Elle a affaire à des scores psychométriques, à des échelles de réponse, à des distributions de réponses, à des listes ordonnées, et à d'innombrables choses de ce genre, que les chercheurs ne trouvent pas, mais élaborent soigneusement. Quelles que soient les conjectures qui sont faites à propos du monde naturel, elles sont totalement déterminées par cet univers d'artefacts.
Quand on y regarde de près, c'est évident : les scores psychométriques ne sont pas des données, mais des artefacts. Ce sont des événements constitués dans un univers artificiel, c'est-à-dire un univers qui est fabriqué (par les psychologues).
Par conséquent, le psychologue est tenu de connaître les procédés de fabrication des scores psychométriques, car il est supposé compétent pour répondre de leur signification. L'article intitulé "Score psychométrique" (cours de L1) décrit en détail comment les scores de tests sont fabriqués.
Les scores de tests ont une double signification. Lorsqu'on regarde comment ils sont fabriqués, ils correspondent à des classes de réponses. Lorsqu'on regarde ce qu'ils sont supposés représenter, ils correspondent à des différences relatives à une grandeur métaphorique, un "construit" (e.g., l'anxiété-trait).
Leur signification opératoire pose un problème de cohérence. Leur signification métaphorique pose également un problème de cohérence. Ces problèmes sont généralement ignorés (méconnus ou négligés) par leurs utilisateurs. Tout se passe comme si les scores psychométriques étaient sinon des mesures, du moins des données quantitatives prêtes à être introduites dans des analyses statistiques. Les problèmes de cohérence opératoire des scores psychométriques sont développés dans l'article La confusion nominale induite par les scores psychométriques.
Le présent article se focalise sur les problèmes de cohérence métaphorique des scores psychométriques et introduit les solutions interprétatives de la théorie classique des tests et de la modélisation de la réponse à l'item. Une solution interprétative est une solution fondée sur une interprétation, c'est-à-dire sur l'invention d'une possibilité de se figurer comment il est possible d'observer ce qu'on observe. Elle s'oppose à une explication scientifique, qui non seulement explicite comment il est possible d'observer ce qu'on observe, mais encore comment il est nécessaire qu'on observe ce qu'on observe et pas autre chose. (Pour approfondir, voir Vautier, Veldhuis, Lacot, & Matton, 2012).
5.2. Comment passer du discret au continu ?
Considérons un questionnaire d'anxiété-trait dont l'échelle de scores varie de 0 à 40 points. Les scores sont obtenus par l'addition des 10 scores élémentaires obtenus aux 10 questions du test d'anxiété, chaque score élémentaire variant dans la suite (0, 1, 2, 3, 4). On remarque immédiatement qu'il est impossible d'observer le score 2,3 points par exemple, du fait de la conception même du score psychométrique. Donc, d'un point de vue empirique, la grandeur varie dans la suite (0, 1, ..., 40), c'est-à-dire qu'il y a 40 sauts (le saut de 0 à 1, le saut de 1 à 2, etc.).
Or, d'un point de vue métaphorique, l'anxiété-trait n'est pas une grandeur discrète, mais continue. Un continuum est une grandeur telle qu'on passe d'un niveau à un autre sans saut. L'intuition psychologique selon laquelle l'anxiété-trait serait comme un attribut quantitatif ne spécifie ni sauts ni paliers. Par défaut, cet attribut quantitatif est donc un continuum. D'où un problème logique : comment peut-on mesurer, c'est-à-dire mettre en correspondance, une grandeur continue avec 41 paliers ?
La théorie classique des tests définit le continuum [0, 40], dans lequel variera le "score vrai", tandis que la modélisation de la réponse à l'item définit un continuum non borné (i.e., l'ensemble des nombres réels), dans lequel variera le "trait latent". Ces deux vocables constituent des constructions quantitatives mobilisées pour opérationnaliser l'intuition d'une grandeur psychologique continue.
5.3. La solution de la théorie classique des tests
1) Prenez quelqu'un, demandez-lui de répondre au questionnaire, calculez son score et enregistrez-le.
2) Effacez-lui la mémoire.
3) Assurez-vous que les conditions expérimentales n'ont pas changé.
4) Demandez-lui de répondre au questionnaire, calculez son score et enregistrez-le.
5) Recommencez les opérations 2, 3 et 4 toute votre vie, et si possible ne mourez jamais car la série de vos scores doit être infinie.
6) Lorsque vous avez fini de recueillir vos scores, calculez la moyenne : vous venez de découvrir le score vrai.
Ce score, qu'on appelle aussi une espérance mathématique, est une impossibilité empirique, une pure vue de l'esprit. Cela est obligatoire, puisque l'anxiété-trait est aussi une pure vue de l'esprit. Ainsi, une vue de l'esprit de caractère mathématique opérationnalise une vue de l'esprit de caractère métaphorique. Une simulation illustrative est disponible dans l'article Variable aléatoire (cours de L1).
À partir de là, toute l'histoire consiste à trouver comment on peut estimer la précision avec laquelle on estime le score vrai. Notons au passage qu'on ne mesure plus, on estime. C'est-à-dire qu'on se livre à de savants développements de l'opérationnalisation initiale, développements qu'on pourrait appeler théorie de la fidélité.
Pour l'instant, ce qui nous intéresse, c'est comprendre comment les scores peuvent être interprétés, à rebours, comme ce qui a résulté d'un processus de mesure. Pour donner une signification opératoire au score vrai, on le déduit d'une série de scores qu'on a obtenus par une expérience de pensée. Maintenant, on se passe de tout score observé et on considère qu'il y a le score vrai : il existe indépendamment de la série des mesures. Ce faisant, on fait appel à un postulat métaphysique, ce qui permet de dépasser le paradoxe du caractère non opératoire d'une chose définie par le biais d'une expérience de pensée. Maintenant, le score vrai est premier, il ne résulte plus de la moyenne des mesures.
Ensuite, il y a le mesurage, qui engendre des biais. Ces biais s'ajoutent donc au score vrai, ce qui donne le score observé. Notons que ce processus de mesurage est tout à fait magique. Et l'identification de la grandeur métaphorique avec le continuum est une pure convention. Écrivons cela de manière mathématique. Notons τ (tau) le score vrai, ε (epsilon) les biais et y le score observé. On a la définition suivante :
y = τ + ε.
Il faut maintenant montrer comment le score vrai peut varier sur le continuum [0, 40]. Pour cela, il suffit de faire un pas de plus dans l'écriture de la définition de τ . Ce pas va nous permettre de montrer comment est mobilisée une deuxième pure vue de l'esprit, corollaire de la première : la probabilité d'un événement (un score, étant donné le score vrai). On va considérer qu'il existe 41 probabilités :
1) la probabilité, étant donné
τ, d'obtenir le score 0, qui sera notée
p0,
2)la probabilité, étant donné τ, d'obtenir le score 1, qui sera notée p1,
etc. jusqu'à...
41) la probabilité, étant donné τ, d'obtenir le score 40, qui sera notée p40.
Ces probabilités ne sont rien d'autre que la fréquence de chaque score, lorsque cette fréquence est calculée avec l'infinité des mesures acquises par l'expérience de pensée initiale. On considère aussi comme certain le fait qu'on obtiendra un score lorsqu'on administrera le questionnaire (on néglige la situation du répondant qui refuse de répondre). Ainsi, la somme des probabilités de chaque score vaut 1 :
p0 + p1 + ... + p40 = 1.
Avec ces probabilités, on a une autre définition du score vrai :
τ = 0× p0 + 1× p1 + ... + 40× p40.
Pour montrer que τ peut varier dans [0, 40], il faut montrer qu'il ne peut pas varier à l'extérieur de [0, 40] et qu'il peut prendre n'importe quelle valeur dans [0, 40]. Pour une démonstration que τ appartient à [0, 40], voir l'article Encadrement de l'espérance d'une variable aléatoire numérique discrète bornée. Nous allons nous contenter ici d'une approche intuitive.
Existe-t-il un minimum et un maximum de τ ? On a un jeu de scores possibles et un jeu de probabilités dont on fait ce qu'on veut du moment que leur somme reste égale à 1. Pour minimiser τ, il faut maximiser la probabilité d'avoir le score minimum, c'est-à-dire fixer p 0 à 1, ce qui implique que les probabilités restantes ont pour valeur 0, ce qui implique que min(τ) = 0×1 = 0. Un raisonnement analogue conduit à max(τ) = 40×1 = 40.
Nous déduisons que τ varie dans l'intervalle [0, 40]. Rien n'interdit que τ prenne des valeurs réelles. Autrement dit, le recours aux 41 probabilités permet de concevoir comment τ varie dans un continuum borné.
Il reste à fonder ces probabilités comme des êtres qui possèdent une signification scientifique. À notre connaissance, personne n'a réussi une telle prouesse; en effet, il faudrait pouvoir mettre en œuvre le programme expérimental esquissé plus haut, ou être capable de voyager dans le temps. Ainsi, la théorie classique des tests est cohérente, elle mesure des grandeurs métaphoriques avec des scores vrais qu'on ne connaîtra jamais, puisqu'il faudrait connaître les probabilités de chaque score observé et qu'on ne connaîtra jamais ces probabilités, puisqu'il faudrait, entre autres choses, être immortel. Mais on a tout de même une théorie de ce qui est mesuré... Nous verrons que cette théorie est infalsifiable, et n'est donc pas une théorie scientifique d'un point de vue poppérien; elle reste une théorie interprétative qui peut très bien convenir si on lui demande seulement de fournir une interprétation du score comme mesure d'une grandeur intuitive.
5.4. La solution de la modélisation de la réponse à l'item
La modélisation de la réponse à l'item prend le problème de la relation entre le score discret et le continuum au niveau non pas du score composite, mais des scores élémentaires. Ici, nous nous bornerons à examiner le cas des items dichotomiques, c'est-à-dire des items variant dans (0, 1).
L'idée de base est très simple, analogue à l'idée du score vrai, quoique un peu plus sophistiquée. On considère un continuum et on suppose qu'une personne qui répond à un item possède un score sur ce continuum, qu'on note 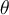 (theta). Ici, point d'expérience de pensée, le continuum existe et tout individu y occupe une position. Étant donné cette position, on considère qu'il existe une probabilité
p
1
(theta). Ici, point d'expérience de pensée, le continuum existe et tout individu y occupe une position. Étant donné cette position, on considère qu'il existe une probabilité
p
1
5.5. L'infalsifiabilité des opérationnalisations psychométriques
Une proposition falsifiable est une proposition qui peut s'avérer fausse. Une proposition qui peut s'avérer fausse est une proposition qui permet la possibilité d'affirmer qu'une proposition contradictoire soit vraie. Dans toute la théorie qui précède, peut-on trouver une proposition qui pourrait s'avérer fausse ? Il semble que non.
Considérons tout d'abord la proposition
y = τ + ε.
Soit y un score observé. On affirme qu'il existe un nombre τ dans [0, 40] et un nombre réel ε tels que leur somme vaut y. Ceci ne peut pas être faux. Cette proposition est donc infalsifiable.
Considérons maintenant la proposition
p0
=
p1
= ... =
p40
= 1/41
(et alors τ = 1/41(0+1+...+40) = 20). Peut-on falsifier cette proposition ? Pour un sujet qui se souvient et une condition expérimentale donnés, on peut observer un score compatible avec ces probabilités puisque la théorie ne limite pas le domaine de ε. Pour qu'une proposition de ce genre soit falsifiable il faut qu'elle stipule qu'au moins une des probabilités est nulle, auquel cas elle interdit que le score dont la probabilité est nulle puisse être observé. La théorie classique des tests ne spécifie pas ce type de cas.
Considérons maintenant la modélisation de la réponse à l'item. Par définition, tout sujet est doté d'un score θ. Tant que la théorie évite d'attribuer une probabilité nulle ou totale (égale à 1) à l'événement 1, toute proposition spécifiant les valeurs de θ et de p1 est infalsifiable.
Nous avons dit qu'un modèle de réponse à l'item stipule que la probabilité de l'événement 1 augmente avec θ. Pour tester une telle proposition, il faudrait pouvoir utiliser le trait latent comme une variable indépendante. Malheureusement, par définition, le trait latent n'est pas une variable que l'on peut manipuler expérimentalement ni même une variable observable.
C'est pourquoi nous considérons que les modèles psychométriques n'ont pas de vocation scientifique (au sens poppérien du terme), mais une vocation interprétative.
6. Approche intuitive de la statistique inférentielle
Objectifs. Introduire la notion d'inférence statistique.
Prérequis.
Résumé. L'article pose le problème fondamental auquel tente de répondre la notion d'inférence. Une présentation intuitive de ce problème est proposée et on montre qu’il existe une réponse intuitive à ce problème, une inférence statistique naïve. La démarche statistique classique n’est alors qu’une réponse formelle, systématique et mathématisée, à ce problème naturel.
1. Approche Intuitive de la statistique inférentielle
L’histoire du pouvoir télékinétique de Mr Magic … ou la preuve que vous possédez déjà intuitivement la démarche statistique !

En vacances dans un endroit très touristique, vous croisez un magicien et des badauds « Approchez mesdames et messieurs, venez voir M. Magic, l’homme qui peut contrôler les objets par le pouvoir de sa pensée ! ». Bien entendu, être de raison, vous êtes plus que sceptique. L’homme ajoute « Regardez mesdames et messieurs, M. Magic peut faire tomber la pièce de monnaie du côté que vous voulez… » Un enfant parmi les spectateurs demande alors au magicien de faire tomber la pièce sur le côté pile. « Regardez mesdames et messieurs M. Magic va faire tomber la pièce sur pile ! ». Il lance la pièce en l’air et, effectivement, la pièce tombe sur pile. « Et voilà, mesdames et messieurs, la démonstration du pouvoir télékinétique de M. Magic ! ».
À cet instant, ayant suivi l’échange et la « démonstration » du coin de l’œil, la première idée qui vous vient à l’esprit risque d’être : « bah, c’est sans intérêt, de toute façon il y avait une chance sur deux que la pièce tombe du bon côté ».
Prenons le temps d’analyser cette réaction. Le magicien a obtenu le résultat qu’il avait annoncé, donc, en droit, on pourrait se dire que son affirmation initiale a été corroborée par l’expérience. Mais voilà, vous savez pertinemment que le hasard seul est largement suffisant pour expliquer cette observation. Vous devez donc trancher entre deux explications (au moins),l’une facile à croire, l’effet du hasard, l’autre très difficile à croire,l’effet de la télékinésie. Eh bien, par ce raisonnement simple, vous venez de réaliser un véritable test de signification statistique. Vous aviez d’un côté l’hypothèse énoncée par le magicien, le pouvoir télékinétique. D’un autre côté, vous avez mobilisé l’hypothèse que le hasard pourrait expliquer le résultat observé. Cette deuxième hypothèse revient à dire qu’en réalité, l’effet télékinétique est nul, et donc on appelle cette deuxième hypothèse« hypothèse nulle ». Vous vous trouvez donc à devoir choisir, décider, entre deux hypothèses contradictoires pour expliquer l’observation empirique. L’hypothèse du magicien ou l’hypothèse nulle. A priori, vous n’êtes pas prêt à croire à l’hypothèse du magicien. À combien évaluez-vous la probabilité a priori que cette explication soit bonne ? Une chance sur mille ? Sur dix mille ? Sur un million ? Quoi qu’il en soit, en comparant une chance sur 2 pour que la pièce tombe du bon côté par hasard et les chances qu’on ait affaire à un super pouvoir, la décision est vite prise : vous choisissez de croire à l’effet du hasard. Vous acceptez l’hypothèse nulle et le test du magicien n’a pas été concluant.
En fait, c’est même tellement évident que vous vous doutez déjà que le magicien ne va pas en rester là. Le grand frère du petit garçon lui-même s’exclame « c’est un coup de chance ! Je parie que vous ne pouvez pas le refaire… »
« Eh bien, mesdames et messieurs, Monsieur Magic peut le refaire, autant de fois que vous le voulez ! ». Et, sur ce, il lance trois fois la pièce et trois fois elle tombe sur pile. Vous commencez à douter car, quatre lancers de suite qui tombent sur pile par hasard, vous savez que c’est encore possible, mais moins fréquent. Mais, néanmoins, c’est encore suffisamment possible pour que vous ne changiez pas votre opinion.
Analysons cette deuxième partie de l’histoire. Le point intéressant maintenant, c’est que même sans faire formellement le calcul, vous savez – et même l’enfant le sait aussi – que la probabilité de sortir pile au hasard 4 fois de suite (la première fois et les trois fois suivantes) est faible. Effectivement, l’analyse mathématique du problème donne pour cette probabilité une chance sur 16, soit 6% de chances environ. Mais cela reste quand même possible.
Poursuivons notre histoire, car vous avez déjà bien compris que le magicien ne s’arrêterait pas là… et effectivement, il lance encore dix fois la pièce et dix fois elle tombe sur pile. « Et voilà, mesdames et messieurs, la démonstration irréfutable du pouvoir télékinétique infaillible de Mr Magic ! ». Mais bon, on ne vous la fait pas. Vous pensez immédiatement que la pièce doit être truquée pour tomber sur pile. Pas la peine d’adopter une croyance invraisemblable comme la télékinésie.
Analysons maintenant cette troisième partie. Cette fois, vous êtes bien convaincu que le hasard n’est pour rien dans le résultat des lancers de pièce. De fait, si l’on fait le calcul, cette probabilité est nettement trop faible pour qu’on puisse adopter sans autre forme de procès l’hypothèse que le hasard puisse expliquer cette série de 14 côtés pile (moins d’une chance sur 16000 en fait). Donc, même sans calcul explicite, vous avez spontanément abandonné cette explication. Vous, tout comme l'enfant, avez « rejeté l’hypothèse nulle ».
Sans le savoir, vous avez donc entièrement réalisé la démarche d’un test statistique. La seule véritable différence tient au fait que vous avez utilisé vos intuitions de probabilité et votre intuition du degré de risque acceptable ou non, plutôt que d’utiliser des routines mathématiques reconnues et des conventions sociales en vigueur dans la communauté scientifique concernant l’acceptabilité des hypothèses. Dans les articles suivants, et en particulier dans les grandes leçons dédiées aux statistiques inférentielles, nous examinerons de plus près comment la statistique, en tant que discipline, formalise ces intuitions pour des calculs rigoureux.
En résumé:
- Pour expliquer un phénomène observé (phénomène généralement exprimé par un jeu de statistiques descriptives), on a toujours au moins deux hypothèses, l’hypothèse nulle (le hasard explique ce qu’on a observé) et l’hypothèse alternative (il existe un effet systématique derrière les résultats observés, peut-être l'hypothèse du chercheur ou un autre effet systématique inconnu comme un biais méthodologique) ;
- Si le hasard semble pouvoir expliquer facilement les résultats, on privilégie l’hypothèse du hasard, l’hypothèse nulle.
- S’il semble invraisemblable que le hasard puisse expliquer les résultats, on admet sans difficulté qu’il y a « quelque chose », autrement dit, on rejette l’hypothèse nulle (mais sans nécessairement accepter l’hypothèse du chercheur).
Ces trois points constituent les bases de la « statistique inférentielle ». C’est-à-dire une approche formelle visant à prendre exactement la même décision (accepter ou rejeter l’hypothèse que le hasard explique les résultats observés) mais en s’appuyant sur une analyse rigoureuse des situations étudiées.
En particulier, les statisticiens s'attachent à préciser des méthodes rigoureuses de calcul de la probabilité que l'hypothèse nulle soit la bonne. L'étude de quelques-unes de ces méthodes est précisément l'objet de ce cours.
7. L'hypothèse nulle
Objectifs. Définir la notion d'hypothèse nulle et son utilité dans la pratique statistique
Prérequis.
- Articles sur la variabilité de la grande leçon "Psychologie, statistique et psychométrie" du cours de L1;
- Approche intuitive de la statistique inférentielle
Résumé.
L'hypothèse nulle, généralement notée  , traduit ce qu'on pourrait prédire de la réalité si celle-ci n'était gouvernée que par le hasard. L'hypothèse nulle sert de point de référence pour la démarche statistique : une fois qu'on a su la spécifier formellement dans une situation donnée, on peut calculer un modèle de ce que prédit cette hypothèse. Si les données sont suffisamment différentes de la prédiction faite sous l'hypothèse
, traduit ce qu'on pourrait prédire de la réalité si celle-ci n'était gouvernée que par le hasard. L'hypothèse nulle sert de point de référence pour la démarche statistique : une fois qu'on a su la spécifier formellement dans une situation donnée, on peut calculer un modèle de ce que prédit cette hypothèse. Si les données sont suffisamment différentes de la prédiction faite sous l'hypothèse  , on pourra considérer que quelque cause systématique a agi sur la situation. La nature exacte de cette cause n'est cependant PAS fournie par l'analyse statistique, même si le chercheur avait son hypothèse là-dessus).
, on pourra considérer que quelque cause systématique a agi sur la situation. La nature exacte de cette cause n'est cependant PAS fournie par l'analyse statistique, même si le chercheur avait son hypothèse là-dessus).
En conséquence, si dans un test on rejette l'hypothèse nulle, cela signifie qu'on rejette un modèle où le hasard suffirait à tout expliquer sans toutefois qu'on puisse être sûr que l'hypothèse du chercheur est valide. Si on ne rejette pas l'hypothèse nulle cela revient à dire que les données ne permettent pas d'appuyer une hypothèse plus compliquée qu'une simple résultat aléatoire.
7.1. Définition et exemples
1.1. Définition.
On appelle hypothèse nulle une prédiction faite sur le comportement d'une réalité donnée, prédiction ne supposant pas d'autre facteur actif qu'une simple répartition aléatoire des événements possibles.
1.2. Quelques exemples.

Supposons que je jette une pièce non truquée en l'air. Chacun sait qu'il y a une chance sur deux qu'elle retombe sur pile et une chance sur deux qu'elle retombe sur face. Une autre façon de le dire est de prévoir que si je jette la pièce en l'air 1000 fois, elle tombera environ 500 fois sur pile et environ 500 fois sur face. Cette prédiction ne fait appel à aucun autre mécanisme hypothétique que le seul « effet du hasard » (qui n'existe pas à proprement parler, le hasard étant plutôt l'absence de détermination). C'est donc un cas d'hypothèse nulle.
Prenons maintenant un dé non pipé. Il y a six faces donc l'hypothèse nulle prédit que, sur un grand nombre de tirages, chaque face sortira environ 1/6 des tirages.
L'idée est assez simple, même si l'on se doute que le calcul, lui, peut être parfois bien plus compliqué que pour un tirage à pile ou face... Mais à quoi cela sert-il ?
7.2. Utilisations de l'hypothèse nulle en statistique
2.1. Quelque chose plutôt que rien ?
Fondamentalement, le scientifique veut comprendre le monde. Le monde se donne à lui par les sens, mais les observations sont soumises à la variabilité. De sorte que comprendre le monde revient à savoir repérer et expliciter les causes à l'œuvre sous le processus de construction de la réalité observable. Mais voilà, la réalité est fluctuante et les mesures imprécises. De ce fait, quelle que soit l'observation réalisée, il existe toujours une possibilité que ce que l'on a observé ne soit que le pur fruit du hasard. Il faut donc se prémunir contre ce risque. Pour cela, une solution simple utilise la notion d'hypothèse nulle. Puisque celle-ci représente l'hypothèse que ce que l'on a observé est le pur fruit du hasard, il suffit de produire une prévision de ce qu'aurait donné le hasard puis de vérifier si les données sont suffisamment loin de cette prévision pour pouvoir conclure que quelque chose est à l'œuvre qui n'est pas le hasard.
Cette idée s'applique assez directement, par exemple, dans l'analyse du caractère truqué ou non d'une pièce. Si la pièce tombe 30 fois de suite sur pile, on imagine bien que le hasard ne prédit que très rarement la survenue d'une telle série de lancers (1 fois sur 230 séries en fait, soit quelque chose d'encore plus rare que de gagner plusieurs fois au loto !) Donc si on observe une telle série, on a une présomption très forte que quelque chose a agi qui n'était pas le hasard. Par exemple, la pièce était truquée.
Nous verrons diverses applications de cette idée générale dans le cadre des différents tests statistiques étudiés (par exemple test de comparaisons de moyennes, test du Chi², ...).
2.2. L'hypothèse nulle pour générer des expériences cruciales
Les philosophes ont depuis longtemps théorisé les mécanismes permettant l'induction, c'est-à-dire le processus par lequel on infère une cause générale à partir de l'observation d'effets particuliers. L'induction est un mode de raisonnement problématique, contrairement à la déduction. Cette dernière, sous réserve que les prémisses du raisonnement soient justes, et que le raisonnement ne soit pas entaché d'erreur, aboutit à une conclusion absolument certaine. L'induction n'offre pas cette garantie. Pour le dire simplement, le problème vient de ce que pour un ensemble d'observations données, il est possible de construire une infinité de modèles explicatifs pouvant éventuellement être incompatibles entre eux ! C'est pourquoi les scientifiques se trouvent souvent face à deux théories contradictoires (ou plus !). Ils doivent alors imaginer une situation telle que les prédictions des deux théories diffèrent. Il faut ensuite aller voir comment la réalité se comporte pour trancher en faveur de l'une ou l'autre théorie...
Cette stratégie, dite de l'expérience cruciale, trouve cependant sa limite lorsque l'on ne dispose pas de deux théories à opposer. Quand par exemple, lorsque l'on ne connaît encore rien sur le sujet... Que faire ?
Je peux tout simplement capitaliser sur le fait que je ne sais rien en postulant qu'en fait... il n'y a rien à savoir ! Comme aurait dit Coluche, "Allez hop ! Circulez, il n'y a rien à voir !" Autrement dit, postuler que seul le hasard est à l'œuvre dans le phénomène que j'étudie. Du coup, je peux opposer l'idée qu'il n'y a rien à savoir et l'idée que quelque mécanisme est à l'œuvre dans la construction de la situation1. Muni de ma théorie et de mon hypothèse nulle, je vais alors pouvoir comparer deux prédictions sur le devenir de la réalité : celle prévue par mon hypothèse nulle et celle prévue par la théorie.
_______________________________________________________
1. Ce quelque chose, le chercheur aura bien sûr envie de prétendre que c'est la cause prévue par sa théorie. Mais attention : montrer que le hasard explique difficilement les données ne suffit pas à établir positivement que la théorie du chercheur est la meilleure explication !
7.3. Le hasard agit-il comme une cause ?
Notons qu'une expression comme "l'effet du hasard" est un raccourci issu du langage courant mais tout à fait en désaccord avec la perspective scientifique sur la nature du hasard : contrairement à une représentation très répandue, le hasard n'est pas une entité magique qui assurerait la distribution équilibrée des événements, sorte de force de régulation qui ramènerait les choses vers un équilibre, une équité. Il serait beaucoup plus juste de concevoir le hasard scientifique, au contraire, comme une absence de détermination. C'est justement du fait de cette absence de détermination que les choses se répartissent à peu près équitablement.
En quoi cette précision est-elle importante ? Parce que si l'on conçoit le hasard comme une force, et que l'on constate qu'une série d'événements aléatoires semble aller dans un sens particulier (e.g., la pièce tombe toujours sur pile), alors on va tendre à croire augmentée la probabilité que les coups immédiatement suivants les choses vont s'équilibrer (la pièce va tomber sur face). Or, c'est faux ! Si je jette une pièce non truquée en l'air et qu'elle tombe dix fois sur pile, j'aurai peut-être envie de croire que le prochain coup face va plus probablement sortir... Et c'est faux ! Si la pièce est non truquée, les dix tirages précédents n'auront absolument aucun effet sur l'événement qui surviendra au prochain tirage, et la probabilité d'avoir pile au 11e tirage sera de nouveau 1/2. Mais des joueurs abusés par une conception du hasard comme force magique auront misé beaucoup plus gros qu'ils ne l'auraient fait autrement.
8. Population et échantillons
Objectifs. Positionner le vocabulaire et les concepts de base de la statistique inférentielle.
Prérequis.
- Cours de L1 sur les statistiques descriptives
Résumé. À partir du problème fondamental que pose la production de connaissances générales, on introduit les notions d'individu statistique, d'échantillon et de test d'hypothèse.
8.1. Le pari du développement de connaissances générales
On distingue classiquement les sciences dites "exactes", comme les mathématiques ou la logique, et les sciences dites "empiriques", comme la physique, la biologie, ou la psychologie. Contrairement aux premières qui ne requièrent qu'un bon cerveau et de bonnes stratégies de raisonnement, les sciences empiriques sont caractérisées par l'observation d'une réalité qu'il n'était souvent pas possible de penser a priori. Ou, pour être plus précis, qu'il est toujours possible de penser de différentes façons, incompatibles entre elles, mais entre lesquelles il n'est pas possible de trancher autrement qu'en allant observer le comportement de la réalité. Nous nous situons ici dans le cadre des sciences empiriques, au cœur même de ce qui en fait la difficulté : fonder la relation entre des modèles théoriques qui répondent idéalement aux canons des sciences exactes, et une réalité empirique plus ou moins compatible avec ces modèles.
Quelle que soit l'étude scientifique menée empiriquement, on a généralement un ensemble de données numériques, ou d'observations que l'on ramène à des nombres. L'analyse de ces nombres doit alors nous informer sur la structure de la réalité.
Le problème fondamental de la statistique est lié à la nature même de l'opération de quantification de la réalité. En effet, pour pouvoir quantifier la réalité, il faut l'observer. Il n'est généralement pas possible d'observer la totalité de la réalité, et donc on se ramène à l'observation d'une partie de la réalité. Mais la partie n'est jamais le tout. On fait alors le pari que la partie observée est suffisamment représentative du tout pour que ce que nous apprend notre observation de la partie soit utilisable pour comprendre aussi le reste de la réalité, bien plus vaste, que nous n'avons pas observé.
Mais voilà: qui dit pari dit risque de perdre. En l'occurrence pour le scientifique, risque de se tromper. Ce dernier étant prudent par nature va donc vouloir prendre un risque calculé. Il va vouloir évaluer le risque qu'il prend. C'est tout le sujet de la statistique inférentielle.
Bien entendu, la statistique inférentielle n'épuise pas le sujet de la question de la généralisabilité des conclusions prises à partir d'une observation restreinte de la réalité. Elle représente une tentative quantifiée d'évaluation du risque pris. À l'évidence, ce risque dépend fortement de la similarité entre la partie observée et la partie non observée. Ou, pour poser les choses autrement, entre la partie observée et le tout.
Nous allons maintenant voir comment la pensée statistique décrit ces réalités.
8.2. De l'échantillon à la population
2.1. Notion d'individu statistique
Notre scientifique va observer des exemplaires de son objet d'étude, exemplaires sur chacun desquels il prendra des mesures.
Nous appellerons Individu statistique chaque exemplaire de son objet d'étude. Pour un psychologue par exemple, un individu statistique peut correspondre à un individu humain. Ou encore à un couple, s'il étudie des couples. Ou s'il travaille en sciences de l'éducation, il peut très bien prendre une classe entière comme individu statistique. De l'autre côté du spectre, il peut même s'intéresser à un comportement particulier, le comportement d'appui sur un bouton, et prendre chaque exemplaire de ce comportement comme un seul individu statistique.
2.2. Échantillons d'individus et échantillons de mesures
Dans un premier sens du mot, on qualifiera l'ensemble des individus statistiques mesurés comme étant son échantillon .
Par opposition, on appellera population la totalité des individus qu'il aurait été possible d'observer dans l'absolu.
Admettons pour simplifier que notre chercheur ait pris une mesure par individu statistique. Il dispose donc d'un échantillon de mesures , ce qui constitue un deuxième sens du mot.
Il faut prendre garde à la distinction entre les deux : à partir d'un seul individu de l'échantillon d'individus, notre chercheur peut très bien prendre tout un échantillon de 100 mesures ! Ainsi, dans une approche de type avant-après (par exemple, on mesure chaque individu avant, puis après, l'application d'une thérapie), on disposera d'un échantillon d'individus, mais de deux échantillons de mesures, celles prises avant et celles prises après.
2.3. Décrire l'échantillon, mais inférer la population
Munis de ces définitions, reprenons notre problème initial. Nous l'avons vu en introduction, la partie de la réalité observée n'est généralement qu'une toute petite partie de la réalité totale. Le problème du chercheur est de quantifier le risque qu'il prend en supposant que les conclusions tirées à partir de l'échantillon s'appliquent à toute la population.
Il n'existe aucune expérience de psychologie ou de biologie qui prenne comme échantillon la totalité des humains. C'est tout simplement infaisable. L'échantillon est donc toujours différent de la population, c'est un sous-ensemble de la population.
Dans le cours sur la statistique descriptive, nous avons vu un ensemble de calculs qu'il était possible de faire pour décrire la réalité de nos échantillons. On peut par exemple calculer des indices de tendance centrale (moyenne, médiane) ou au moins de dominance (mode). On peut aussi produire des statistiques de dispersion (variance, écart-type, erreur standard, écart interquartile, ...). Etc. Mais absolument toujours, ce sont des valeurs calculées à partir de l'échantillon. Et donc toujours se pose la question du pari calculé ! Quel risque est-ce que je prends si je considère que ma statistique descriptive s'applique au-delà de mon échantillon ?
On dira donc que l'échantillon est décrit mais que la population n'est qu'inférée, imaginée à partir de l'échantillon. Et c'est pourquoi l'on parlera de statistique inférentielle dès lors qu'on veut généraliser nos résultats à la population entière.
8.3. Faiblesses de l'échantillonnage
On s'en doute, le terme d'échantillonnage traduit l'opération par laquelle on extrait un échantillon d'individus de la population cible pour procéder à des mesures. Si l'échantillonnage était parfait, on ne prendrait aucun risque en extrapolant à la population les conclusions tirées sur l'échantillon. Mais voilà, un échantillon n'est JAMAIS parfait. Examinons quelques faiblesses de l'échantillonnage.
3.1. Les biais d'échantillonnage
Les chercheurs en sciences sociales le savent bien, la population n'est pas homogène. Il y a des femmes, il y a des hommes. Il y a des grands et des petits, des gros et des minces, des jeunes et des âgés, des gens intelligents et d'autres qui le sont moins, des gens cultivés d'autres qui le sont moins, certains parlent français, d'autres anglais, etc.
Si l'on imagine qu'un échantillon parfait puisse exister, il faudrait donc que cet échantillon contienne la même proportion d'individus de chaque catégorie que la population globale. Le lecteur peut facilement se convaincre qu'il s'agit d'un exercice impossible si l'on considère la multitude de catégories qu'il est possible de prendre en compte.
On va donc parler de biais d'échantillonnage pour décrire une différence systématique entre l'échantillon et la population. Ces biais constituent évidemment des limites à la généralisabilité des résultats issus de la description de l'échantillon. Si mon échantillon est composé uniquement d'hommes, est-ce que les résultats de mon étude s'appliquent aussi aux femmes ? Peut-être... mais peut-être pas. Seule une réflexion menée au cas par cas permet d'évaluer ce type de risque et là, la statistique quantifiée n'y peut rien. Seule la connaissance du domaine peut donner une idée. Si j'étudie un thème neutre sexuellement, alors il est possible que les résultats obtenus sur des hommes soient valides sur l'ensemble de la population. Si au contraire, mon thème est fortement sexué, alors il est peu probable que mes résultats se généralisent, et à tout le moins, c'est à moi d'en établir la preuve, par exemple en répliquant mon étude sur un autre échantillon contenant des femmes.
3.2. Les erreurs d'échantillonnage
Même si le problème est simple, il reste que la population est incroyablement diverse alors que l'échantillon est réduit. Intrinsèquement, l'échantillonnage opère une réduction de la complexité de la réalité. Plus mon échantillon est petit par rapport à la population et plus cette réduction est importante.
Une différence majeure entre les notions d'erreur d'échantillonnage et de biais d'échantillonnage réside dans le caractère systématique de la faiblesse. En effet, si mon échantillon contient plus d'hommes que de femmes, alors que dans la population c'est l'inverse, je biaise systématiquement les résultats dans le sens d'un poids trop important donné aux informations tirées des hommes. Bien sûr, si en tant que chercheur je produis un tel biais par inattention, on aura envie de parler "d'erreur", conformément à l'usage du sens commun. Mais ce n'est pas le sens que l'on utilise lorsqu'on parle d'erreur en statistique. Dans ce dernier cas, on applique généralement le terme "erreur" aux situations où c'est le hasard qui est responsable des décalages entre la description de l'échantillon et la réalité de la population.
Comme le statisticien s'intéresse à des statistiques (moyenne, écart-type, etc.), on réservera le terme d'erreur d'échantillonnage aux décalages induits par l'opération d'échantillonnage sur ces statistiques. Et comme on veut s'y intéresser d'une manière générale, indépendante des spécificités de telle ou telle discipline, nous allons nous intéresser aux décalages qui ne dépendent que des propriétés mathématiques des mesures prises, notamment du fait des aléas.
8.4. Statistiques d'échantillon et statistiques de population
4.1. Statistiques de population
Si l'on en avait la possibilité physique, on pourrait construire une valeur mathématique, une statistique sur la population globale. Par exemple la taille moyenne. Il "suffirait" de mesurer les 8 milliards d'humains, entrer les mesures dans une gigantesque opération et en sortie l'ordinateur nous dirait sans difficulté quelle est la vraie taille de l'humain moyen (lequel n'existe pas, mais la question du rapport entre les construits de la science et leurs contreparties empiriques supposées sort du cadre du présent cours).
Nous aurons donc obtenu une Statistique de population, une mesure valable pour l'ensemble de la population. On note généralement ces statistiques avec des lettres grecques, ce dont on peut se servir comme moyen mnémotechnique pour rappeler leur caractère "idéal" plutôt que réel.
Typiquement, les moyennes de populations par exemple se notent avec la lettre grecque mu qui, en minuscule, s'écrit  .
.
Les écarts-types de populations se notent avec la lettre grecque sigma qui, en minuscule, s'écrit 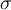 .
.
L'écart-type étant la racine carrée de la variance, les variances de population se notent souvent  .
.
À titre d'exemple, nous prendrons la population des hommes ayant marché sur la lune. À ce jour, cette population est très restreinte puisqu'elle comporte en tout et pour tout... 12 individus. Imaginons que nous nous intéressions à l'âge des individus de cette population au moment de leur sortie sur notre satellite. Nous obtenons le tableau suivant :
| Individu | Age |
| 1 | 38 |
| 2 | 39 |
| 3 | 39 |
| 4 | 37 |
| 5 | 47 |
| 6 | 39 |
| 7 | 39 |
| 8 | 41 |
| 9 | 41 |
| 10 | 36 |
| 11 | 38 |
| 12 | 37 |
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des âges, soit
et
On a aussi la variance de notre population qui est 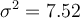
4.2. Statistiques d'échantillon
De même que l'on calcule les statistiques de population en prenant en compte tous les individus de la population cible, on calcule les statistiques d'échantillon en prenant en compte tous les individus de l'échantillon.
Pour chaque échantillon, on pourra donc calculer, par exemple, sa moyenne. On note généralement ces statistiques avec des lettres romanes. Typiquement, les moyennes d'échantillon par exemple se notent avec la lettre m (notez l'italique, correspondant aux normes de notation en vigueur en psychologie).
Il faut noter que pour des raisons techniques, la variance d'un échantillon se calcule avec une formule légèrement différente de la variance de la population : on divise la somme des carrés des écarts à la moyenne par n-1 et non par n.
Pour les besoins de l'exemple, imaginons que nous souhaitions connaître l'âge moyen des astronautes au moment de leur sortie, mais que nous ne disposions que des données pour un échantillon de 4 des 12 astronautes, les âges des autres nous étant inaccessibles. La meilleure estimation possible de l'âge moyen de la population serait donc l'âge moyen dans l'échantillon. Et la meilleure estimation possible de l'écart-type de la population serait l'écart-type de l'échantillon. Soit donc notre échantillon :
| Individu | Age |
| 4 | 37 |
| 5 | 47 |
| 6 | 39 |
| 7 | 39 |
À partir de ce deuxième tableau, il est facile de calculer les formules de la moyenne et l'écart-type des âges (revoir cours de première année), soit
Rappelons encore une fois que, pour des raisons mathématiques, on considère que l'estimation de la variance de la population à partir de la variance de l'échantillon est meilleure si l'on divise la somme des carrés par n-1 au lieu de n comme c'était le cas pour la variance de la population.Bien entendu, on imaginant que la moyenne de la population est à peu près comme la moyenne de l'échantillon, on commet une erreur d'estimation puisque cela nous conduit à évaluer l'âge de la population à 40.5 ans alors que, dans ce cas très particulier, nous savons que la vraie valeur est 39.25. Il en est de même pour la variance et l'écart-type : nous commettons des erreurs d'estimation. D'ailleurs, si nous tirons un autre échantillon, nous obtiendrons certainement des estimations légèrement différentes.
Et voilà posé un problème de la statistique : comment évaluer l'erreur commise sur l'estimation des caractéristiques de la population à partir des informations connues de l'échantillon ?
Une première idée est que les échantillons que l'on peut tirer d'une population constituent un ensemble que l'on peut étudier pour en inférer des informations sur la population. Examinons donc les relations qui existent entre les propriétés de la population et les propriétés de l'échantillon que l'on peut en tirer. La première des relations que nous allons considérer est la question du nombre d'échantillons que l'on peut tirer d'une population.
4.2. Dénombrement des statistiques d'échantillon
4.2.1. Premier facteur : la taille de la population
Soit une toute petite population d'individus, disons par exemple notre population d'individus ayant marché sur la lune. Nous l'avons vu plus, haut, chaque échantillon sera plus ou moins biaisé par rapport à la population. De plus, il y a de nombreuses façons de constituer l'échantillon.
Pour ceux qui ont le goût des mathématiques, on peut facilement dénombrer ces façons, car cela correspond au nombre de combinaisons de k individus que l'on peut tirer dans une population de n individus. Soit
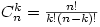
où le caractère "!" représente l'opération factorielle.
Par exemple, si nous appliquons cela à une population de, disons, 12 astronautes, et que l'on construit des échantillons de 4 personnes, le nombre d'échantillons possibles est
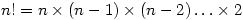
Et cela monte très très vite : avec une population de seulement 15 astronautes, on pourrait déjà tirer... 1365 échantillons de quatre individus !
4.2.2. Second facteur : la taille de l'échantillon
Le nombre d'échantillons différents que l'on peut extraire d'une population dépend d'un deuxième paramètre, à savoir la taille des échantillons, traduite par la lettre k dans la formule générale :
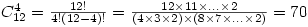
Un tableur nous donne directement la valeur cherchée au moyen de la formule suivante :
=COMBIN(n;k)
Sur une population de n sujets, on ne pourra construire qu'un échantillon de n sujets, mais on pourra construire n-1 échantillons différents de n-1 sujets. Dans l'exemple précédent, on voit facilement qu'on peut tirer 1365 échantillons de 4 sujets à partir de 15, mais on peut tirer 3003 échantillons de 5 personnes, 6435 échantillons de 7 personnes, etc. Au total, à partir de seulement 15 personnes, on peut tirer... 32767 échantillons différents !
4.2.3. Échantillonner c'est comme jouer au loto !
En fait, si l'on combine les deux facteurs précédents, on voit que de façon générale, il y a 2n façons différentes d'échantillonner une population de n individus. Partant de là, on voit que s'il s'agit d'étudier 8 milliards d'humains, le nombre d'échantillons possibles défie complètement l'imagination.
Et ne parlons même pas d'espérer réaliser l'échantillon parfait, celui qui serait parfaitement représentatif de la réalité complète. Il s'ensuit que tout échantillonnage réalisé dans la pratique peut s'apparenter à une sorte de tirage au sort dans une gigantesque urne décrivant tous les échantillonnages possibles.
9. La décision statistique
Objectifs. Introduire à la formalisation de la décision statistique.
Prérequis.
Résumé.
L'article pose les bases de la conception formelle de la décision statistique. On revient brièvement sur l'hypothèse expérimentale et l'hypothèse nulle. On définit en quoi consiste la décision statistique. Il s'agit aussi de définir les chances d'erreurs si la décision est mauvaise, ce que l'on appelle formellement les risques 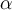 (alpha) et
(alpha) et 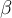 (beta), et introduire l'idée que l'on peut calculer les probabilités associées, c'est-à dire la probabilité pour chacun de ces deux risques, de se réaliser. On note alors
p
la valeur de la probabilité de se tromper en rejetant l'hypothèse que le hasard explique les résultats, et l'on se donne un seuil de signification pour considérer cette probabilité comme acceptable ou non.
(beta), et introduire l'idée que l'on peut calculer les probabilités associées, c'est-à dire la probabilité pour chacun de ces deux risques, de se réaliser. On note alors
p
la valeur de la probabilité de se tromper en rejetant l'hypothèse que le hasard explique les résultats, et l'on se donne un seuil de signification pour considérer cette probabilité comme acceptable ou non.
9.1. On part de l'effet observé

La décision statistique consiste fondamentalement à décider provisoirement si on peut considérer qu'une observation expérimentale donnée est le fruit du hasard ou bien résulte d'un mécanisme systématique.
Par exemple, l'observation expérimentale peut être que des enfants qui regardent beaucoup la télévision (qu'on appellera ici le "groupe expérimental") ont une plus faible capacité de concentration que des enfants qui la regardent peu ou pas (groupe que l'on qualifiera de "contrôle"). Dans cet exemple, on va peut être observer que les enfants du groupe contrôle résistent plus longtemps à une distraction pendant qu'ils travaillent sur un problème de maths que les enfants du groupe expérimental.
La différence mesurée entre les capacités moyennes de concentration des individus des deux groupes est ce que l'on appelle "l'effet observé". C'est l'effet observé que vous avez appris à produire dans les cours de "statistiques descriptives" de niveau L1 (moyennes, corrélations, etc.)
9.2. Les causes de l'effet observé: hypothèse expérimentale et hypothèse nulle

Initialement, avant même de construire l'expérience, le chercheur pouvait avoir l'hypothèse qu'un mécanisme précis lié à la télévision induirait un certain type de résultats. En l'occurrence, on peut supposer que le système attentionnel des enfants qui regardent beaucoup la télévision se développe moins bien que celui des enfants qui ne la regardent pas, notamment du fait de la faible durée qui s'écoule en moyenne entre deux changements d'image. Cette nouveauté artificielle hypnotise en quelque sorte le spectateur au lieu de lui apprendre à se concentrer. De ce fait, on peut s'attendre à ce que si l'on compare deux groupes d'enfants, ceux qui regardent moins la télévision auront une meilleure capacité de concentration.
Admettons que, fort de son hypothèse, le chercheur a comparé les deux groupes d'enfants, et admettons qu'il a observé l'effet attendu d'après son hypothèse expérimentale.
Mais le chercheur qui observe des résultats compatibles avec son hypothèse ne peut s'arrêter là. Il doit convaincre les autres chercheurs (et lui-même !). Or, un chercheur qui défend une théorie concurrente, moins complaisant à l'égard des résultats, pourra toujours expliquer le fait observé (que l'on ne cherche pas ici à nier) en invoquant le seul effet du hasard. Par exemple, il dira qu'en constituant les groupes de sujets, l'expérimentateur a très bien pu prendre sans le vouloir des sujets ayant des capacités de concentration inégales. Ou bien encore, par pur hasard, un certain nombre d'enfants du groupe expérimental avaient moins bien dormi la veille que les enfants du groupe contrôle, ce qui a réduit leur performance. Une multitude de tels petits facteurs, la plupart inconnus, peuvent ainsi concourir, en ajoutant leurs effets, à ce qu'un groupe ait une meilleure performance que l'autre ce jour-là, sans qu'on puisse espérer que cet effet puisse être répliqué lors d'une expérience suivante. Cette hypothèse qui invoque le hasard est ce que l'on appelle l'hypothèse nulle.
9.3. Un pari pour ou contre l'hypothèse nulle

Puisque face à tout résultat observé, on peut donner au moins une autre explication que celle postulée par le chercheur lorsqu'il a construit son expérience, ce dernier ne peut se contenter d'avoir observé l'effet, même si celui-ci va dans le sens qu'il attendait. Dans notre exemple, le chercheur qui a observé une meilleure capacité d'attention dans le groupe contrôle doit décider si ce résultat correspond à une réalité répétable ou s'il ne s'agit que d'un pur effet du hasard, à savoir l'hypothèse nulle. Cette décision est ce que l'on appelle la décision statistique ou encore "statistique inférentielle", ou encore "inférence statistique".
Classiquement, qui dit analyse de décision dit analyse des enjeux. La décision statistique ne fait pas exception à cette règle. La décision statistique est affaire de science. Autrement dit, il s'agit de produire de connaissances. Puisque le scientifique doit convaincre ses pairs de la rationalité de sa décision, il lui faut trouver des arguments solides pour justifier qu'il choisit son hypothèse expérimentale ou bien l'hypothèse nulle pour expliquer les résultats. Mais les conséquences de l'hypothèse expérimentale et de l'hypothèse nulle ne se posent pas toujours aussi simplement qu'en termes de "réalité" ou "fausseté" d'une hypothèse intellectuelle...
Par exemple, imaginons des décideurs qui doivent décider de relancer ou non un programme nucléaire après une catastrophe type Fukushima, Tchernobyl, ou Three Miles Island. Les faits observés sont qu'en 50 ans plusieurs accidents majeurs sont arrivés sur la planète. L'hypothèse nulle serait donc que des causes inconnues et imprévues interviennent de temps à autre pour causer une catastrophe que l'on n'avait pas vu venir.
Dans ce cas particulier, les tenants du nucléaire essaieront de défendre l'idée que les accidents sont dus, non pas au hasard (celui-ci étant incontrôlable, les accidents seraient susceptibles de se reproduire) mais à des causes entièrement contrôlables et que justement l'on saura contrôler. Au contraire, les antinucléaires vont plutôt défendre l'hypothèse nulle, à savoir que l'on ne contrôle pas tout et que la probabilité d'occurrence des accidents observée jusqu'ici permet de prédire plusieurs autres accidents majeurs dans les 50 ans à venir si l'on ne change pas de technologie...
Tout l'objet des cours de statistique inférentielle est de vous enseigner comment prendre ce type de décision de la façon la plus rigoureuse possible. Apprendre à bien décider en quelque sorte.
Pour bien décider entre deux hypothèses, il faut s'intéresser à deux choses. La plausibilité de chaque hypothèse d'une part, et, l'exemple du nucléaire nous le montre, il faut évidemment prendre en compte l'ampleur des conséquences potentielles de la décision. Commençons par regarder comment ces dernières sont analysées.
9.4. Les conséquences potentielles de la décision

Nous venons de dire que le chercheur doit réaliser un pari. Il doit décider que l'hypothèse nulle est suffisamment plausible pour qu'on ne puisse pas l'exclure, ou au contraire il doit décider que l'hypothèse nulle doit être rejetée, laissant ainsi la place à d'autres explications, dont évidemment l'hypothèse expérimentale.
Comme tout pari, il peut réussir ou échouer. Les conséquences entre un pari réussi ou raté ne sont évidemment pas les mêmes.
Certaines conséquences sont de nature épistémique (liées à la connaissance elle-même), d'autres sont plus pratiques.
Conséquences épistémiques. L'hypothèse expérimentale est un modèle de la réalité. Si les faits expérimentaux vont dans le sens de ce que prédisait cette hypothèse, alors le chercheur peut se dire qu'il a peut-être appris quelque chose sur la réalité. S'ils ne vont pas dans le sens de son hypothèse, il a aussi appris quelque chose, moins enthousiasmant pour lui évidemment, à savoir que son hypothèse ne marche pas très bien. Si nous parlons de science pure, fondamentale, les conséquences à court terme ne sont qu'épistémiques. Par exemple, s'il s'est trompé en rejetant l'hypothèse nulle à tort, cela veut dire que ce chercheur va affirmer à la communauté des chercheurs que des résultats expérimentaux soutiennent son hypothèse. Certains vont peut-être le croire à tort, et perdre ainsi du temps dans leurs propres recherches. Autrement dit, une fausse croyance se fera passer pendant un moment pour une connaissance établie scientifiquement.
Autres conséquences. S'il fait de la connaissance médicale par exemple, la décision du chercheur de considérer comme hasard ou pas les conséquences négatives d'une technologie peut avoir de lourdes conséquences. Il va peut-être convaincre d'autres individus, voire toute une communauté, de ne pas utiliser tel ou tel vaccin qui en réalité aurait sauvé plus de vies qu'il n'en aurait coûté. Ou à l'inverse, autoriser tel médicament qui en fait avait des effets négatifs importants. Pour certaines technologies, les conséquences financières et humaines peuvent être vraiment lourdes. Par exemple, dans la décision de poursuivre ou non l'industrie nucléaire, il y a d'un côté des milliards d'euros en jeu, et de l'autre côté une probabilité peut-être faible (elle n'est en réalité pas connue) mais non nulle de destruction majeure de l'environnement à l'échelle planétaire.
9.5. Les risques de type I et II

Le monde dans lequel nous nous trouvons réellement n'est pas connu lorsque nous faisons ce pari. C'est précisément pourquoi c'est un pari. Au minimum, on peut néanmoins supposer que notre hypothèse nulle, si elle est formulée scientifiquement, ne pourra avoir qu'une et une seule de deux valeurs de vérité possibles : elle sera soit vraie, soit fausse.
D'un autre côté, les éléments de preuve que nous avons à notre disposition (les "faits probants"), qui en général consistent en une valeur numérique produite par un test statistique (valeur z, valeur t de Student,  , etc.) rendent l'hypothèse nulle plausible ou bien non plausible.
, etc.) rendent l'hypothèse nulle plausible ou bien non plausible.
Les différents cas qui se présentent à nous sont donc :
- d'une part, l’hypothèse nulle (généralement notée H0) est vraie (le hasard suffit à expliquer les résultats) ou fausse (un effet systématique a causé les résultats).
- D'autre part, le test statistique peut donner un résultat compatible avec H0 (suggérer que H0 est vraie) ou incompatible avec H0 (suggérer que H0 est fausse).
En croisant ces deux constats, on obtient le tableau à quatre cases suivant :
| Réalité | |||
|---|---|---|---|
| H0 est vraie | H0 est fausse | ||
| Décision | H0 est acceptée | OK | Erreur de type II |
| H0 est rejetée | Erreur de type I | OK | |
En revanche, on appelle
- risque alpha (aussi noté α) le cas où l'hypothèse nulle est vraie, mais que le test conduit à la rejeter. C'est-à-dire commettre ce qui s'appelle l'erreur de type I.
- risque beta (aussi noté β) le cas où l'hypothèse nulle est fausse, mais que le test conduit à l'accepter. C'est-à-dire commettre ce qui s'appelle l'erreur de type II.
* Dans un monde épuré... Car dans la "vraie vie", il n'y a pas que des enjeux épistémiques, mais aussi des enjeux pour les chercheurs (besoin de publier pour leur carrière), pour les entreprises qui les emploient et qui peuvent les empêcher de publier des résultats en défaveur de tel médicament, de telle méthode de production d'énergie, etc. À tel point qu'il est maintenant devenu une norme scientifique dans beaucoup de domaines de rendre publique dans l'article l'existence des "conflits d'intérêts" potentiels entre la recherche et les carrières des auteurs.
9.6. Notion de "valeur-p"

Idéalement, la décision statistique serait basée sur une évaluation du risque de se tromper si l'on rejetait l'hypothèse nulle, c'est-à-dire évaluer quelle est la probabilité de commettre l'erreur de type I. Mais cela, on ne le sait pas. Par contre, ce qu'on peut calculer c'est la probabilité -- en supposant l'hypothèse nulle vraie -- d'avoir les résultats qu'on a obtenus. Par exemple, reprenons l'exemple introductif de M. Magik qui lance trois fois la pièce sur pile ; comme il n'avait annoncé.
Par définition, on peut quantifier une probabilité comme étant le nombre de cas "favorables" (on devrait plutôt dire de "cas cibles", ce serait plus approprié dans les cas où l'on quantifie un risque d'erreur !) divisé par le nombre de cas possibles (ou le nombre de cas connus, si l'on évalue la probabilité empiriquement sur la base de faits connus). La probabilité d'obtenir par hasard un tel résultat (pile, pile, pile) sur 3 lancers est 1 sur 8 puisqu'il y avait huit possibilités de résultats. Donc la valeur p est ici 1/8 soit 0.125. Sous l'hypothèse nulle, il y avait 12.5% de chances d'obtenir un tel résultat. C'est moins d'une chance sur deux, mais cela reste en tout cas beaucoup trop élevé pour qu'on puisse affirmer qu'autre chose que le hasard a joué (que ce soit la pièce truquée ou un soi-disant pouvoir télékinétique).
La majorité des tests que vous verrez en cours de statistique inférentielle dans la suite de votre cursus consisteront essentiellement en un ensemble de recettes plus ou moins sophistiquées pour calculer ces valeurs p, selon le type d'expériences, selon le type d'hypothèse nulle, selon la nature des données disponibles, etc.
Notons que formellement la valeur p est la probabilité d'obtenir nos données D sachant que l'hypothèse nulle est vraie, ce qu'on peut noter avec les conventions vues au lycée 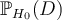 . En réalité, ce sont le chercheur aurait vraiment besoin pour sa décision, c'est la probabilité que l'hypothèse nulle soit vraie compte tenu des données disponibles,
. En réalité, ce sont le chercheur aurait vraiment besoin pour sa décision, c'est la probabilité que l'hypothèse nulle soit vraie compte tenu des données disponibles, 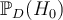 . Mais cela, attention, on ne l'a généralement pas !!
. Mais cela, attention, on ne l'a généralement pas !!
Mais alors, pourquoi nous intéresser à cette valeur p ? Parce que, intuitivement, plus ce nombre p est petit, et moins on a de chances de se tromper en rejetant l'hypothèse nulle. S'il y a une chance sur millle d'avoir un résultat comme on l'a eu si seul le hasard a joué, alors il devient difficile de croire que seul le hasard était à l'œuvre ! Bien sûr, cela reste néanmoins possible : même s'il y a moins d'une chance sur 1000 de gagner au loto, il y a pourtant régulièrement des gagnants. Cela nous amène à la question du seuil de la valeur p que l'on choisit comme acceptable ou non pour admettre un résultat scientifique comme valide...
Note : Vous pouvez aussi consulter notre article sur la façon de rédiger les valeurs p dans vos mémoires, devoirs, articles...
9.7. Seuil de signification de la valeur p

Comme l’hypothèse du hasard ne peut jamais être complètement éliminée (même très faible, cette hypothèse reste toujours possible), il faut donc se donner un seuil à partir duquel on considérera qu’il est raisonnable de rejeter l’explication du hasard. Concrètement, si la probabilité de l’hypothèse nulle est plus basse que ce seuil, on rejettera H0. Si cette probabilité est plus haute, on ne rejettera pas H0. C’est ce qu’on appellera le « seuil de signification ».
La question devient alors, comment définir adéquatement le seuil de signification ?
L'usage le plus courant est de prendre la valeur 0.05, c'est-à-dire qu'on considère qu'il est acceptable de rejeter l'hypothèse du hasard s'il y a moins de 5% de chances que le hasard explique les résultats qu'on a obtenus. Mais la valeur de ce seuil est nécessairement conventionnelle. Bien entendu, toutes choses égales par ailleurs, on souhaitera adopter le seuil de signification le plus bas possible, c’est-à-dire le plus proche de zéro possible. Ainsi, on pourrait se prémunir contre le fait de rejeter à tort l’hypothèse nulle car si on rejette H0, c’est vraiment que sa probabilité est très basse. Mais les choses ne sont pas si simples. En effet, les probabilités associées aux risques de types I et II fonctionnent en opposition : plus on baisse le risque de type I, plus on augmente celui de type II, et vice versa. Si je choisis un seuil de signification très proche de zéro, alors j’augmente le risque d’accepter H0 à tort. On ne peut donc pas baisser exagérément le seuil de signification conventionnel sous peine de commettre trop souvent l’erreur de type II et considérer à tort qu’un résultat est dû au hasard alors qu’en fait, il ne l’était pas. Par exemple si je jette en l'air trois fois une pièce truquée pour tomber toujours sur pile. J'obtiens (pile, pile, pile). Ce n'est pas par hasard, car la pièce est truquée. Mais au seuil de 5%, je ne vais pas rejeter l'hypothèse nulle car j'ai 12.5% de chance d'avoir obtenu ce résultat par hasard et que 12.5% > 5%. Et donc je vais commettre l'erreur de type II ! Alors comment choisir le bon seuil ?
Pour aller plus loin, il faut considérer les enjeux de la décision. Par exemple, si je veux juste produire une nouvelle connaissance scientifique, un risque de 5% est acceptable. Cela laisse 5% de risque d'énoncer une fausse vérité qui pourra tromper temporairement la communauté des chercheurs, mais d'un autre côté celle-ci est avertie, et va chercher à vérifier si le résultat est solide. Si, par contre, on est en train d'évaluer les conséquences secondaires négatives d'un vaccin que l'on peut potentiellement injecter à toute une population, et selon la gravité des conséquences négatives en question, 5% d'erreur peuvent devenir inacceptables. Il faudra donc alors baisser considérablement le seuil de signification, même si l'on sait que cela augmente le risque de type II dans le même temps (on risque de ne pas utiliser le vaccin à tort).
Examinons maintenant comment calculer la valeur p elle-même...
10. Évaluer la valeur p
Objectifs. Donner le principe général de calcul de la valeur p dans les différents tests
Prérequis. Article sur la statistique intuitive, Représentations graphiques des distributions, L'hypothèse nulle
Résumé. La valeur p est la probabilité" d'avoir un certain résultat descriptif si l'hypothèse nulle est vraie. Dans cet article, on commence par donner un exemple simple où l'on peut calculer directement cette valeur sans passer par la notion de distribution. Puis, on expose la logique générale de l'évaluation formelle de cette valeur telle qu'on la rencontre habituellement dans les tests statistiques.
10.1. Rappels préalables
A. Bref retour sur l'hypothèse expérimentale et l'hypothèse nulle.
Dans l'article sur l'hypothèse nulle, nous avons vu qu'il s'agit d'une prédiction faite sur le comportement d'une réalité donnée, prédiction ne supposant pas d'autre facteur actif qu'une simple répartition aléatoire, au hasard, des événements possibles. L'hypothèse alternative est l'hypothèse inverse : quelque cause systématique, peut être le mécanisme imaginé par le chercheur -- mais pas forcément --, est à l'œuvre. L'hypothèse du chercheur est donc un cas particulier de l'hypothèse alternative.
Malheureusement, dans les sciences expérimentales, les choses ne sont pas aussi simples que dans les sciences exactes, et l'on dispose très rarement d'une preuve directe en faveur d'une hypothèse, ou contre une hypothèse, mais seulement de faits qui sont plus ou moins compatibles avec l'un ou l'autre des deux hypothèses.
B. Bref retour sur l'erreur de type I et le risque  .
.
Une fois qu'il a recueilli ses données, le problème du chercheur est alors le suivant : comment, à partir d'un ensemble de données, évaluer à quel degré ces données sont compatibles avec ces deux hypothèses. Une fois cette évaluation réalisée, le chercheur devra encore décider s'il peut considérer l'hypothèse expérimentale comme acceptable ou si l'on doit considérer l'hypothèse nulle comme suffisante. Bien sûr, si l'hypothèse nulle est suffisante, cela va contre l'hypothèse expérimentale en vertu du principe de parcimonie puisque l'hypothèse nulle est, par principe, plus simple que l'hypothèse expérimentale : Si H0 n'est pas incompatible avec les données, il devient difficile de justifier de recourir à une hypothèse plus compliquée.
On voit donc que toute la problématique du test expérimental peut se ramener ultimement à un problème de décision de rejeter ou non l'hypothèse nulle*.
Puisqu'on est dans un problème de décision, et qu'il existe toujours des risques de se tromper, quatre cas sont possibles : je rejette H0 et j'ai raison; j'accepte H0 et j'ai raison; je rejette H0 et j'ai tort; j'accepte H0 et j'ai tort. Les deux derniers cas correspondent respectivement aux risques de types I et II respectivement.
Pour prendre la décision qui nous intéresse, on va donc chercher à réduire le plus possible le risque de type I. On se donne un seuil  et on exige que la
et on exige que la  pour nous autoriser à rejeter l'hypothèse du hasard. (le risque
pour nous autoriser à rejeter l'hypothèse du hasard. (le risque  est moins intéressant à considérer au niveau L2, mais il sert pour des cours plus avancés). Nous pourrons réduire le risque pris en rejetant l'hypothèse en choisissant un seuil bas pour la décision. Conventionnellement, on prend
est moins intéressant à considérer au niveau L2, mais il sert pour des cours plus avancés). Nous pourrons réduire le risque pris en rejetant l'hypothèse en choisissant un seuil bas pour la décision. Conventionnellement, on prend 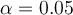 mais dans certaines situations le chercheur peut se donner un seuil encore plus bas, .01, .005, voire même .0005.
mais dans certaines situations le chercheur peut se donner un seuil encore plus bas, .01, .005, voire même .0005.
*Rappelons ici une fois de plus qu'on n'accepte jamais une hypothèse générale empirique
puisque l'on sait depuis Popper que les hypothèses générales ne peuvent
être que réfutées et jamais démontrées vraies. Et, par conséquent, on ne considère jamais que H0 est vraie, mais seulement qu'elle n'est pas réfutée, pas rejetée. À la rigueur, d'un point de vue décisionnel, on pourra la considérer comme provisoirement acceptable. Mais en aucun comme véritablement "acceptée".
C. Un exemple (très) simple du calcul du la valeur p.
Supposons que je veuille tester si une pièce est truquée. Je la jette, disons, 10 fois en l'air. Chacun sait que si elle n'est pas truquée, il y a une chance sur deux qu'elle retombe sur pile et une chance sur deux qu'elle retombe sur face. Une autre façon de le dire est de prévoir que si je jette la pièce en l'air 1000 fois, elle tombera environ 500 fois sur pile et environ 500 fois sur face. Cette prédiction ne fait appel à aucun autre mécanisme hypothétique que le seul « effet du hasard ». C'est donc un cas d'hypothèse nulle. À l'inverse, l'hypothèse que la pièce est truquée prédit qu'ultimement la pièce va tomber toujours sur pile ou toujours sur face (on pourrait avoir des trucages plus sophistiqués, mais admettons cela pour l'exemple).
Supposons maintenant qu'ayant lancé 10 fois la pièce en l'air pour tester l'idée qu'elle pourrait être truquée, j'observe 10 fois le résultat pile. La probabilité d'avoir 10 fois de suite pile par hasard peut se calculer facilement, car à chaque lancer j'ai une chance sur deux d'avoir pile. Les lancers étant supposés indépendants, les probabilités à chaque tirage se multiplient et j'ai donc ½×½×...×½, soit 1 sur 210 ; Autrement dit, il y a une chance sur 1024 d'observer un tel résultat si la pièce n'est pas truquée. Autrement dit, si l'hypothèse nulle est vraie, la probabilité d'avoir obtenu ce résultat est très légèrement inférieure à 0,001. Nous écrirons donc " p < 0,001 ". Ou encore si nous sommes dans un article scientifique conforme aux normes internationales de psychologie, "p<.001".
En apparence, c'est simple. Mais, seulement parce que nous sommes dans le cas très particulier où l'on sait calculer directement la probabilité d'avoir eu ce résultat en supposant que l'hypothèse nulle soit vraie. Nous allons maintenant étudier la procédure formelle de calcul qui s'applique dans le cas général qui s'appuie sur la notion de distribution.
10.2. La démarche générale du test d'hypothèse
Nous invitons les lecteurs aux articles de L1 sur les représentations des distributions pour réactiver leurs connaissances sur le sujet.A. La notion de distribution observée.
Dans l'immédiat, nous nous contenterons de rappeler qu'une distribution observée correspond grosso modo à la proportion d'observations qui tombent dans chacun des intervalles de valeurs possibles. Par exemple, si j'imagine un test d'aptitude intellectuelle comprenant 50 exercices, et que je compte un point par exercice réussi, chaque sujet obtient un score compris entre 0 et 50. Si je regroupe les valeurs possibles par intervalles de 5, cela me donne par exemple les intervalles 0-5; 6-10; 11-15 ; ... ; 46-50.
En pratique, on va par exemple constater que les individus dont le score tombe dans l'intervalle 0-5 ou 46-50 sont proportionnellement très rares. Au contraire, les scores qui tombent les intervalles 20-25 et 26-30 sont de loin les plus fréquents, représentant à eux seuls par exemple 50% des observations.
Nous avons donc là une distribution observée.
B. La notion de distribution théorique.
Supposons, que l'on sache que dans une situation donnée, un effet quelconque résulte de l'accumulation d'un grand nombre de petits effets aléatoires. Par exemple, si l'on prend la capacité générale à résoudre des problèmes logico-mathématiques inconnus, on sait que cette capacité proviendra de la conjonction d'une multitude de petits facteurs comme la vitesse de circulation de l'influx nerveux dans le cerveau, le temps passé à s'entraîner sur ce type de problème, l'état de fatigue du sujet, le fait que ses parents possédaient eux-mêmes une certaine aptitude générale à traiter cette classe de problèmes, la qualité et la quantité de nourriture reçue pendant la grossesse de la mère, etc. Alors, on peut prouver mathématiquement qu'une telle conjonction de facteurs aléatoires produira une distribution de type normale ou gaussienne. Autrement dit, les observations que l'on pourra faire devraient se répartir selon une courbe en cloche dite courbe de Gauss.
Bien entendu, on peut avoir d'autres présupposés théoriques, et donc construire mathématiquement d'autres distributions théoriques. À chacune de ces distributions théoriques correspondent un ensemble de postulats de départ qui, s'ils sont respectés, induisent une distribution de la forme correspondante. Les plus connues pour nous étant probablement la loi du t de student, la loi du F de Fisher, la loi du Chi-deux.
C. La distribution théorique correspond à l'hypothèse nulle parfaite
Pour la suite de la démarche, nous allons partir du principe que la distribution théorique correspond à la distribution théorique de l'hypothèse nulle.
En effet, les lois théoriques ignorent totalement l'hypothèse expérimentale du chercheur et ne tiennent compte que d'une distribution aléatoire dans les conditions étudiées. Si l'on admet que les postulats d'une distribution théorique (ou loi) devraient s'appliquer dans la situation étudiée, nous pouvons alors associer directement la distribution théorique et la distribution que l'on observerait idéalement si l'hypothèse nulle était vraie.
Il nous reste à trouver un moyen de comparer la distribution théorique, qui représente l'hypothèse nulle, et la distribution observée, qui représente la réalité. La suite de la démarche va consister à calculer la probabilité d'avoir les valeurs observées dans l'hypothèse où la loi théorique est valide. Et nous pourrons alors utiliser cette probabilité comme mesure du risque alpha.
La clé de ce calcul consiste alors à observer que...
D. Les paramètres d'une distribution théorique peuvent être associés à une probabilité
D.1. Principe
Prenons l'exemple de la loi de distribution dite normale. On sait que la loi normale est caractérisée par deux paramètres, sa moyenne μ et son écart-type σ.
Connaissant ces deux paramètres, et sous l'hypothèse que la distribution est effectivement normale, on peut alors dire que 68% des observations seront comprises entre la moyenne moins la valeur d'un écart-type et la moyenne plus la valeur d'un écart-type. De même 95% des observations seront comprises dans l'intervalle de deux écarts-types autour de la moyenne. Ou, ce qui revient au même, que moins de 5% des observations seront situées à plus de deux écarts-types de la moyenne.
Là où l'information devient intéressante pour notre sujet, c'est que l'on peut raisonner aussi dans l'autre sens pour, à partir de la valeur d'une observation particulière, calculer la probabilité de rencontrer une telle valeur. Si cette probabilité est trop faible, on tendra alors à rejeter l'hypothèse nulle (le hasard explique difficilement qu'on ait observé cette valeur) et sinon on acceptera l'hypothèse nulle (le hasard pourrait facilement expliquer cette observation).
Ce type de raisonnement s'applique pour la loi normale mais aussi pour
toute autre loi dont on connait les paramètres : loi du t de Student,
Loi du F de Fischer, Loi du  ....
....
D.2. Exemple
Supposons que nous voulons savoir si notre échantillon de données a une distribution normale. On sait que la forme d'une distribution normale est symétrique. On peut donc calculer à partir des valeurs de l'échantillon une statistique qui décrit à quel point notre échantillon est asymétrique. Une asymétrie de 0 correspond à une distribution parfaitement symétrique, une asymétrie de 1 correspond à une déviation vers la droite, une asymétrie de 2 est encore plus biaisée à droite, une asymétrie de -3 est encore plus biaisée, mais à gauche, etc.
Cette statistique d'asymétrie suit elle-même une distribution normale, c'est-à-dire que si l'on calculait cette statistique pour une multitude d'échantillons tirés d'une distribution symétrique (par exemple, on extrait aléatoirement 1000 échantillons de données de la population symétrique, et on obtient donc 1000 valeurs de la statistique d'asymétrie), la distribution des valeurs d'asymétrie suivrait à peu près une courbe de Gauss de moyenne 0 et d'écart-type 1.
Or, pour une valeur donnée qui suit une loi normale, on peut savoir quelle est la probabilité de tirer par hasard une valeur, plus petite (ou inversement, plus grande), ou plus éloignée de la moyenne, ou au contraire plus près de la moyenne. Cette probabilité correspond aux pourcentages d'observations qui dans la distribution sont inférieures (resp. supérieures) ou plus éloignées (resp. plus près) du centre de la distribution. Nous renvoyons à l'article sur la représentation des distributions).
Partant de là, si notre échantillon donne une valeur d'asymétrie disons de 4, on peut calculer que la probabilité que notre échantillon soit issu d'une population symétrique est d'environ p =0,00006. Dans ce cas, il est difficile de croire que notre échantillon est issu d'une population symétriquement distribuée.
Voyons maintenant de plus près le calcul de probabilité associé à la fonction normale, car il va servir de modèle pour tous les autres calculs de probabilité.
10.3. Calculer la valeur p par la loi normale
A. Distribution normale d’un échantillon réel
Soit une variable V quelconque contenant une série de données. Cette variable a une moyenne m et un écart-type s. Elle a aussi une distribution, à savoir que les effectifs se répartissent d’une certaine façon sur l’ensemble des valeurs possibles. Ce que l’on voit classiquement au moyen d’un histogramme comme celui-ci-dessous, qui représente les 863 notes obtenues à l’épreuve de mathématique du concours d’entrée dans une grande école d’ingénieurs (Il s’agit de données réelles que nous avons entrées dans une variable nommée « Math »).
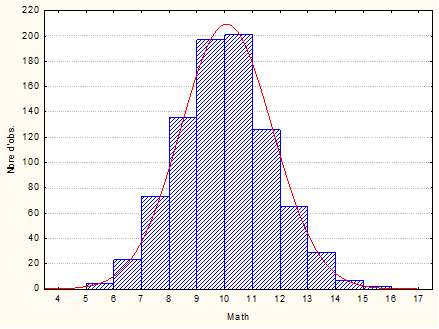
Sur l’histogramme, on voit ici apparaître en rouge l’allure de la courbe normale théorique la plus proche de la distribution de la variable V. Rappelons qu’une distribution normale théorique est caractérisée par deux paramètres, sa moyenne μ et son écart-type σ. Il suffit donc de connaître la moyenne et l’écart-type de l’échantillon pour connaître l’allure de la courbe normale qu’aurait la distribution de la population d’origine en supposant qu’elle soit normalement distribuée. Dans notre échantillon, La moyenne est m=10.0368 et l’écart-type est s=1.644482. On peut donc calculer la distribution théorique ayant ces caractéristiques-là et la comparer à la distribution observée dans l’échantillon.
Il va de soi que toutes les distributions d’échantillons ne sont pas normales, ne serait-ce que parce que les populations dont sont extraits les échantillons ne sont pas elles-mêmes toujours normales. Ainsi, par exemple, si l’on traçait la distribution des revenus en France, on obtiendrait une courbe tout à fait différente, ne serait-ce que parce que la distribution normale est symétrique autour de la moyenne alors que les revenus ne le sont pas.
On peut bien entendu s’interroger sur la meilleure façon de décider si une distribution d’échantillon peut être considérée comme normale ou non, mais nous le verrons plus loin. Pour le moment, nous admettrons que la présente distribution peut être considérée comme normale.
B. Obtention de notes z : la centration-réduction
Créons maintenant une nouvelle variable, appelée zMaths, par transformation de la variable Maths. Cette transformation sera ce qu’on appelle une standardisation, ou encore centration-réduction.
- La centration consiste pour chaque observation, à soustraire la valeur de la moyenne. Elle a pour effet que la nouvelle variable aura pour moyenne 0. Les observations qui dans l’ancienne variable avaient une valeur moindre que la moyenne vont se trouver avec des valeurs négatives tandis que celles qui étaient au-dessus de la moyenne vont se trouver avec des valeurs positives.
- La réduction consiste à diviser le résultat de la centration par la valeur de l’écart-type. Elle a pour effet que l’écart-type de la nouvelle variable est 1.
- Ainsi la nouvelle variable a pour moyenne 0 et pour écart-type 1. C’est que l’on appelle une « note z » et c’est d’ailleurs pour cela que l’on a appelé ici la nouvelle variable zMaths.
Voici l’histogramme de la variable zMaths :
Nous avons toujours le même nombre d’observations, mais la distribution est maintenant centrée sur 0 et le nouvel écart-type est 1, ce qui affecte l’aplatissement de la courbe mais pas la symétrie autour de la moyenne. D’ailleurs, si nous centrons-réduisons une variable non normale, la transformée ne sera pas normale non plus.
L’intérêt de travailler avec des notes z est que nous pouvons maintenant mettre directement les valeurs de la variable en relation avec les propriétés connues de la loi normale. C’est ce que nous allons faire, et cela va nous permettre de connaître les valeurs-p associées à un échantillon.
C. Obtention des valeurs-p à partir des notes z
Tout le raisonnement qui suit n’est valable que dans la mesure où la distribution de la population peut raisonnablement être considérée comme normale. Nous prendrons la moyenne de l’échantillon comme estimateur de la moyenne de la population, et l’écart-type de l’échantillon comme estimateur de l’écart-type de la population. À partir de là, puisque nous avons centré-réduit, nous pouvons considérer que notre variable zMaths constitue un échantillon extrait d’une population dont la moyenne est 0 et l’écart-type 1. Sous l’hypothèse que la distribution de la population globale est normale, nous pouvons donc assumer que la variable zMaths est distribuée comme une note z normale.
C.1. Rappel de quelques propriétés de la loi normale
Que savons-nous de la distribution des notes z ? Beaucoup de choses. Pour le comprendre nous allons examiner les propriétés de la courbe en rouge, que l’on appelle la fonction de « densité de probabilité ». La surface sous la courbe représente la façon dont les effectifs sont répartis.
La première propriété est la symétrie : la loi normale est symétrique autour de la moyenne, donc autour de 0 pour les notes z. Par conséquent 50% des notes seront en dessous de 0 et 50% seront au-dessus. Sur le graphique ci-dessous, la zone grisée représente la surface telle que les notes sont sous le critère X qui vaut ici zéro. La valeur p=.50 traduit le fait que 50% des observations se trouveront sous cette valeur.
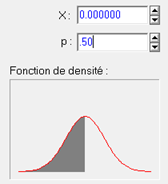
La symétrie à une autre conséquence : si nous prenons une valeur positive X quelconque, la probabilité d’avoir une note supérieure à X sera exactement égale à la probabilité d’avoir une note inférieure à -X. Dans l’exemple ci-dessous, nous avons pris la valeur +1. On voit que la probabilité d’avoir une note supérieure à +1 est p=.158655 (figure de droite). Si nous prenons la valeur -1 et que nous regardons la probabilité d’avoir une note plus basse, nous trouvons encore p=.158655 (figure de gauche ci-dessous).
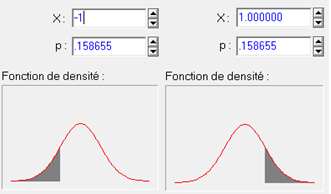
En les cumulant, on sait donc que la probabilité d’avoir par hasard une note dont la valeur absolue dépasse 1 (c’est-à-dire est plus grande que 1 ou plus petite que -1) est .317311 :
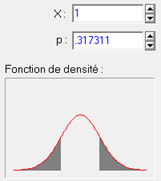
Il est très important de distinguer ce qui se passe à l’intérieur ou à l’extérieur de l’intervalle ainsi défini. En effet, comme on le voit sur la courbe, le centre de l'intervalle correspond aux valeurs compatibles avec le hasard. Plus on s’éloigne du centre et moins il est probable d’avoir obtenu la note par hasard. Si l’on a observé une valeur zobs et que l'on prend comme bornes de l’intervalle les valeurs –zobs et +zobs, les valeurs à l'intérieur de l'intervalle corroborent l'hypothèse nulle. Au contraire, celles à l’extérieur de l’intervalle sont les valeurs qui correspondent à un risque de se tromper en rejetant l’hypothèse nulle. Autrement dit, la surface sous la courbe à l’extérieur de l’intervalle est la probabilité que l’hypothèse nulle soit vraie compte tenu de la valeur z observée dans l’échantillon. C’est donc la valeur-p que nous cherchons pour l’inférence statistique. Plus elle est faible, ou ce qui revient au même, plus l’intervalle est grand, et plus le risque pris est faible.
Comment connaître la surface sous la courbe comprise à l’intérieur ou à l’extérieur de l’intervalle ?
Puisque la somme de toutes les probabilités fait 1.0 par définition, la région comprise entre les deux bornes -1 et +1 contient 100%-31,7%=68,3% des observations (p= .682689) :
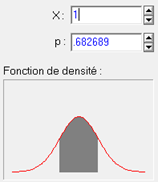
Par le même raisonnement, on trouve que 95.5% des observations sont comprises entre -2 et +2 (rappelons que pour des notes z, 1 signifie un écart-type et 2 signifie deux écarts-types). Autrement dit, il n’y a que 4.5% de chances d’observer par hasard une note z plus grande que 2 ou plus petite que -2.
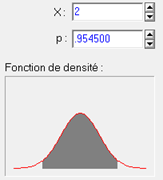
À l’inverse, puisque nous sommes intéressés par le seuil alpha de 5% qui caractérise conventionnellement la significativité, on peut se demander quelle est la valeur de z qui ne laisse que 5% des observations à l’extérieur. Il s’agit de 1.96 :
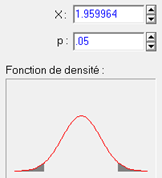
Donc si nous obtenons une statistique observée zobs, de type z (normale standardisée), dont la valeur absolue dépasse 1.96, nous avons un résultat significatif au seuil de 5%, autrement dit, il y a moins de 5% de chances qu’un échantillon ayant été extrait d’une distribution normale de moyenne 0 et d’écart-type 1 permette de calculer la note zobs. Nous dirons aussi que 1,96 est une valeur critique de z au seuil alpha de 5%.
On peut de la même façon calculer une valeur critique au seuil de 0.01 :
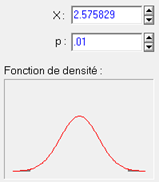
C.2. Test en unilatéral. Si l’on n’a qu'une hypothèse non directionnelle sur la valeur de z, on teste juste à quel point la valeur z observée s’écarte de 0, l'on doit prendre en compte pour le calcul de p, l’aire sous la courbe des deux côtés de la valeur critique (+z et –z). On le voit sur le graphique précédent par le fait que les deux queues de la courbe sont grisées. C’est pourquoi on qualifie un tel test de bilatéral. Mais supposons que l’on ait une hypothèse directionnelle. Par exemple, lorsque d'après l’hypothèse expérimentale, la valeur attendue de z est positive tandis qu’une valeur négative réfuterait l’hypothèse. Dans ce cas, il ne serait pas juste de compter comme représentant un risque les valeurs sous la courbe, mais seulement celles dans la queue opposée à l’attente de l’hypothèse expérimentale. Donc, et sous réserve que le résultat observé soit du côté prévu par l’hypothèse expérimentale, on peut retrancher du calcul final l’aire dans la queue du signe opposé au résultat attendu. Et puisque la distribution normale est symétrique, cela revient purement et simplement à diviser par deux la valeur-p qu’on avait obtenu en bilatéral. C’est alors un "test unilatéral". Cette possibilité peut ainsi faire passer un test du statut de non significatif en bilatéral (par exemple, p=.08) au statut de test significatif (car alors on a p=.08/2=.04 ce qui est significatif au seuil de 5%).
Il est important de savoir que la possibilité de travailler en unilatéral est subordonnée au caractère symétrique de la loi, faute de quoi, il n’y a plus aucune légitimité à diviser par deux la valeur-p obtenue.
10.4. Calculer la valeur p par le t de student, le chi-deux et le F
A. La loi du t de student
La distribution du t de student est légèrement différente de celle du z, car elle est dérivée de cette dernière en examinant la distribution des échantillons de taille n que l'on va extraire d'une distribution normale. Elle admet donc un paramètre supplémentaire : le nombre de degrés de libertés (ddl=n-1). On pourrait dire que la courbe de densité de probabilité du t de student est essentiellement une déformation légère de la loi normale et plus le nombre de degrés de liberté est grand, moins la déformation est prononcée.
De ce fait, une fois qu’on a renseigné le nombre de degrés de liberté, si l’on dispose d’une note t de student, l’utilisation est rigoureusement la même que celle d’une note z. Le graphique suivant illustre une loi du t de student à 30 degrés de liberté. On voit que la valeur critique pour alpha=.05 en bilatéral est atteinte pour un t de 2.04, ce qui n’est pas très différent du 1.96 que l’on avait pour les valeurs z.
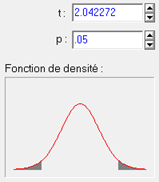
Si l’on a moins de degrés de liberté, la valeur critique augmente, et réciproquement. Avec 500 degrés de liberté et au-delà, la valeur critique tombe à 1,96 et converge ensuite lentement vers cette valeur.
B. La loi du  ("Khi deux" ou "Khi carré")
("Khi deux" ou "Khi carré")
Comme son nom l’indique, la loi du Khi-2 sert à tester une valeur observée du Khi-deux. Donc à calculer le risque pris si l’on décide de rejeter l’hypothèse nulle que les résultats soient le fait du hasard.
Cette distribution accepte un paramètre, le nombre de degrés de libertés. Rappelons que le chi-deux s’utilise lorsque l’on teste la répartition des effectifs dans une table de L lignes et C colonnes et que le nombre de degrés de liberté est alors (L-1)(C-1). En effet, plus la table est grande, et plus le chi-deux peut être élevé par pur hasard (car il y a plus de cases susceptibles de présenter des écarts entre effectifs observés et effectifs théoriques).
La figure suivante représente l’obtention de la valeur critique du chi-deux pour le seuil alpha=.05 avec 5 degrés de libertés (par exemple une table 2 lignes 6 colonnes). On voit que la valeur critique de khi-deux est 11.07 au seuil de p=.05.
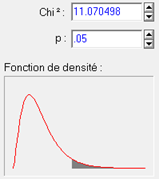
La figure suivante représente l’obtention de la valeur critique du chi-deux pour le même seuil alpha=.05 mais avec 10 degrés de libertés.
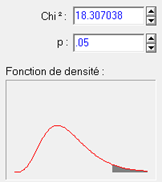
On voit que la valeur critique est maintenant de 18.30. C’est plus élevé qu’avec 5 degrés de liberté car contrairement à ce qui se passe dans l’utilisation des tables du t, le nombre de degrés de liberté ne dépend pas du nombre de sujets mais du nombre de cellules du tableau. Donc en dépit du même nom « degrés de liberté » les réalités sous-jacentes sont très différentes et influent différemment l’obtention des valeurs p.
Pour le reste, l’idée est la même qu’avec les lois normales et du t à ceci près que l’absence de symétrie empêche de distinguer les tests en unilatéral ou bilatéral : On ne s’intéresse ici qu’à l’extrémité droite de la courbe : c’est la surface à droite de la valeur critique du Chi-deux qui doit être la plus réduite possible si l’on veut pouvoir rejeter l’hypothèse nulle.
C. La loi du F
La loi du F accepte deux paramètres, qui sont encore des degrés de libertés. Le premier paramètre est de même nature que les degrés de liberté de la loi du chi-deux. En effet, le F sert à comparer des moyennes, comme le t, mais dans un cas où peut y avoir plusieurs facteurs, et chaque facteur peut lui-même avoir plus de deux modalités. Le croisement des modalités des facteurs constitue donc un tableau en soi et ce premier degré de liberté résulte de ce croisement. Toutefois, le mode de calcul étant différent, l’influence du nombre de degrés de libertés sur la détermination des valeurs critiques ne fonctionne pas comme pour le chi-deux.
Le second paramètre dépend du nombre d’observations concernées par le test. C’est donc un degré de liberté de même nature que celui le test du t. D’ailleurs, lorsque l’on teste un t à un seul degré de liberté (comparaison de deux groupes), la valeur de F est en réalité simplement le carré du t de student que l’on aurait en faisant la même comparaison. Afin de l’illustrer, vous pouvez comparer la figure suivante, où l’on a un seul ddl pour le premier paramètre et 30 pour le second. On trouve alors comme valeur critique 4.170877. Avec deux groupes et 30 sujets, il faut donc que la statistique F atteigne cette valeur au moins pour que le test soit significatif au seuil alpha=5%. Or, vous pouvez remarquer que la racine carrée de 4.170877 est 2.042272, ce qui est bien la valeur critique que nous avions obtenue pour le t de Student à 30 degrés de liberté.
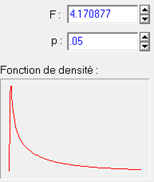
Si maintenant, nous étudions la valeur critique de la loi du F toujours au seuil de 5% et toujours avec 30 ddl comme second paramètre, mais 6 ddl comme premier paramètre (par exemple, nous testons un facteur à 7 modalités ou bien une interaction entre un facteur à 4 modalités et un facteur à 3 modalités) :
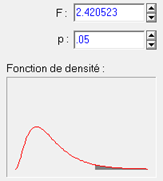
On voit bien que la distribution a changé de forme, tandis que la valeur critique est tombée à 2.42.
Comme dans le cas du  , l’absence de symétrie empêche de distinguer les tests en unilatéral ou bilatéral : On ne s’intéresse ici qu’à l’extrémité droite de la courbe : c’est la surface à droite de la valeur critique du khi-deux qui doit être la plus réduite possible si l’on veut pouvoir rejeter l’hypothèse nulle. C’est pourquoi lorsque l’on n’a que deux groupes à comparer et une hypothèse orientée, il vaut mieux utiliser un t.
, l’absence de symétrie empêche de distinguer les tests en unilatéral ou bilatéral : On ne s’intéresse ici qu’à l’extrémité droite de la courbe : c’est la surface à droite de la valeur critique du khi-deux qui doit être la plus réduite possible si l’on veut pouvoir rejeter l’hypothèse nulle. C’est pourquoi lorsque l’on n’a que deux groupes à comparer et une hypothèse orientée, il vaut mieux utiliser un t.
11. Questionnaire d'auto-évaluation
Ce QCM comprend 10 questions. Répondez à chaque question puis, à la fin, lorsque vous aurez répondu à toutes les questions, un bouton "terminer" apparaîtra sur la dernière question. En cliquant sur ce bouton, vous pourrez voir votre score et accéder à un corrigé.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte