Statistique : Tester l'association de variables

1.1. Nuage de points multidimensionnel

Lorsque nous voulons régresser une VD sur k prédicteurs, nous ne cherchons plus seulement à modéliser un nuage de points dans un plan (2 dimensions) mais plus généralement dans un espace à k dimensions. Par exemple, si nous ajoutons un nouveau prédicteur à la régression des articles précédents, F11VN, nous cherchons en fait à modéliser un nuage de points dans un espace à trois dimensions :

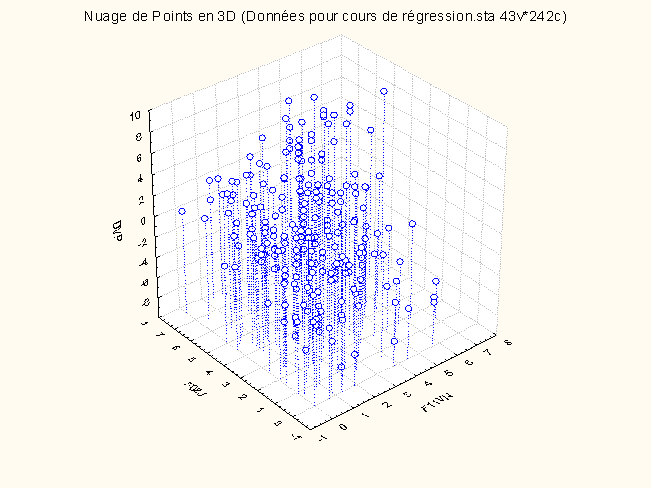
1.2. Ajustement multilinéaire

Le fait d’être dans un espace à k dimensions ne change pratiquement rien au fond des concepts vus plus haut. Ainsi, imaginons un espace à 3 dimensions, c'est-à-dire où chaque point est défini par sa valeur sur chacune des trois variables X₀ , X₁ et Y , l’équation de la droite qui s'ajustera le mieux au nuage de points dans cet espace s’écrira

Y = b₀ +  b₁ X₁ + b₂ X₂

Nous n’avons plus une « droite de régression » mais un « plan de régression » :

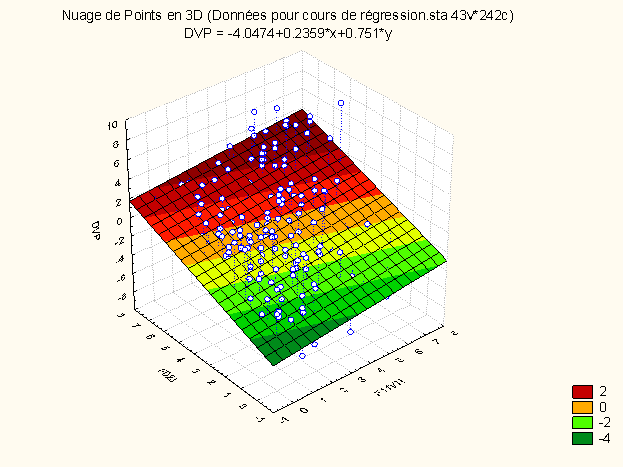
Ou encore plus généralement, dans un espace à k dimensions, nous avons un « hyperplan de régression » :

Y =  b₀ + b₁ X₁ + b₂ X₂ + … + b_k X_k

Cela devient franchement difficile à se représenter mentalement, mais cela n’a en pratique qu’une importance mineure, car les principes restent les mêmes.