Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
4. Régression linéaire multiple : coefficients multidimensionnels
4.2. Les coefficients de la régression multiple
Prenons l’exemple d’une régression à deux prédicteurs : DVP est la VD, F11VN et F02J sont les prédicteurs.
Nous obtenons :
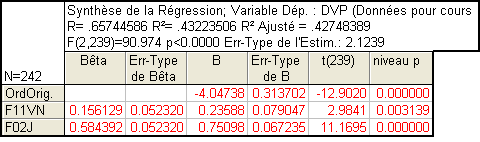
Ce tableau ressemble très fortement à celui de la régression simple mais appelle quelques commentaires.
Les B : Comme dans la régression simple, les coefficients B de la régression multilinéaire correspondent aux constantes qui définissent le poids de chaque prédicteur dans l’équation de régression.
L’équation ici est donc DVP = -4.048 + 0.236*F11VN + 0.751*F02J.
C’est l’équation du plan dans la figure vue plus haut.
Les bêtas : Comme dans la régression simple, ce sont les coefficients standardisés. On passe des β aux b par la relation
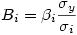
où σ y et σ i représentent les écarts-types de la VD et de la VI, respectivement.
On passe des b aux β par la relation inverse
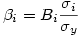
Attention :Il s’agit des écarts-types de la population et non des écarts-types corrigés (ce qui explique qu’on les note ici σ et non s).
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte
