Statistique : Tester l'association de variables
 Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales ( de Spearman,
de Spearman,  de Kendal), ou nominales (
de Kendal), ou nominales ( et
et  ). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
5. Régression linéaire multiple : Ajustement du modèle
Objectifs. Apprendre à réaliser concrètement une régression linéaire multiple avec un logiciel de statistique. Présentation de l'évaluation de la qualité globale du modèle obtenu.
Prérequis.
- Cours de L1 sur la corrélation linéaire
- Cours de L1 sur l'Approche intuitive
- Cours de L1 sur la statistique inférentielle, l'Hypothèse nulle
- La décision statistique
- Test de la liaison entre deux variables : descriptive L1 / Inférentielle L2
- Régression simple approche descriptive (L1)
- Régression simple : approche inférentielle (L2)
Résumé. L'article part du principe que l'étudiant dispose d'un logiciel de statistique pour réaliser les calculs. On présente les traitements à réaliser et comment interpréter les principales données produites par les logiciels.
Le R² : Dans une régression multilinéaire, le R²fournit la part de variance expliquée par l’ensemble des prédicteurs :
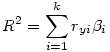
β i est le bêta du i ème prédicteur et ryi le coefficient de corrélation entre ce prédicteur et la VD.
Dans l’exemple précédent (F11VN et F02J qui prédisent DVP), si nous prenons la matrice de corrélations des variables impliquées :

et que nous appliquons les bêtas obtenus dans la régression précédente
Nous obtenons R² = (.369*0.156)+ (.641*0.584)= 0.432, ce qui est bien le R ² annoncé dans cette régression.
R-deux ajusté : Comme nous l’avons dit à propos de la régression simple, c’est une valeur de R corrigée pour réduire un biais lié au fait que chaque prédicteur supposé peut expliquer une partie du nuage de points par le seul fait du hasard. Or, ce biais augmente avec le nombre de prédicteurs. Si n est le nombre d’observations et k le nombre de prédicteurs (sans compter la constante),
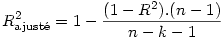
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte

