Statistique : Tester l'association de variables

Elle consiste à introduire les variables une par une. À chaque étape, le modèle comprenant l’ensemble des VI sélectionnées est alors recalculé avec la méthode standard.

Analysons la sortie de SPSS obtenue avec les données de l’exemple précédent, mais en adoptant la méthode pas à pas. 

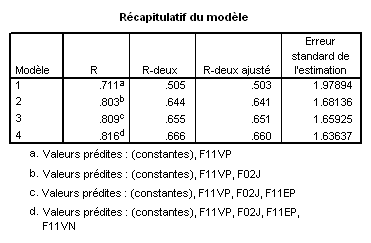
On voit ici que 4 modèles ont été construits successivement.

On peut remarquer que l’ordre d’introduction des variables correspond à l’ordre d’importance des contributions relatives tel qu’il apparaissait dans la méthode standard.

On peut aussi remarquer que le processus s’arrête avant l’introduction de la variable F11EN : celle-ci contribue tellement peu qu’elle n’atteint pas le critère d’introduction dans un nouveau modèle. Ce critère est un paramètre que le chercheur peut fixer. Généralement, on utilise le seuil classique de p = .05. Il faut noter ici que, comme pour toutes les méthodes d’analyses statistiques, une contribution non significative ne signifie pas forcément absence de contribution. Il se peut que la variabilité des données soit simplement trop grande devant la taille de l’effet de la variable pour que le test de signification puisse détecter cet effet. La même analyse conduite avec un nombre beaucoup plus élevé de sujets conserverait peut-être cette variable.

Fort logiquement, le R ² ajusté des modèles augmente avec chaque variable introduite, et tout aussi logiquement, cette augmentation est de plus en plus faible avec l’introduction de variables de moins en moins contributives.

Il est crucial de remarquer ici la différence d’évolution des valeurs de R² et de R² ajusté. Le R² ne diminue jamais avec l’augmentation du nombre de VI. Il n'en va pas de même pour le R² ajusté. Au contraire, si l’on compare le modèle 4 de ce tableau avec le modèle donné dans l’exemple de la méthode standard, nous voyons que la prise en compte de la variable F11VN dans la méthode standard n’a strictement rien ajouté à la capacité prédictive brute du modèle : le R² est le même (.666) dans les deux cas. Toutefois, le R² ajusté est meilleur dans le modèle obtenu dans ce cas par la méthode pas à pas. Ceci traduit tout simplement le principe de parcimonie (le fameux « rasoir d’Occam ») : le modèle avec moins de VIs est plus parcimonieux, et puisqu’il a le même pouvoir de prédiction, il est donc meilleur. 

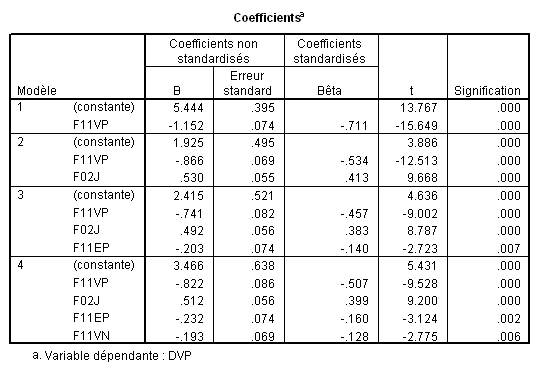
L’analyse du tableau des coefficients montre bien que les coefficients d’une même variable changent selon le modèle considéré. Par exemple, la variable F11VP a un bêta de -.711 lorsqu’elle est seule, mais il tombe à -.534 lorsqu’il est calculé en même temps que la variableF02J.