Statistique : Tester l'association de variables

3.1. Présentation du problème

Une première approche consiste à produire le nuage de points que l’on obtient en prenant les valeurs prédites comme abscisses et les résidus comme ordonnées.

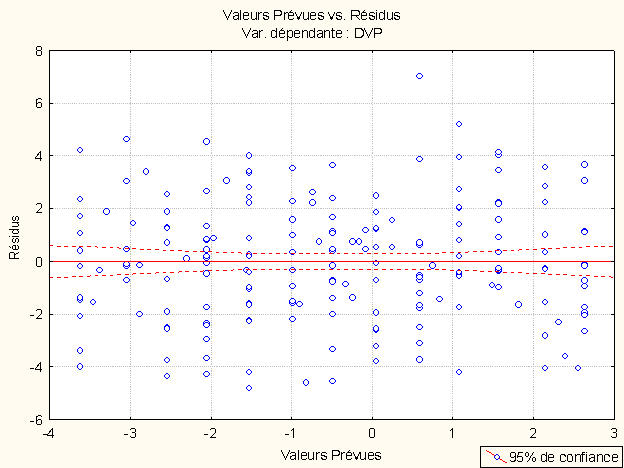
Selon Tabachnick et Fidell (1996), « si toutes les assomptions sont remplies, les résidus seront distribués presque rectangulairement avec une concentration de scores le long du centre » (p. 137). On peut bien sûr dessiner des cas d’école mais, sur de vraies données, comme on le voit sur notre nuage de points, tout le problème est de savoir ce que l’on entend par « presque » !!

3.2. Définitions

L'homoscédasticité s'observe lorsque la dispersion des résidus est homogène sur tout le spectre des valeurs de la VI. C'est une propriété souhaitable puisque si les résidus correspondent bien à des aléas de mesure, il n’y a pas de raison que la dispersion de ces résidus change en fonction des valeurs du prédicteur.

Si la dispersion des résidus n’est pas homogène, on parle d’hétéroscédasticité. Sur le schéma précédent, la dispersion des résidus autour des valeurs prédites est symbolisée par les deux courbes pointillées autour de la droite. Idéalement, ces courbes devraient être parallèles à la droite.

L’analyse de l’homoscédasticité est l'équivalent, pour les prédicteurs continus d'une régression, de l’analyse de l’homogénéité des variances entre les groupes dans une ANOVA ou un test de student (par exemple au moyen d'un test de Levene).  

3.3. Origines de l'hétéroscédaticité

L’hétéroscédasticité apparaît 

• si l’une des deux variables n’est pas normale.
• s’il existe une relation particulière entre les deux variables. Par exemple, une relation entre l’âge et le salaire : plus les gens avancent en âge et plus il y a de variations dans les salaires.
• si l’erreur de mesure change selon les niveaux des variables

Par exemple, si à un certain âge les gens sont plus concernés par leur poids, ils en donneront des estimations plus fiables que celles des gens moins ou plus âgés. La variance des estimations données par les individus sera donc plus faible aux valeurs moyennes de la pyramide des âges qu’aux extrêmes. 

Pour la régression linéaire, il me semble que le test de l’homoscédasticité est essentiellement utile à la compréhension de la structure des données (nécessité de transformation, etc.)