Relation d'équivalence

Objectifs : définir le concept de relation d'équivalence, fondamental pour la classification des éléments d'un ensemble ; définir les concepts associés de partition et d'ensemble quotient.
Prérequis : aucun.
Utilisé comme prérequis dans les articles : Échelles de mesure
Résumé :
une relation d'équivalence  est une relation binaire définie sur un ensemble E.
est une relation binaire définie sur un ensemble E.  est réflexive, symétrique et transitive.
est réflexive, symétrique et transitive.  définit une partition de E. L'ensemble quotient E/
définit une partition de E. L'ensemble quotient E/ est l'ensemble des parties de E induites par
est l'ensemble des parties de E induites par  .
.
rédaction : Stéphane Vautier
1. Définitions
Les éléments de définition qui suivent sont empruntés à Barbut et Monjardet (1970a). On considère un ensemble E composé d'au moins deux éléments distincts. On considère une relation binaire R permettant de mettre les éléments de E en relation.
La relation  est une relation d'équivalence si elle possède les trois propriétés suivantes :
est une relation d'équivalence si elle possède les trois propriétés suivantes :
- pour tout x de E,
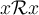 : réflexivité ;
: réflexivité ; - pour tout x, y de E,
 : symétrie ;
: symétrie ; - pour tout x, y, z de E,
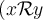 et
et  : transitivité.
: transitivité.
La classe d'équivalence d'un élément x de E est la partie de E formée de tous les éléments qui sont en relation avec x. Les parties de E obtenues comme classe d'équivalence d'un élément x de E sont les classes d'équivalence induites par  . Ces classes d'équivalence forment une partition de E. L'ensemble quotient, noté E/R, est l'ensemble des classes d'équivalences induites par
. Ces classes d'équivalence forment une partition de E. L'ensemble quotient, noté E/R, est l'ensemble des classes d'équivalences induites par  .
.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte

