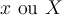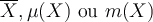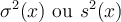Résumé de section

◄Savoir Faire
►Références

  • La rubrique « Rappels de maths » est une aide destinée à rappeler certaines notions mathématiques de base qui ont pu être oubliées.

    L'étudiant trouvera ici une approche de ces concepts sur plusieurs niveaux. Les articles listés plus bas constituent les points d'entrée principaux, mais certaines démonstrations sont aussi disponibles depuis l'intérieur des articles pour ceux qui souhaitent consolider leur maîtrise des outils mathématiques de base.

    • Conventions de notation Livre

      x \text{ ou } X ? x \text{ ou } X ? \overline{X}, \mu(X)\text{ ou } m(X) ? \sigma^2(x) \text{ ou } s^2(x) ?

      Objectifs. Énumérer les conventions de notation utilisées dans ce cours.

    • Fonction affine Livre

      Objectifs : Rappeler ce qu'est une fonction affine.

      Pré-requis : aucun.

      Utilisé comme prérequis dans les articles :

      Résumé. Une fonction affine est une fonction de type f(x)=ax+b

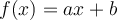
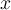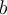      où x appartient à un sous-ensemble de l'ensemble des nombres réels, a , le coefficient directeur de la droite représentative est un réel, et b, l'ordonnée à l'origine, est un réel. 
      Ce concept est exemplifié par une animation.
    • Moyenne Livre

      Objectif. Définir la moyenne d'une variable quantitative.

      Prérequis. Échelles de mesure, Conventions de notation (en particulier, somme algébrique)

      Résumé. Soit une variable définie sur une population de N individus, on définit la moyenne de cette variable. On estime cette moyenne à l'aide de la moyenne d'un échantillon représentatif de la population.

      rédaction : Éric Raufaste
    • Produit cartésien Livre

      Objectifs. Introduire la notion d'ensemble 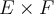E\times F, produit cartésien des ensembles E et F.

      Prérequis. Aucun.

      Utilisé comme prérequis dans les articles :

      Résumé. On note 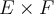E\times F, et on appelle produit cartésien "E croix F", l'ensemble de tous les couples formés d'un élément de l'ensemble E  et d'un élément de l'ensemble F .

      rédaction : Stéphane Vautier
    • Relation d'équivalence Livre

      Objectifs : définir le concept de relation d'équivalence, fondamental pour la classification des éléments d'un ensemble ; définir les concepts associés de partition et d'ensemble quotient.

      Prérequis : aucun.

      Utilisé comme prérequis dans les articles : Échelles de mesure

      Résumé : une relation d'équivalence \mathcal{R} est une relation binaire définie sur un ensemble E. \mathcal{R} est réflexive, symétrique et transitive. \mathcal{R} définit une partition de E. L'ensemble quotient E/\mathcal{R} est l'ensemble des parties de E induites par \mathcal{R}.

      rédaction : Stéphane Vautier
    • Relation d'ordre et ordre partiel Livre

      Objectifs : définir les notions de relation d'ordre et d'ordre partiel.

      Prérequis : Relation d'équivalence

      Utilisé comme prérequis dans les articles : Échelles de mesure

      Résumé : Soit une relation binaire \mathcal{R} définie sur un ensemble E. \mathcal{R} est une relation d'ordre si elle est (1) réflexive; (2) antisymétrique et (3) transitive ; \mathcal{R} est une relation d'ordre strict, si elle est (1) antiréflexive; (2) antisymétrique; et (3) transitive. Une relation d'ordre partiel, on dit aussi un ordre partiel, est une relation d'ordre telle qu'il existe certains couples (x, y) d'éléments distincts de E qui ne peuvent être comparés : tels que (x non\mathcal{R} y) et (y non\mathcal{R} x).

      rédaction : Stéphane Vautier
    • Somme algébrique Livre

      Objectifs. Rappeler la construction et la signification de l'opérateur de sommation discrète, utilisé dans de très nombreuses formules de statistique et psychométrie.

      Prérequis. Aucun.

      Résumé. La somme simple, d'abord présentée, est ensuite étendue à la somme double.

      rédaction : Éric Raufaste

◄Savoir Faire
►Références
Accessibilité
Tout remettre à zéro

Couleur de fond

Police

Taille de police

1

Couleur de texte