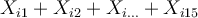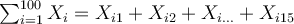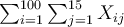Somme algébrique
Objectifs. Rappeler la construction et la signification de l'opérateur de sommation discrète, utilisé dans de très nombreuses formules de statistique et psychométrie.
Prérequis. Aucun.
Résumé. La somme simple, d'abord présentée, est ensuite étendue à la somme double.
rédaction : Éric Raufaste
2. La somme double
Imaginons que l'on ait à faire pour chaque sujet une somme des notes qu'il a obtenues à chacune de 15 épreuves. Puis que nous ayons besoin de calculer la somme des notes obtenues par l'ensemble des 100 sujets d'une expérience. Nous avons donc deux sommes emboîtées l'une dans l'autre.
Si nous considérons nos données, en indiçant chaque valeur par le numéro de sujet et le numéro de note pour le sujet 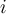 considéré, nous avons pour le sujet n°1 quelque chose comme
considéré, nous avons pour le sujet n°1 quelque chose comme
Pour le sujet n°2,
Jusqu'au sujet n°100 où cela devient complètement illisible,
Essayons donc de trouver une écriture plus lisible et plus dense. Afin d'obtenir une écriture un peu plus générale, nous pouvons variabiliser le numéro de sujet (i.e., le remplacer par une variable, disons ici une variable
i
qui variera de 1 à 100). Nous pouvons alors décrire une ligne de numéro
i
quelconque par la formule,
Puisque, à la page précédente, nous avons vu qu'il était possible de simplifier l'écriture avec l'opérateur de sommation, nous pouvons écrire  la somme sur les 100 sujets, soit
la somme sur les 100 sujets, soit
Cela reste assez lourd. Mais rien ne nous empêche de variabiliser aussi le numéro d'épreuve, par exemple en utilisant la variable
j, qui variera de 1 à 15 selon les 15 épreuves, puis d'appliquer une deuxième fois l'opérateur de sommation, à l'intérieur de chaque sujet. D'où la formule suivante, bien plus élégante puisqu'elle résume à elle seule toutes les opérations réalisées sur tous les sujets :
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte