Savoir trouver les valeurs critiques du t de student

Ayant procédé au test sous Statistica 8, notre chercheur obtient le tableau de résultats suivant :

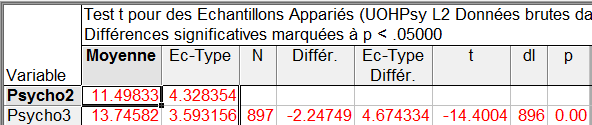
Explication des colonnes de données

La ligne 1 ne contient que les données descriptives de la variable Psycho2. La ligne 2 contient les données descriptives de la variable Psycho3 puis les données de statistique inférentielle. Les cellules en rouge correspondent aux tests significatifs, ce qui est le cas ici.

Moyenne : contient la moyenne des variables, ici 11.19833 pour Psycho 2 et 13,74582 pour Psycho3.

Ec-type : Il s'agit de l'écart-type des variables, ici 4.328354 pour Psycho 2 et 3,593156 pour Psycho3.

N : Il s'agit du nombre d'observations prises en compte, soit 897 observations pour lesquelles les deux variables sont renseignées.

Différ. : contient la moyenne des différences observées entre la variable 1 et la variable 2, ici -2.24749

Ec-type Différ. : Il s'agit de l'écart-type de l'échantillon constitué des différences entre Psycho2 et Psycho3 pour chaque sujet, soit 4,674334. 

t : C'est tout simplement la valeur du t de student arrondie à la 4^e décimale, soit t =-14.4004. Le signe négatif vient de ce que la différence (Psycho_2- Psycho₃) est négative.

dl : C'est le nombre de degrés de libertés de la comparaison, soit, pour une comparaison à échantillons indépendants, le nombre de sujets moins 1, soit 896.

p : C'est la valeur du risque de type 1 ou risque alpha, la fameuse valeur p. Ici, arrondie à la deuxième décimale, soit 0.00. Comme cette valeur est inférieure au de 5%, soit .05, on considérera le test comme significatif, et donc que l'épreuve 2 donne lieu à des notes significativement plus élevées que l'épreuve 3. Autrement, l'épreuve 3 semble plus difficile que l'épreuve 2. 

Comment rapporter les résultats

Classiquement, on rapportera la statistique descriptive dans une table ou dans le texte, et les statistiques inférentielles plutôt dans le texte.

Ici, nous imaginerons le cas de résultats rapportés dans un texte qui suit les normes APA 7^e édition.

Après avoir arrondi les valeurs, idéalement à la deuxième décimale, éventuellement à la troisième, cela pourrait donner quelque chose comme cela :

"La moyenne des résultats à l'épreuve Psycho2 est M₂ =11.50 (SD = 4.33) alors que celle des femmes est M₃ =13.75 (SD = 3.59). La moyenne des notes à Psycho3 est significativement plus forte t(896) = 14.4, p <.001".

En fait, on doit écrire p<.001 car, si l'on regarde la valeur du p calculé avec plus de décimales (ce qui n'apparaît pas sur l'image ci-dessus), on constate que la valeur de p est extrêmement proche de 0, et en tout cas inférieure à .001.