Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
1. Tester la liaison entre deux variables
1.1. Tester une corrélation simple
Le coefficient de corrélation linéaire, r , peut varier entre -1 et +1. Une valeur nulle indique l’absence de relation linéaire, soit parce qu’il n’y a pas de relation du tout entre les variables considérées (cas de l'indépendance entre les deux variables), soit parce que la relation existe mais n’est pas linéaire (par exemple la relation est une parabole).
Le coefficient de corrélation est un nombre sans dimension (il n’a pas d’unité, contrairement à une longueur ou un poids).
Pour tester si une corrélation est significativement différente de 0, on peut calculer une version particulière de la statistique t :
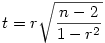
Cette statistique suit une loi de student à n -2 degrés de liberté. On peut donc la tester comme vu précédemment dans l'article sur le test du t .
Prenons un exemple numérique simple. Admettons que nous ayons calculé la corrélation entre deux variables mesurées sur un échantillon de 100 personnes et que nous ayons trouvé r =.305. Nous appliquons la formule et trouvons
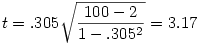
En accédant ensuite à la table du t ou bien à une formule de tableur équivalente, nous trouvons que pour (100-2)=98 degrés de liberté, la probabilité d'avoir un t au moins égal à 3,14 en valeur absolue est p =.002., donc notre r est significativement différent de 0, nous pouvons rejeter l'hypothèse nulle.
À noter : Statistica possède un petit outil qui calcule directement ces valeurs :
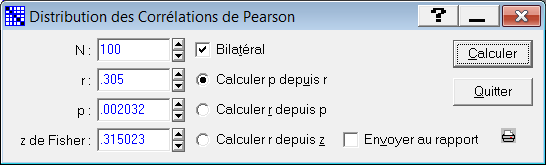
Notons que la corrélation est une variable signée dont la distribution est symétrique. Si nous avons une hypothèse sur le sens de la corrélation (donc le signe du r que nous devrions obtenir), et que la valeur observée de r est effectivement du signe attendu, nous pouvons calculer notre valeur p en unilatéral et donc diviser par deux le p obtenu par le test de Student. Ce qui ferait ici p =.001.