UOH / Statistique et Psychométrie en L2

Cette section est adaptée à partir d'un article de Steiger (1980) et en reprend les notations.

Il y a trois cas dans lesquels les corrélations à comparer ne sont pas indépendantes et où le traitement s'avère plus complexe :

• lorsque les corrélations ont été obtenues sur les mêmes sujets
• lorsque les corrélations partagent une variable en commun
• lorsque l'on teste la même corrélation à des moments différents

Nous ne traitons ici que du cas n°2 : Nous avons deux corrélations obtenues avec N sujets. Avec Steiger (1980), appelons j la variable commune, h et k les deux autres. Nos corrélations sont r_jk et r_jh .

1°) Il nous faut évaluer le degré de dépendance entre ces deux corrélations, et cette information nous est fournie par le calcul de la troisième corrélation, r_hk. À partir de ce moment, on dispose de trois corrélations.

2°) On applique la transformation de Fisher aux deux premières corrélations (rappelons que c’est la fonction arctangente hyperbolique), ce qui donne deux corrélations transformées r_jk' et r_jh' avec

   

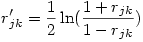
et 

    

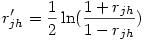
3°) Puisque nous testons l'hypothèse nulle que r_jk = r_jh, on peut avantageusement remplacer chacune des deux corrélations observées par la moyenne des deux et utiliser cette dernière dans les équations suivantes : 

      

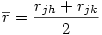
ou encore

     

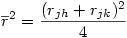
4°) On calcule ensuite

     

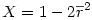
5°) On calcule alors un écart-type groupé S_hk

     

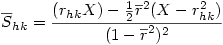
6°) Finalement la variable

  

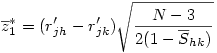
suit une loi normale classique qu'il suffit de tester comme toute valeur z.