Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
2. Régression linéaire simple : approche inférentielle
2.1. Analyses préalables
L’intérêt de ces analyses est surtout de repérer si les postulats de base de la régression linéaire sont remplis (comme la linéarité de la relation entre la VI et la VD) et si certaines valeurs ne se distinguent pas franchement du reste. Cela peut arriver notamment en cas d’erreur de saisie, ou encore un sujet peut n’avoir pas compris (ou pas voulu suivre) la consigne et produit des résultats tout à fait hors norme, et même parfois tout à fait incohérents.
À titre d'exemple, au cours de l'article, nous examinerons l’influence d’une variable nommée F02J sur une seconde variable nommée DVP. Pour l’exemple, peu importe ici ce que ces variables représentent.
1.1. Variables dépendante et indépendante
La première étape d'une régression consiste à entrer les variables à prendre en compte, en distinguant les variables dépendantes (variables prédites) et indépendantes (prédicteurs).
Il y a plusieurs variables indépendantes lorsqu’il y a plusieurs prédicteurs. Par exemple, on veut tester l’hypothèse que la réussite universitaire est prédite par une fonction linéaire (1) du nombre d’heures passées à travailler ET (2) du QI. On parle alors de « régression multiple ». Nous examinerons dans un autre article les problèmes qu’ajoute la régression multiple par rapport à la régression simple. Dans cette dernière, nous n'avons qu'une variable indépendante.
Simple ou multiple, la régression linéaire ne s’applique qu’à une seule variable prédite. Toutefois, il est possible dans certains logiciels de saisir plusieurs variables dépendantes. Celles-ci font alors chacune l’objet d’une analyse en régression indépendante des autres.
La régression simple consiste à produire l’équation d’une droite de la forme Y = aX + b, droite qui résume le mieux possible le nuage de points. D’une certaine manière, on peut dire que les valeurs de Y sont prédites par la combinaison d’une constante et d’une autre variable, X.
1.2. Analyse descriptive des variables considérées
On commence généralement par observer comment se présentent les variables qui vont entrer dans la régression.
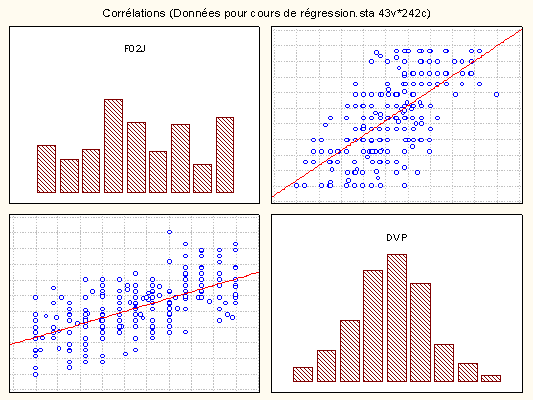
Ici, on voit que la variable à prédire (DVP) se distribue normalement alors que la variable prédictrice (F02J) est plutôt uniformément distribuée.
En dépit de ce qui se dit parfois, cela n'a aucune importance dans le cas de la régression : pour permettre l'inférence statistique, seuls les résidus de la régression doivent être normalement distribués pour que l'on puisse considérer que le modèle est satisfaisant !