UOH / Statistique et Psychométrie en L2

1.1. Pourquoi faire une corrélation partielle

Il arrive que l'on constate une relation positive entre deux variables, mais que cette relation paraisse curieuse. De fait, il arrive parfois qu'une corrélation soit illusoire : la relation existe statistiquement mais ne traduit pas un lien de cause à effet entre les deux variables. Pour illustrer cela, prenons un exemple caricatural mais parlant :

Supposons que l'on mesure la couleur des dents de participants de 50 ans, mesurée sur une échelle de 0 à 10, où 0 est blanc pur et 10 est noir pur. Supposons que l'on mesure par ailleurs l'espérance de vie en bonne santé de ces participants. Vingt ans après, on s'aperçoit que l'espérance de vie en bonne santé est beaucoup plus faible chez ceux qui ont les dents jaunes. L'espérance de vie ne peut pas causer les dents jaunes. Une analyse superficielle pourrait faire penser qu'avoir des dents sombres réduit l'espérance de vie. Cela paraît toutefois douteux, car on ne voit pas pourquoi la couleur des dents affecterait sensiblement la santé. Avec un peu de réflexion, on peut être amené à penser qu'une troisième variable cause à la fois le jaunissement des dents et une réduction d'espérance de vie en bonne santé. Et effectivement, une telle variable existe, à savoir le tabac qui d'une part jaunit les dents, et d'autre part provoque cancers, maladies cardiovasculaires, AVC, etc. La question du chercheur devient alors, "comment s'assurer que le tabac est bien le vecteur de la relation entre couleur des dents et réduction de l'espérance de vie en bonne santé ?". C'est ce que va lui permettre de tester la corrélation partielle.

1.2. Méthode de la corrélation partielle

Le principe de la corrélation partielle est de calculer une corrélation de la même façon que d'habitude, mais après avoir retiré de chacune des deux variables l'effet de la troisième variable, celle que l'on cherche à contrôler.

Pour retirer cet effet, nous allons utiliser une propriété essentielle de la régression linéaire : la régression permet de distinguer, pour chaque individu, une part de la note de la VD attribuable au facteur, et une part résiduelle, attribuable soit à des erreurs de mesure, soit à l'intervention d'autres facteurs, inconnus. Or justement ce résidu nous intéresse ici, car il représente la part de la VD qui n'est pas déterminée le facteur caché (linéairement en tout cas). 

Nous ne revenons pas ici sur le détail de la technique de régression. Il nous suffira de rappeler que lorsque l'on fait une régression, par exemple avec SPSS, Statistica ou un autre logiciel de statistiques, il est généralement possible d'enregistrer séparément les résidus et la partie prédite de chaque note : La partie prédite correspond à la part expliquée par le facteur et le résidu correspond à la part qui n'est pas expliquée par le facteur.

Techniquement, la régression permet de déterminer l'équation d'une droite de régression qui résume au mieux le nuage de points entre le facteur et la variable prédite. Cette droite est caractérisée par une équation 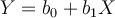$Y=b_0+b_1X$, où Y est la valeur de la VD et X la valeur de la VI (le prédicteur), b₀ et b₁ sont des constantes. Pour chaque sujet on a donc une valeur du prédicteur, et connaissant la valeur des paramètres, on peut calculer la valeur prédite correspondante. On note " Y chapeau" la valeur prédite de la VD :

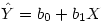
Dans la pratique, la valeur prédite est presque toujours différente de la valeur observée. On peut donc écrire que la valeur observée de la VD, Y, est égale à la valeur prédite plus un résidu :

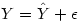
Nous avons vu dans le cours de L1 comment obtenir les coefficients b₀ et b₁. Donc, on peut calculer le résidu par différence des deux équations précédentes :

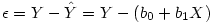
Si l'on calcule les résidus, sur Y et sur X, on obtient deux nouvelles variables dont aucune des deux ne dépend de Z, le facteur que l'on veut contrôler. On voit alors l'intérêt de passer par l'intermédiaire de la régression : pour obtenir la corrélation partielle qui retire l'effet du facteur que l'on suppose à l'origine de la corrélation, il suffit de calculer la corrélation entre les résidus de deux régressions, l'une où le facteur prédit la VD1, l'autre où le facteur prédit la VD2.