Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
3. Contrôler l'effet d'une variable : Corrélation partielle
3.2. Un exemple détaillé
2.1. Les données de l'exemple
Pour cet exemple, nous avons généré un jeu de pseudo données dans lesquelles deux "Variables dépendantes", VD1 et VD2, ont été créées par ajout d'une valeur aléatoire à chacune des valeurs d'une "Variable indépendante". Voici les données.
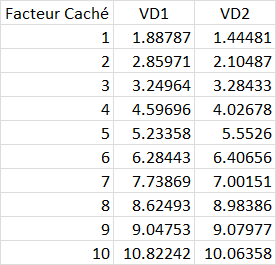
Par exemple pour le premier "sujet", le facteur caché est 1 et la VD 1 a été créée en ajoutant 0.88787 tandis que la VD2 était créée en ajoutant 0.44481.
2.2. La matrice de corrélations brutes
La matrice de corrélations que l'on obtient à partir de ces trois variables est la suivante :
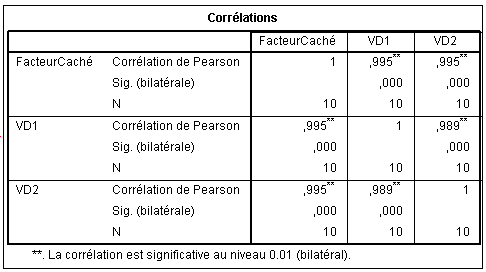
On voit que la relation entre la VD1 et la VD2 sont extrêmement fortes : .995 et très significatives évidemment malgré le petit effectif. Mais on voit aussi, et cela n'a rien d'étonnant, que le facteur caché est aussi très corrélé aux deux VD. Nous allons donc émettre l'hypothèse (vraie bien sûr puisqu'on a construit les données ainsi !) que le facteur caché explique en fait la corrélation entre VD1 et VD2. Mais comment nous en assurer ? Il faut faire une corrélation partielle.
Nous commençons par détailler le processus pour assurer la compréhension, mais toute cette opération est faisable en deux ou trois clics dans un logiciel comme SPSS.
Commençons par réaliser les deux régressions.
2.3. Les deux régressions simples
2.3.1. Régression de VD1 sur le facteur caché
Nous ne nous intéressons pas du tout ici à savoir si cette régression est significative car en réalité seul nous intéresse d'obtenir les valeurs des résidus.
Pour la compréhension, nous montrerons tout de même la reconstruction de l'équation de la droite de régression, donnés par le tableau des coefficients :
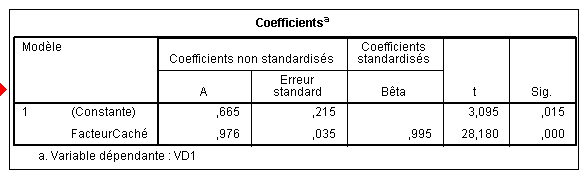
Nous obtenons ces coefficients dans la colonne A : b0 vaut .665 et b1, le coefficient attaché au facteur caché vaut .976. d'où l'équation
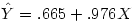
On peut enregistrer directement les prédictions et les résidus via une option de la régression et nous les obtenons directement dans les colonnes renommées ici Prévision1 et Résidu1:
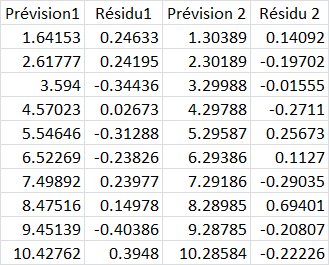
On peut facilement vérifier sur le sujet 1 que 1.64153+0.24633=1.88786 ce qui aux arrondis près correspond à notre VD observée 1.88787.
Et l'on vérifie aussi, toujours aux arrondis près (car la vraie valeur du coefficient b1 par exemple est 0.976231762090997), que la valeur prédite correspond à l'équation. En effet, la valeur du prédicteur étant 1 pour ce sujet, on a .665+1*.976=1.64153.
Le même raisonnement s'applique pour les coefficients, valeurs prédites et résiduelles de la régression 2 :
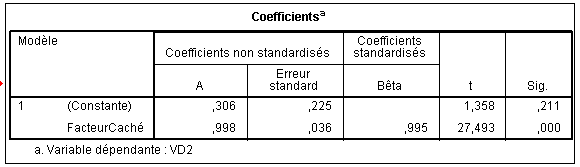
Ici, b0 vaut .306 et b1 , le coefficient attaché au facteur caché vaut .998. d'où l'équation
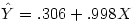
2.3. La corrélation partielle
Finalement, nous pouvons facilement calculer la corrélation entre les deux colonnes de résidus. Par exemple sous Excel avec la fonction "Pearson " et nous trouvons -.11013841. Il ne nous reste qu'à tester cette corrélation comme nous l'avons vu dans l'article sur le test des corrélations à un détail près : il y a ici n -3 degrés de libertés et non n -2 comme dans une corrélation normale. Nous trouvons alors p =.77788363.
En fait, SPSS nous permet de sortir directement la matrice où l'effet de la variable de contrôle, que nous avons nommée "FacteurCaché", sur la corrélation entre VD1 et VD2 est contrôlé :
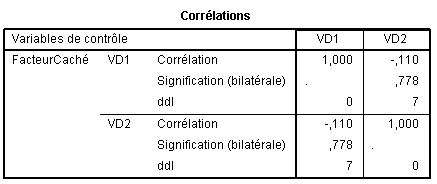
Ce qui correspond bien à nos calculs. Nous voyons à ce moment que la corrélation entre VD1 et VD2, une fois retiré l'effet du facteur caché s'effondre à -.110 et n'est plus du tout significative, comme on pouvait s'y attendre malgré la corrélation initiale apparemment extrêmement forte.