Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
6. Régression linéaire multiple : La redondance des VI
6.2. La multicolinéarité et son diagnostic
2.1. Définition de la multicolinéarité
La multicolinéarité est le fait qu’une VI est prédictible par (ou partage sa variance avec) une combinaison linéaire des autres VI. Pour faire simple, disons qu'une combinaison linéaire est une variable que l'on obtient en faisant la somme pondérée de plusieurs autres variables. Ainsi, si l'on crée une variable X3 en faisant la somme pondérée de deux autres variables X1 et X2, par exemple X3 = 2 X1 + 3 X2 , alors X1 , X2 et X3 seront multicolinéaires .
Du point de vue du diagnostic, la multicolinéarité se détecte en faisant la régression de l'une VI envisagée par les autres (on laisse provisoirement de côté la question de la VD). Le carré du R multiple obtenu dans cette régression représente la part de la variance de la VI expliquée par l'ensemble des autres VI. Cela représente donc en fait le degré auquel on peut dire qu'il existe une combinaison linéaire qui relie les VI. Idéalement, ce R² doit donc être minimal.
2.2. Définition de la tolérance
La tolérance est la part de la variance d'une VI qui n’est PAS expliquée par les autres VI. C'est donc le complémentaire à 1 du R² de la régression d'une VI par les autres VI (et qu’il ne faut surtout pas confondre avec le R² de la régression de la VD par les VI !!) :
Tolérance= 1- R².
Idéalement, elle doit être le plus élevé possible. Si la tolérance est plus petite que .10, cela mérite investigation. Si la tolérance est plus petite que .01, il n’est pas prudent (et en tout cas probablement peu intéressant) d’inclure la VI dans les analyses en plus des VI qui la prédisent.
Voici un exemple issu des diagnostics de redondance de Statistica :
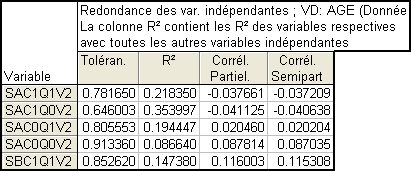
Voici un autre exemple issu de SPSS (avec l’option« tests de colinéarité » cochée) :
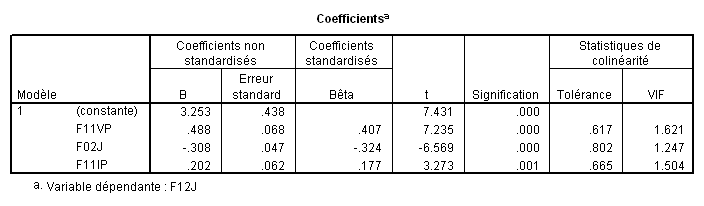
2.3. Facteur d'inflation de la variance
On remarque que SPSS donne aussi le « Facteur d'inflation de la variance » ou VIF (pour Variance Inflation Factor), qui est la valeur réciproque de la tolérance.
VIF= 1 / Tolérance
Des valeurs élevées de VIF indiquent donc la présence de multicolinéarité.
L’utilité diagnostique de cet indice résulte du fait que la variance du coefficient de régression augmente de la même façon que le facteur d'inflation de la variance. C’est pourquoi les tests de significativité des différents prédicteurs se trouvent améliorés par la suppression d’une VI qui induit de la multicolinéarité.