Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
7. Régression linéaire multiple : Ordre d'introduction des variables
7.8. Comparaison de deux ensembles de prédicteurs
Il s’agit de déterminer si un ensemble de VIsE1 prédit la VD mieux qu’un autre ensemble de VIs, E2.
Fondamentalement, il s’agit donc de comparer la corrélation multiple entre E 1 et la VD avec la corrélation multiple entre E 1 et la VD. On pourrait penser qu’il suffit de prendre les deux R multiples, et les introduire dans une banale comparaison de corrélations, comme nous appris à les faire ici). Le problème est que les corrélations à comparer ne sont pas indépendantes, comme l’assume le test que nous avons vu, mais partagent une variable commune, à savoir la VD.
Une solution est possible d’après Steiger(1980). La méthode est la suivante :
1°) On enregistre les scores prédits par chacune des deux modèles dans deux nouvelles variables.
2°) On calcule la corrélation entre ces deux variables.
À ce moment, on dispose de trois corrélations.
- Appelons ra la corrélation multiple entre la VD et l’ensemble de VIs E1 .
- Appelons rb la corrélation multiple entre la VD et l’ensemble de VIs E2 .
- Appelons rab la corrélation entre les prédictions des deux ensembles de VIs.
3°) on applique la transformation de Fisher à ces corrélations (rappelons que c’est la fonction arctangente hyperbolique, ce qui donne deux corrélations transformées ra' et rb' avec
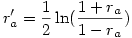
et
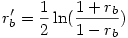
4°) On calcule ensuite
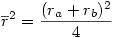
5°) puis
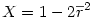
6°) On calcule alors
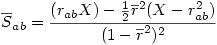
7°) Finalement la variable
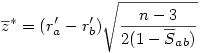
suit une loi normale classique.