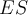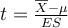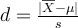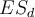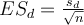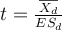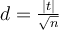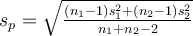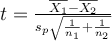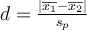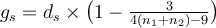t de student : un petit formulaire général: Formulaire Student

t de student : un petit formulaire général

Cette section présente un ensemble de formules permettant de réaliser manuellement des tests t de student.

test t à échantillon unique
test t à groupes appariés
test t à groupes indépendants

Pour chacun des types de test, une formule donne la taille d'effet sous forme du d de Cohen.

Formulaire Student

Avertissement : les formules présentées ici peuvent être sensiblement différentes en apparence à d'autres formules que vous pouvez trouver ailleurs. 
Toutes ces formules sont généralement mathématiquement équivalentes et produisent les mêmes résultats. 
Elles sont plus ou moins faciles à utiliser selon les informations dont vous disposez...

Le lecteur intéressé par les mathématiques de la chose pourra trouver une justification complète de tout cela dans l'excellent manuel
    Howell, D.C. (2008). Méthodes Statistiques en Sciences Humaines", 2e édition. De Boeck. 
(voir en particulier le chapitre sur le test d'hypothèses appliqué aux moyennes).

Démarche générale

On dispose d'hypothèses sur la comparaison des moyennes de deux populations, ou la comparaison de la moyenne d'une population et d'une valeur de référence;
On calcule une statistique t qui est le rapport d'un écart de moyennes (effet brut) par une erreur standard;
On détermine la valeur p d'avoir t(ddl) (où t est le t de student et ddl le nombre de degrés de liberté);
On prend une décision statistique sur la base de la valeur p;
On calcule la taille de l'effet (d de Cohen avec l'interprétation : 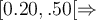$[0.20, .50[ \Rightarrow$ petit effet; 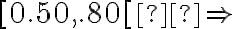$[0.50, .80[ \Rightarrow$ effet moyen ; 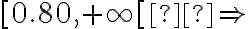$[0.80, +\infty[ \Rightarrow$ grand effet);
On présente les résultats (en utilisant des normes, le plus souvent en psychologie, les normes APA).

Cette démarche générale se décline selon diverses variantes au niveau des calculs de t, des ddl et de la taille d'effet.

A. Comparer la moyenne d'un échantillon et une constante de référence

Soit un échantillon de n mesures dont la moyenne est 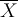$\overline{X}$ et l'écart-type s.
On veut comparer la moyenne 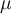$\mu$ de la population à une constante 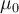$\mu_0$ de référence (généralement une valeur fondée théoriquement ou empiriquement).

l'effet brut est $\overline{X}-\mu$
On calcule l'erreur-standard de l'échantillon, $ES$ :

$ES=\frac{s}{\sqrt{n}}$

On a alors

$t=\frac{\overline{X}-\mu}{ES}$

où le nombre de degrés de liberté est simplement ddl= n-1

Ici la taille d'effet est le d de Cohen simple.

$d=\frac{|\overline{X}-\mu|}{s}$

B. Comparer les moyennes de deux échantillons appariés

Soit un ensemble de n paires de mesures. On calcule une nouvelle variable constituant, pour chaque paire, la différence des deux mesures précédentes. Sous l'hypothèse nulle, la moyenne théorique de ces différences est zéro. La nouvelle variable constitue un échantillon unique dont la moyenne est 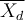$\overline{X_d}$ et l'écart-type 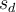$s_d$ . On se ramène donc au cas d'une comparaison de moyenne (la moyenne des différences) et la constante $\mu=0$ .

On calcule l'erreur-standard de l'échantillon des différences, $ES_d$ :

$ES_d=\frac{s_d}{\sqrt{n}}$

Il faut calculer la taille de l'effet, classiquement le d de Cohen. Ici, une formule simplifiée pour les groupes appariés le donne directement :

$d=\frac{|t|}{\sqrt{n}}$

On détermine la valeur p d'avoir t(ddl)
On utilise la valeur de p pour prendre une décision statistique
On présente les résultats inférentiels.

C. Comparer les moyennes de deux échantillons indépendants

Soient deux échantillons de mesures respectivement prises sur un groupe 1 de n₁ sujets, et un groupe 2 de n₂ sujets. Notons

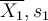$\overline{X_1}, s_1$ , et

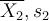$\overline{X_2}, s_2$ les moyennes et écarts-types de ces deux échantillons.

La structure est la même pour tous les tests t : il s'agit de faire le rapport d'une différence de moyennes par une erreur standard. Dans le cas des mesures indépendantes, le calcul de l'erreur standard commune aux deux échantillons est compliqué par le fait que les effectifs des deux groupes peuvent différer (i.e., 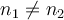$n_1\neq n_2$ ).

Les manuels distinguent souvent deux cas, selon que les effectifs sont équilibrés ou non, la relation se simplifiant dans le premier cas. Cela étant, la formule générale, quoique d'apparence un peu plus compliquée, marche dans tous les cas. À l'ère de l'informatique, nous ne voyons pas l'avantage d'enseigner deux formules aux étudiants de sciences humaines, au nom de la simplicité, quand la première suffit. Nous ne présentons donc ici que la formule générale.

On commence par calculer une sorte d'écart-type combiné (ou écart-type commun ou encore groupé) des deux groupes, souvent notée 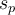$s_p$ dans les ouvrages ("p" pour "pooled" en anglais), et qui corrige notamment le problème des échantillons de tailles inégales (Howell, 2008, p. 200) :

$s_p=\sqrt{\frac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$

On obtient alors t par la formule :

$t=\frac{\overline{X_1}-\overline{X_2}}{s_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$

avec le nombre de degrés de liberté : 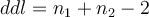$ddl=n_1+n_2-2$ .

Il faut encore calculer la taille de l'effet, qui pour les tests t est classiquement le d de Cohen (ou l'un de ses variantes). Dans le cas général, nous utiliserons la variante dite d standardisé (qui est en fait l'indice g de Hedges, aussi noté d_s par Cohen, ce dernier réservant la notation d à une formule simplifiée ne s'appliquant que pour des groupes d'égales variances et tailles) :

$d=\frac{|\overline{x_1}-\overline{x_2}|}{s_p}$

Pour les petits effectifs (<20), on applique une correction supplémentaire qui donne g_s ou "g de Hedges standardisé" :

$g_s = d_s\times\big(1- \frac{3}{4(n_1+n_2)-9}\big)$ .

Toutes ces variantes s'interprètent avec la même convention :

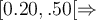$[0.20, .50[ \Rightarrow$ petit effet;

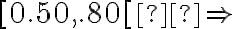$[0.50, .80[ \Rightarrow$ effet moyen ;

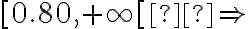$[0.80, +\infty[ \Rightarrow$ grand effet.

On détermine la probabilité p d'avoir t(ddl)
On utilise la valeur de p pour prendre une décision statistique
On présente les résultats inférentiels.

Note concernant les tailles d'effet

Trois remarques s'imposent.

La plupart des logiciels donnent des formules où d est signé. En fait, on ne s'intéresse pas vraiment au signe du d, puisqu'il ne dépend que de spécificités opérationnelles susceptibles de rendre les valeurs incomparables d'une étude à l'autre, alors que le but du calcul de taille d'effet est précisément de s'affranchir de ces spécificités non pertinentes. De plus, les conventions usuelles d'interprétation font généralement référence à la valeur de d en valeur absolue. Nous donnons donc ici les formules en valeur absolue, et si vous voyez le d signé dans un logiciel, ne tenez compte que de la valeur absolue.
Versions corrigées du d : Le d de Cohen est légèrement biaisé surtout en cas de petits échantillons (si < 20). On utilise donc généralement à sa place (le plus souvent sans le dire) la variante du g de Hedges qui utilise l'écart-type combiné. Pour les petits échantillons, on utilise en plus le g de Hedges corrigé. Enfin, pour le test de student à échantillons indépendants, on utilise de plus en plus une variante du t de student, le test de Welch, qui requiert aussi une altération du calcul de d. Nous donnons donc ici les formules pour les trois indices. Si le calcul de ces indices est différent, leur interprétation suit les mêmes conventions.
Certains textes (dont les normes APA 6^e édition, mais c'est corrigé dans la 7^e édition) indiquent à tort qu'il n'est pas nécessaire de rapporter la taille d'effet si les résultats ne sont pas significatifs. C'est un non-sens au regard de l'idée même de taille d'effet, qui sert à établir des méta-analyses ou évaluer la puissance statistique (notamment les effectifs) nécessaire pour atteindre un résultat significatif : rapportez TOUJOURS les tailles d'effet.

UOH / Statistique et Psychométrie en L2