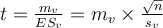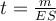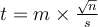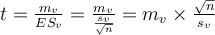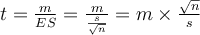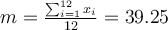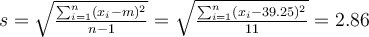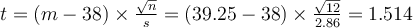Statistique : comparer des moyennes
| Site: | IRIS - Les cours en ligne de l'UT2J |
| Cours: | UOH / Statistique et Psychométrie en L2 |
| Livre: | Statistique : comparer des moyennes |
| Imprimé par: | Visiteur anonyme |
| Date: | jeudi 29 janvier 2026, 20:01 |
Description
 Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
Cette grande leçon introduit les principales stratégies permettant de comparer des moyennes par rapport à une valeur de référence ou des moyennes entre elles.
Le test de student est étudié en détail, ainsi que l'ANOVA à un facteur. On introduit les concepts de comparaisons planifiées et tests-post-hoc.
Table des matières
- 1. Principe général de la comparaison de moyennes
- 2. Comparer deux moyennes : test du t de Student
- 3. Comparer plus de deux moyennes : L'ANOVA à un facteur
- 3.1. Table d’orientation pour l'ANOVA À 1 FACTEUR
- 3.2. Philosophie de l'ANOVA à un facteur
- 3.3. Variations et variance dans l'ANOVA
- 3.4. Somme des carrés et carré moyen
- 3.5. Décomposer la somme des carrés
- 3.6. Calculer la somme des carrés totale
- 3.7. Calculer la somme des carrés inter-groupes (SC du facteur)
- 3.8. Calculer la somme des carrés intra-groupes
- 3.9. ANOVA et calcul des valeurs-p
- 3.10. Comment présenter les résultats d'un test d'ANOVA ?
- 4. Introduction aux comparaisons planifiées dans une ANOVA
- 5. Comparaisons planifiées dans l'ANOVA : contrastes
- 6. Comparaisons non planifiées : tests post-hoc
- 7. Questionnaire d'auto-évaluation
1. Principe général de la comparaison de moyennes
Objectifs. Mettre l'étudiant en position de comprendre quand et pourquoi réaliser une comparaison de moyennes à un ou plusieurs groupes. L'aiguiller vers les essentiels qui expliquent comment le faire concrètement.
Prérequis.
Voir aussi : Vidéos de savoir-faire sur la comparaison de moyennes
Résumé. On commence par introduire la notion de comparaison de moyennes sur un exemple. On montre que l'utilisation de la moyenne permet de gommer partiellement les effets aléatoires. Néanmoins, on ne peut éviter de recourir à la démarche générale de l'inférence statistique. On montre alors comment cette démarche s'applique dans différents cas de comparaisons de moyennes (de 1 à n groupes) en spécifiant notamment la construction de l'hypothèse nulle.
Le détail de la technique des différentes pratiques est présenté dans la rubrique des savoir-faire, et en particulier les vidéos de démontration des techniques paramétriques de comparaisons de groupes (t de student et sur l'ANOVA) ainsi qu'aux vidéos sur les techniques non paramétriques de comparaison de groupes.
1.1. Introduction à la comparaison de moyennes
A. Un exemple : évaluer l'effet d'une méthode thérapeutique

Commençons par un exemple simple : vous disposez d'une nouvelle technique psychothérapeutique dont vous voulez tester l'effet sur le bien-être des sujets qui la reçoivent. Vous projetez donc de mesurer par exemple l'humeur des patients avant et après la thérapie. Si la moyenne a augmenté, c'est que la thérapie (ou une autre cause que vous ignorez) a amélioré le bien-être des patients, dans les autres cas, l'intérêt de mettre en œuvre une telle thérapie serait douteux.
Passant à l'action, vous préparez une série de mesures sur un certain nombre de patients dont vous évaluerez l'humeur générale avant qu'ils commencent la thérapie. Idéalement, vous devriez aussi mesurer l'humeur chez un certain nombre de patients qui ne recevront pas la thérapie, ce qu'en méthodologie expérimentale on appelle un "groupe contrôle", mais laissons ce problème de côté pour le moment.
Certains sujets ont l'air contents d'avoir reçu la thérapie, d'autres sont moins convaincus. Il est donc très possible que d'autres facteurs que la thérapie aient joué un rôle dans l'humeur de certains patients, que ceux-ci en soient conscients ou non (facteurs de santé, interaction entre le patient et le thérapeute, disparition d'une cause environnementale de stress, autres facteurs non identifiés). En d'autres termes, il se peut que vous observiez une amélioration, mais que celle-ci ne soit que le fait du hasard, c'est-à-dire la façon dont les sujets auront été, au moment de la mesure, confrontés à toutes sortes de petits effets qui font varier l'humeur et que vous ne contrôlez pas (le degré de fatigue, une rencontre amoureuse, un petit événement anodin plaisant pour la personne, etc.) Dans ces conditions, comment savoir si les éventuels changements de l'humeur générale que vous aurez mesurés sont imputables ou non à la thérapie ou à l'effet aléatoire d'une multitude de facteurs que vous ne maîtrisez pas ?
Ou pour le dire plus techniquement, vous avez deux échantillons de mesures, avant et après, et vous avez besoin de savoir si l'écart entre les deux échantillons est suffisamment grand et stable pour que vous puissiez considérer que la thérapie a un effet positif. Comment faire ?
1.2. Une propriété intéressante de la moyenne : gommer les aléas.
...et ce d'autant plus qu'on la calcule sur un grand nombre d'observations.
Admettons, pour simplifier, qu'il existerait une "vraie" valeur d'humeur pour chaque individu, valeur que vous cherchez à mesurer et à améliorer par une thérapie. Mais les individus vivent des expériences diverses qui constituent autant de perturbations de l'humeur. Chacune de ces perturbations est comme un petit effet aléatoire qui va dévier la mesure de l'humeur. Par exemple, Lucas aura appris la veille une mauvaise nouvelle, et son score individuel s'en trouvera abaissé indépendamment de la thérapie. Par ricochet, le score moyen de son groupe se trouvera aussi abaissé.
Par définition, les petits effets aléatoires sont imprévisibles. De ce fait, si beaucoup de petits effets se cumulent, certains vont tirer la moyenne vers le haut, d'autres vers le bas. Ils vont donc tendre à s'annuler les uns les autres et on peut montrer qu'en augmentant le nombre de sujets, les moyennes des échantillons obtenus tendent vers la "vraie" moyenne (sauf bien sûr s'il existe un biais systématique dans le recueil) : Plus vos échantillons de mesures avant et après seront importants, et moins vous risquerez de faire d'erreur en vous servant de ces échantillons comme étant des valeurs proches de la vraie valeur.
Pour le dire plus techniquement, et toutes choses étant égales par ailleurs,
_ plus l'échantillon de mesures avant est grand, et plus la moyenne de l'échantillon des mesures avant sera proche de la "vraie" valeur d'humeur des sujets n'ayant pas reçu la thérapie.
_ plus l'échantillon de mesures après est grand, et plus la moyenne de l'échantillon des mesures après sera proche de la vraie valeur d'humeur des sujets ayant reçu la thérapie.
De ce fait, en comparant les deux valeurs, vous obtiendrez une estimation de l'efficacité de la thérapie.
Mais d'abord examinons de plus près ce que signifie vraiment "comparer des moyennes".
1.3. Que signifie comparer des moyennes ?
Comme il a été vu dans le cours de statistiques descriptives consacré à la moyenne, celle-ci est un indice de tendance centrale. Autrement dit, une moyenne représente fondamentalement le centre d'un ensemble de points, on dit souvent d'un "nuage" de points. La comparaison de moyennes peut donc se concevoir comme l'évaluation de la distance entre le centre d'un nuage de points (le "point moyen" de ce nuage) et une autre valeur prise en référence. Cette autre valeur peut être la moyenne d'un autre groupe, comme lorsque nous comparons les moyennes des tailles des individus d'un groupe d'hommes et d'un groupe de femmes. Ce peut aussi être une constante. Ainsi je peux vouloir prendre un groupe d'individus donnés, disons des enfants ayant été victime de la famine, et tester s'ils ont en tant que groupe un QI plus petit, plus grand, ou égale à la moyenne de la population globale. Celle-ci étant par construction égale à 100, je vais donc comparer le centre du nuage de points constitué par les mesures prises sur le groupe que j'étudie et rapporter cette valeur calculée à la valeur de référence de la population générale, 100.
Rappelons au passage que cette valeur calculée peut n'avoir aucune existence réelle. Ainsi, lorsque l'on calcule que le français moyen a 1,9 enfants, il est bien clair qu'il n'existe aucun français réel ayant véritablement 1,9 enfants !
Revenons à votre problème de départ, évaluer l'effet d'une thérapie. Arrivé là, vous disposez d'une stratégie pour avoir des estimations relativement fiables, pourvu que vous disposiez de suffisamment de participants pour vos mesures... Mais, avez-vous complètement résolu votre problème ?
En fait non. Tout d'abord, les participants ne sont pas en nombre infini. Ainsi, vos estimations ne fourniront jamais la vraie valeur, mais resteront toujours de simples estimations entachées d'un certain risque d'erreur. Dans la pratique, vous serez même généralement obligés de vous contenter d'un nombre très limité d'observations et donc non seulement vous n'aurez que des estimations, mais encore, il n'est pas sûr du tout que ces estimations soient bonnes !
Voilà qui nous amène au deuxième problème technique à résoudre : comment tenir compte du caractère nécessairement imparfait de vos échantillons ? C'est précisément là que la question de l'inférence statistique entre en jeu.
1.4. L'inférence statistique dans la comparaison de moyennes
Comme il a été évoqué dans les articles sur l'inférence statistique, cette dernière consiste généralement dans un premier temps à poser tout d'abord une hypothèse dite nulle, selon laquelle la totalité des effets observés seraient dus au pur hasard (compte tenu de la structure de la situation bien sûr). On prend ensuite une décision qui met en balance deux risques opposés : le risque de se tromper si l'on fait comme si l'hypothèse nulle était vraie (c'est-à-dire qu'on décide d'attribuer, à tort, toutes les variations observées, au seul effet du hasard) et le risque de se tromper en considérant que l'hypothèse nulle était fausse (c'est-à-dire que l'on décide de considérer que quelque chose de systématique était à l'œuvre alors qu'en fait seul le hasard a joué un rôle dans les résultats).
Pour prendre cette décision, on s'appuie sur des techniques statistiques, qui varient selon les situations, et qui permettent de calculer la probabilité que les données que l'on a réellement observées soient compatibles avec cette hypothèse nulle. Ou pour le dire plus simplement, on calcule la probabilité que les données obtenues soient le fruit du hasard. Cette probabilité est alors rapportée à une valeur conventionnelle d'acceptabilité, typiquement 5% dans la recherche scientifique. Bien entendu, si le risque associé à un certain type d'erreur est exceptionnellement grand, on pourra se donner des seuils de décision plus sévères ou plus laxistes, selon les cas.
Ceci posé, examinons comment cette stratégie s'applique dans le cas de la comparaison de moyennes.
4.1. L'hypothèse nulle dans la comparaison de moyennes
Dans le cas de la comparaison de deux moyennes d'échantillons, il y a bien sûr toujours une différence entre les deux moyennes, il suffit pour cela de se donner la précision de mesure suffisante. L'hypothèse nulle, on ne le répétera jamais assez, est l'hypothèse selon laquelle seul le hasard explique les variations de mesures. Donc, dans le cas de la comparaison des moyennes de deux groupes, l'hypothèse nulle consiste à considérer que les différences de moyennes entre les deux groupes sont dues au hasard. Et par conséquent, que la "vraie" valeur moyenne de chacune des populations d'où sont tirés les échantillons est en fait unique1.
Cette analyse se généralise sans difficulté au cas de plus de deux groupes. Si nous avons par exemple 10 groupes, l'hypothèse nulle énonce que les valeurs "vraies" des populations dont sont issus les 10 groupes sont identiques.
Dans le cas d'un seul groupe comparé à une constante, l'hypothèse nulle revient à dire que la moyenne observée de l'échantillon ne s'écarte de la constante de référence que par l'effet du hasard, et donc que la valeur vraie de la population d'où est tiré l'échantillon est exactement la valeur de référence.
1. Une précaution intellectuelle : attention au fait que même si les populations ont la même valeur "vraie", cela ne signifie pas forcément pour autant qu'il n'y a qu'une seule et même population sous-jacente aux différents échantillons. Ces populations peuvent diverger sur d'autres critères qui n'ont pas été mesurés.
4.2. Le calcul de la valeur-p
Nous distinguerons ici essentiellement deux techniques pour calculer cette probabilité dans le cas de la comparaison de moyennes : le test du t de Student et l'analyse de variance ou ANOVA.
L'étude de ces deux techniques requiert des articles complets pour chacune d'elles, aussi nous bornerons-nous ici à dire que ces techniques sont en réalité complémentaires et que la règle de décision suivante s'applique pour choisir quelle technique utiliser :
- Si vous avez seulement un groupe (à comparer à une constante de référence) ou deux groupes (indépendants ou appariés), alors il vaut mieux utiliser le test de t. En particulier, si vous avez des hypothèses orientées (non seulement vous attendez des différences, mais encore vous avez une théorie permettant de prévoir quel groupe aura la moyenne la plus élevée, ou bien votre théorie vous permet de prédire dans quelle direction la valeur moyenne s'écartera de la valeur constante de référence), alors le test t sera plus facilement significatif que l'ANOVA.
- Si vous n'avez que deux groupes et pas d'hypothèse orientée, les deux techniques sont équivalentes.
- Si vous avez plus de deux groupes, seule l'ANOVA s'applique.
2. Comparer deux moyennes : test du t de Student
Objectifs. Mettre l'étudiant en position de savoir quand et comment réaliser une comparaison de moyenne(s) à un ou deux groupes.
Prérequis.
- Cours de L1
- Approche intuitive de l'inférence statistique
- Hypothèse nulle
- Principe général de la comparaison de moyennes.
Résumé. On expose la technique générale des trois principaux cas de test t :
- comparaison d'un échantillon à une constante ;
- comparaisons de deux échantillons indépendants ;
- comparaison de deux échantillons appariés.
Le cas du test t dans les analyses post-hoc est renvoyé à l'article sur l'ANOVA.
2.1. Comprendre le test de Student
A. Dans quel cas appliquer un tel test ?

Objectif. Le test du t de Student s'applique lorsque l'objectif est soit de comparer deux moyennes entre elles, soit de comparer une moyenne contre une constante.
Type des informations disponibles : Les valeurs mesurées doivent être numériques, faute de quoi l'idée même de moyenne n'a pas de sens.
Distribution des observations : Les données doivent être normalement distribuées : l'histogramme doit être symétrique et ressembler peu ou prou à une courbe en cloche. On peut aussi appliquer des tests formels de normalité.
Condition d'indépendance : Les données doivent être indépendantes (les données d'un sujet ne sont pas censées avoir influencé les mesures faites sur un autre sujet).
B. Qu'est-ce que la statistique t ?
B.1 Rappel sur la loi normale centrée réduite
Vous trouverez dans le cours de L1 une présentation simple de la loi normale centrée réduite, accompagnée d'un générateur de simulations pour que vous puissiez faire des tests : Cliquez ici pour y accéder.
B.2 Notions d'échantillons virtuels et réels.
Avertissement : Ces deux notions sont propres au présent cours et vous ne les trouverez sans doute nulle part ailleurs. Nous les introduisons afin de permettre une vue générale du test t.
Nous appelons ici échantillon réel un ensemble de mesures directement réalisées sur une population. Par exemple, une mesure d'intelligence prise sur un ensemble de participants à une étude.
Nous appelons échantillon virtuel l'échantillon des données composé à partir des éléments à comparer. Ces éléments peuvent être (1) un échantillon réel et une constante (cas de la comparaison d'une moyenne à une constante); (2) deux échantillons réels de mesures indépendantes (c.-à.d. des mesures prises sur des individus différents et qui ne se sont pas influencés par ailleurs); (3) deux échantillons réels de mesures appariées (c.-à.d. des paires de mesures prises pour chaque individu, où la première mesure va dans l'échantillon réel 1 tandis que la seconde mesure va dans l'échantillon réel 2).
B.3 Formule générale de la statistique
t.
Dans toutes les formes du test de Student, la statistique calculée se nomme " t ". Soient mv la moyenne d'un échantillon virtuel de taille nv et ES v son erreur-standard (on rappelle que l'erreur standard d'un échantillon s'obtient en divisant l'écart-type par la racine carrée de l'effectif), on a
Cette formule s'applique dans le cas des trois tests t considérés dans cet article, test t pour échantillon unique, pour échantillons appariés et pour échantillons indépendants. Comment est-ce possible ? Tout simplement parce que l'échantillon auquel nous faisons référence ici est un échantillon virtuel que nous construirons différemment dans les trois cas. Nous verrons comment plus loin mais, pour l'instant, continuons l'analyse sur cet échantillon virtuel.
Pourquoi utiliser cette note t plutôt que simplement une valeur centrée-réduite z dont la distribution est connue puisque c'est celle de la loi normale centrée-réduite ? Eh bien, pour la raison suivante, qui se comprend par un raisonnement en deux points.
- Parce que si la moyenne mv et l'écart-type sv de l'échantillon peuvent être considérés comme des estimateurs des paramètres "réels" de la population d'où est tiré l'échantillon, à savoir sa moyenne μ et son écart-type σ, ces estimateurs ne sont pas l'exacte réalité mais seulement une approximation de la réalité.
- Si cette approximation de la moyenne μ par m peut être considérée comme fiable (au sens où si l'on tirait un nombre infini d'échantillons, la moyenne des moyennes issues de tous ces tirages convergerait vers la "vraie" moyenne, celle de la population), ce n'est pas le cas pour l'écart-type s . En effet, ce dernier est biaisé de façon systématique par rapport à l'écart-type σ de la population d'où est extrait l'échantillon, et la taille du biais dépend de la taille des échantillons que l'on prend : plus l'échantillon est petit et plus le biais est important. Il nous faut donc une loi qui corrige ce biais. Comme ce biais dépend de la taille des échantillons, il faut que cette loi admette un paramètre qui représente cette taille alors que la loi normale centrée-réduite ne dépend pas du tout de l'effectif.
Mais alors, si l'on ne peut pas utiliser la loi normale...
C. Comment obtenir la valeur p associée ?
C.1. La loi du
t
La variable t suit elle-même une loi ou distribution, dite loi du t de Student que l'on a présentée dans le cours de première année. Simplement, on peut considérer que les valeurs de t constituent une loi normale aménagée pour corriger le biais induit par la petite taille de l'échantillon. Plus l'échantillon est grand et moins il y a de biais à corriger et donc plus la loi du t ressemble à la loi normale.
La loi normale dépend de la moyenne et de l'écart-type, mais dans la loi centrée-réduite, ces deux paramètres sont fixés à 0 et 1 de sorte que la loi normale centrée-réduite est entièrement déterminée. La loi du t en est une sorte d'adaptation. Elle dépend d'un paramètre supplémentaire, le nombre de degrés de liberté, qui traduit l'ampleur de la correction qu'il faut apporter. Si l'on connaît le nombre de degrés de liberté, on peut alors déduire les valeurs p associées exactement selon les mêmes principes que l'on a utilisés pour la loi normale centrée réduite.
Il existe des tables du t que l'on peut utiliser lorsque l'on n'a pas de logiciel, mais on trouve maintenant des logiciels gratuits, à commencer par le tableau de la suite OpenOffice, permettant de calculer les valeurs de p associées à t avec précision. Vous trouverez ici des vidéos de démonstration du calcul du test de student.
C.2. Unilatéral ou bilatéral ?
Comme la distribution du z, la distribution du t est symétrique autour de 0. Par conséquent, si l'on possède une hypothèse théorique précisant le sens de la différence attendue des moyennes que l'on compare (par exemple, on s'attend à ce que la taille moyenne des garçons soit supérieure à la taille moyenne des filles d'une même classe d'âge) ET que les résultats vont dans le sens attendu, alors on peut diviser la valeur p que donnait le test bilatéral par deux. Ainsi, pour 50 degrés de liberté une valeur de t =1.69 est associée à une valeur p de 0.0972. C'est supérieur au seuil conventionnel de 5% et donc on dira que ce n'est pas significatif (on pourra cependant parler de "tendance" car la valeur p est comprise entre .05 et .10.
Si l'on peut travailler en unilatéral, on divise cette valeur par 2, ce qui donne p =.049, ce qui cette fois est significatif. Bien évidemment, lorsque vous rapportez vos résultats, il faut préciser que la valeur a été calculée en unilatéral.
D. Comment présenter les résultats d'un test t ?
Nous nous basons ici sur les normes internationales en vigueur en psychologie, les normes de l'APA (American Psychological Association), 7e édition.
D.1. Les statistiques descriptives
Le test du t est avant tout une comparaison de moyennes, comparaison qui repose sur une ou des mesures de dispersion. Il faut donc impérativement rapporter les données de statistiques descriptives, y compris la dispersion. Les débutants ont souvent tendance à l'oublier, tout à la joie de pouvoir rapporter un résultat "significatif", mais les statistiques inférentielles ne sont que des informations de second ordre, des indicateurs sur la fiabilité des résultats obtenus. Les informations de premier ordre, celles qui disent ce que l'on a vraiment observé, ce sont les statistiques descriptives et non les statistiques inférentielles !
Ces statistiques descriptives peuvent être présentées dans le texte du compte-rendu ou bien, le plus souvent, dans une table.
Lorsque l'on compare des groupes de tailles différentes, il est courant de donner comme indice de dispersion non pas la variance ou l'écart-type, qui sont très sensibles à la taille de l'échantillon, mais l'erreur standard qui l'est moins. On l'a dit plus haut, l'erreur standard s'obtient en divisant l'écart-type par la racine carrée de la taille de l'échantillon. Par exemple, si l'écart-type vaut 3.0 et qu'il y a 20 sujets, cela fait une erreur standard de 3/racine(20) = 0.67.
D.2. Les statistiques inférentielles.
Comme la distribution du t dépend du nombre de degrés de liberté, il convient de préciser celui-ci lorsque vous rapportez vos résultats. Cela donne une structure de la forme suivante :
t (ddl)=n.nn, p =.xxx
- ddl est le nombre de degrés de liberté. Dans un test t, c'est le nombre de sujets de l'échantillon virtuel diminué de 1. Nous verrons dans chacun des trois cas de test t comment calculer ce nombre.
- La valeur n.nn peut se rapporter avec un signe ou non mais, en tout cas, il est inutile de rapporter plus de deux décimales. Les logiciels donnent souvent des valeurs signées et avec plus de deux décimales, mais en pratique le signe du t est sans importance, et donner plus de deux décimales est foncièrement inutile.
Enfin, la façon de rapporter les valeurs de p est tout à fait conventionnelle et ne dépend pas du type de test utilisé 1 .
1. Selon les normes de publication en vigueur en psychologie scientifique, il est maintenant d'usage de rapporter, outre les valeurs de t et le p associé, une variable représentant ce qu'on appelle la "taille d'effet". Le calcul manuel de cette dernière n'est pas encore intégré dans la présente version de ce cours. Le calcul par logiciel des tailles d'effets est toutefois présenté dans les vidéos de savoir-faire sur les comparaisons de moyennes.
2.2. Comparer un échantillon contre une constante

- 1. Il faut soit avoir un échantillon de données recueillies à raison d'une seule valeur par sujet, soit deux échantillons d'un même type de mesures (par exemple, un temps de réponse dans les deux cas) recueillis à raison de deux données par sujet et sur lesquelles on peut procéder à une différence, laquelle sera comparée à une constante, généralement 0, mais pas nécessairement.
- 2. Les données de l'échantillon devraient idéalement être normalement distribuées. Cliquez ici pour accéder à l'article expliquant comment vérifier si cette condition est réalisée.
- 3. Il faut disposer d'une hypothèse sur une valeur de référence. Par exemple, si l'on connaît la valeur moyenne de la variable mesurée dans la population de référence, comparer l'échantillon à cette valeur de référence permet de tester s'il est raisonnable de considérer que notre échantillon provient bien de la population de référence.
- 4. L'hypothèse nulle est ici la suivante : m = c. Ou encore, ce qui revient au même m - c = 0. Par exemple, si l'on veut tester une hypothèse selon laquelle l'intelligence générale augmente de génération en génération depuis qu'on la mesure (ce qu'on appelle "l'Effet Flynn"). Supposons qu'on dispose d'un test utilisé il y a trente ans. On sait qu'à l'époque une performance donnée sur le test correspondait à l'époque à la valeur de QI=100. On fait passer le test à des jeunes actuels. On observe donc une nouvelle moyenne. On va alors comparer cette moyenne à la valeur de référence 100. Et si l'on trouve que le QI actuel est significativement supérieur à 100 tel que mesuré sur cet outil utilisé à l'époque, alors on pourra conclure que le QI a monté.
Voir aussi : vidéo de savoir-faire sur le test de student à échantillon unique par logiciels
Préalables spécifiques de cette version du test de Student :
2.1. Obtenir la valeur de
t
2.1.1. Pour les pressés : "En très bref"
Soit notre échantillon réel de taille n, de moyenne m et d'écart-type s, et soit c la constante à laquelle on veut le comparer.
Selon les informations dont on dispose, on applique la formule avec l'erreur standard ES,
ou, ce qui revient au même, celle avec l'effectif et l'écart-type d'échantillon,
On présente le résultat en écrivant t(ddl)=n.nn (pour la présentation de la valeur p, voir l'article général sur la norme APA de présentation du t).
Voir aussi le lien de pratique avec les logiciels de statistiques :
_
Interpréter des résultats de test t à échantillon unique
2.1.2. Pour ceux qui aiment comprendre : D'où cela vient-il ?
Dans le test du t de Student, la statistique calculée est précisément la valeur t. Dans le cas de la comparaison d'un échantillon contre une constante, voyons quelle formule employer. Commençons par rappeler la formule générale du t :
Soient mv la moyenne d'un échantillon virtuel de taille nv et ES v son erreur-standard, on a
Ici notre échantillon virtuel a pour moyenne
mv
=
(m
-
c)
où m
est la moyenne de l'échantillon réel et
c
la constante à comparer. Et on a aussi
ESv
=
ES, où ES est l'erreur standard de l'échantillon réel.
Démonstration. Ce dernier point résulte des propriétés générales de la variance : si l'on construit une nouvelle variable en faisant pour chaque sujet la différence entre la variable de départ et une constante, la variance de la variable d'arrivée est la même que la variance de la variable de départ. Ce qui se comprend aisément puisque la variance étant la dispersion de la variable, la nouvelle variable est tout aussi dispersée que la première ! Les échantillons virtuels et réels ont aussi, dans ce cas, la même taille. Puisque la formule de l'erreur-standard ne dépend que de la variance et de l'effectif, les deux erreurs-standard sont donc égales. CQFD.
Application : De ce qui précède, il suit que
2.2. Comment obtenir la valeur p associée ?
Il nous faut connaître la valeur t bien sûr et le nombre de degrés de libertés.
Ici l'échantillon virtuel a la même taille que l'échantillon réel, soit n individus. Le nombre de degrés de libertés est directement ddl=n -1.
Si elle n'est pas directement donnée par votre logiciel de statistique, la valeur p associée s'obtient
- soit en regardant dans une table du t de student en prenant comme entrée la valeur du t ainsi calculée et comme nombre de degrés de libertés la valeur n -1 où n est le nombre de mesures.
-
Soit au moyen d'une formule de tableur sous Microsoft Office Excel ou OpenOffice Calc : "=LOI.STUDENT.BILATERALE(
t
;
ddl
)"
2.3. Unilatéral ou bilatéral ?
Par défaut, on travaillera en bilatéral et on se contentera de la valeur p précédemment obtenue.
Si toutefois on dispose d'une hypothèse orientée et que les statistiques descriptives vont dans le sens attendu (typiquement, on s'attend à ce que m > c et c'est le cas au niveau descriptif, ou bien, on s'attend à ce que m < c et c'est le cas au niveau descriptif), alors on peut travailler en unilatéral : Il suffit alors de prendre la valeur p précédemment obtenue et la diviser par deux avant de décider si le test est significatif ou non.
2.4. Un exemple
Supposons que l'on ait une hypothèse théorique selon laquelle les astronautes en général (qu'ils aient ou non marché sur la lune) devraient avoir plus de 38 ans en moyenne.
Imaginons que la seule information dont nous disposions est l'âge des astronautes qui ont marché sur la lune au moment de leur sortie sur notre satellite. Nous obtenons le tableau suivant :
| Individu | Age |
| 1 | 38 |
| 2 | 39 |
| 3 | 39 |
| 4 | 37 |
| 5 | 47 |
| 6 | 39 |
| 7 | 39 |
| 8 | 41 |
| 9 | 41 |
| 10 | 36 |
| 11 | 38 |
| 12 | 37 |
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des âges, soit
et
Attention au fait que dans ce cas, le tableau représente un échantillon de la population cible totale (les astronautes en général) et l'on utilise la formule de l'écart-type pour échantillon (on divise par n -1) et non de l'écart-type pour population (où l'on divise par n).
Nous obtenons
Ensuite, sous excel par exemple, en appliquant la formule =LOI.STUDENT.BILATERALE(t
;
ddl)" avec le
t
que l'on vient de calculer et
ddl
=12-1=11 degrés de libertés, on trouve
p
=0.15820928.
Pour un test du t, la question suivante à se poser concerne le caractère bilatéral ou non du test. Ici, on a une hypothèse précisant que la moyenne attendue doit être supérieure à 38. C'est bien le cas puisque la moyenne observée est 39.25. Nous sommes donc fondés à travailler en unilatéral et nous divisons simplement la valeur p précédente par 2, ce qui donne 0.08508. Finalement, on peut rapporter le résultat inférentiel, conformément aux normes :
t (11)=1.51, p =.079 en unilatéral, ce qui n'est pas significatif, mais indique néanmoins une tendance.
2.3. Comparer deux échantillons indépendants.
Puisque l'on a deux groupes de sujets, on a aussi deux moyennes m1 et m2 . L'hypothèse nulle revient à poser que m1 = m2. Un test significatif indiquera que les données ne sont pas très compatibles avec l'hypothèse nulle et donc qu'on a plus probablement m1 ≠ m2.

Préalables spécifiques de cette version du test de Student :
- 1. Il faut soit avoir deux échantillons de données recueillies sur deux groupes de sujets différents.
- 2. Les données devraient idéalement être normalement distribuées.Cliquez ici pour voir comment tester la normalité de la distribution.
- 3. Les variances des échantillons réels devraient idéalement être homogènes. Sous SPSS ou Statistica par exemple, le "test de Levene" ne doit pas être significatif. Toutefois cette condition n'est pas rédhibitoire car les logiciels donnent alors des valeurs de p corrigées, selon des méthodes que nous ne détaillerons pas ici. Il suffit de vérifier l'homogénéité. Sous SPSS par exemple, si le test de Levene est significatif, on prendra alors la valeur de p calculée pour les variances non homogènes.
A. Calculer la valeur de
t
A.1. Pour les pressés : "En bref"
Liens de pratique avec un logiciel de statistiques : Voir ici des vidéos et textes pratiques
Soient deux échantillons réels, respectivement d'effectifs, moyennes et écarts-types
n1
,
m1,
s1
, et
n2
,
m2
,
s2
.
On commence par calculer l'erreur standard ESv de l'échantillon virtuel constitué par les deux échantillons indépendants :
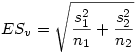
Et ensuite le t est donné par la formule
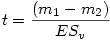
On présente le résultat en écrivant t(ddl)=n.nn (pour la présentation de la valeur p , voir l'article général sur la norme APA de présentation d'une valeur p).
A.2. Pour ceux qui aiment comprendre : D'où cela vient-il ?
Dans le test du t de Student, la statistique calculée est précisément la valeur t. Dans le cas de la comparaison de deux échantillons indépendants, voyons quelle formule employer. Commençons par rappeler la formule générale du t :
Soient mv la moyenne d'un échantillon virtuel de taille nv et ESv son erreur-standard, on a
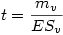
Ici notre échantillon virtuel est composé des deux échantillons indépendants réels. Sa moyenne est mv = (m1 - m2) où m1 et m2 sont les moyennes des deux échantillons réels.
Le calcul de ESv l'erreur standard de l'échantillon virtuel est moins naturel. En effet, ces deux échantillons étant indépendants, ils renvoient à des effectifs de taille potentiellement différentes et l'erreur standard de deux échantillons de tailles différentes ne s'obtient malheureusement pas en faisant simplement la moyenne des erreurs-standards. L'écart-type de l'échantillon virtuel issu de deux échantillons de tailles n1 et n2, de moyennes m1 et m2, et d'écarts-types s1 et s2 peut s'obtenir de la façon suivante :
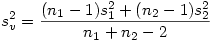
On produit alors l'ES standard de l'échantillon virtuel par la formule
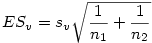
Finalement, il ne reste plus qu'à calculer
t
:
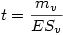
B. Comment obtenir la valeur p associée ?
Il nous faut connaître la valeur t et le ddl nombre de degrés de libertés.
Si elle n'est pas directement donnée par votre logiciel de statistique, la valeur p associée s'obtient
- soit en regardant dans une table du t de Student en prenant comme entrée la valeur du t ainsi calculée et comme nombre de degrés de libertés la valeur n-1 où n est le nombre de mesures.
- Soit au moyen d'une formule de tableur sous Microsoft Office Excel ou OpenOffice Calc : "=LOI.STUDENT.BILATERALE( t ; ddl )"
Par défaut, on travaillera en bilatéral et on se contentera de la valeur
p
précédemment obtenue.
Si toutefois on dispose d'une hypothèse orientée et que les statistiques descriptives vont dans le sens attendu (typiquement, on s'attend à ce que m1 > m2 et c'est le cas au niveau descriptif, ou bien on s'attend à ce que m1 < m2 et c'est le cas au niveau descriptif), alors on peut travailler en unilatéral : il suffit alors de prendre la valeur p précédemment obtenue et de la diviser par 2 avant de décider si le test est significatif ou non.
C. Un exemple
Supposons que l'on ait une hypothèse théorique (fictive) selon laquelle les premiers astronautes envoyés devraient avoir plus de 38 ans en moyenne, mais que ceux envoyés après une certaine date sont plus jeunes. Imaginons que la seule information dont nous disposions est l'âge des astronautes au moment de leur sortie sur notre satellite, et supposons encore que 6 de ces astronautes appartiennent au premier groupe, et les 6 autres au deuxième groupe. Nous obtenons le tableau suivant :
| Individu | Groupe |
Age
|
| 1 |
1
|
32 |
| 2 | 1 | 38 |
| 3 | 1 | 36 |
| 4 | 1 | 37 |
| 5 | 1 | 42 |
| 6 | 1 | 26 |
| 7 | 2 | 39 |
| 8 | 2 | 35 |
| 9 | 2 | 33 |
| 10 | 2 | 34 |
| 11 | 2 | 37 |
| 12 | 2 | 36 |
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des âges pour chacun des deux groupes, soit
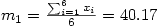
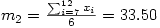
et
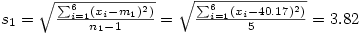
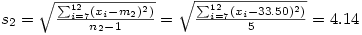
Attention au fait que dans ce cas, le tableau représente un échantillon de la population totale des astronautes et l'on utilise la formule de l'écart-type pour échantillon (on divise par n -1) et non de l'écart-type pour population (où l'on divise par n).
L'écart-type de l'échantillon virtuel issu de deux échantillons de tailles n1 et n2, de moyennes m1 et m2, et d'écarts-types s1 et s2 peut s'obtenir de la façon suivante :
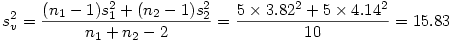
Il ne reste alors qu'à produire l'ES de l'échantillon virtuel par la formule
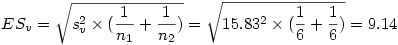
Finalement, il ne reste plus qu'à calculer
t
:
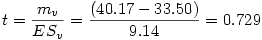
Ensuite sous Excel par exemple, en appliquant la formule =LOI.STUDENT.BILATERALE(t ; ddl)" avec le t que l'on vient de calculer et ddl=6+6-2=10 degrés de libertés, on trouve p =0.48255927.
Pour un test du t , la question suivante à se poser concernerait le caractère bilatéral ou non du test. Ici, de toute façon, même si on divisait par deux la valeur de p, on serait encore très largement au dessus du seuil de signification, donc ce n'est pas la peine d'aller plus loin : le test n'est pas significatif et l'on ne peut pas conclure qu'il existe une différence entre les groupes.
On pourra rapporter le résultat en disant que "t(10)=0.73, ns" (norme APA 6e édition), ou mieux en rapportant la valeur p arrondie à deux ou trois décimales (norme APA 7e édition).
- 1. Il faut soit avoir deux échantillons de données recueillies sur deux groupes de sujets différents.
- 2. Les données devraient idéalement être normalement distribuées. Cliquez ici pour voir comment tester la normalité de la distribution.
- 3. Les variances des échantillons réels devraient idéalement être homogènes. Sous SPSS ou Statistica par exemple, le "test de Levene" ne doit pas être significatif. Il est alors souhaitable d'utiliser la variante dite "test de Welch", qui est disponible dans jamovi et est même le test de Student par défaut dans R.
2.4. Comparer deux échantillons appariés.
L'hypothèse nulle est ici la suivante :
m
1
=m
2
. Ou encore, ce qui revient au même,
m
1
-m
2
=0. Par exemple, si l'on a fait une comparaison avant-après, en faisant la différence des deux valeurs obtenues pour chaque sujet, on obtient une nouvelle variable qu'il suffit de comparer, par un test à un échantillon vu précédemment, contre la valeur de référence 0. On pourra ensuite interpréter la différence en termes de progression : si la moyenne est significativement supérieure à 0 il y aura eu augmentation, si la moyenne est significativement inférieure à 0 il y aura eu diminution. Enfin, si la différence n'est ni significativement supérieure ni significativement inférieure à zéro, on ne peut pas dire qu'il y a un effet avant-après.
Préalables spécifiques de cette version du test de Student :
1. Il faut avoir deux échantillons d'un même type de mesure (par exemple, un temps de réponse dans les deux cas) recueillis à raison de deux données par individu statistique et sur lesquelles on peut procéder à une différence.
2. Les données de l'échantillon devraient idéalement être normalement distribuées. Cliquez ici pour accéder à l'article expliquant comment vérifier si cette condition est réalisée.
2.1. Obtenir la valeur de
t
2.1.1. Pour les pressés : "En très bref"
À partir des deux échantillons de données appariées, on construit la variable de différence en calculant pour chaque ligne i , la valeur xi = x i1 - xi 2 . Cela nous donne un échantillon réel de taille n (ici n couples de données), de moyenne m et d'écart-type s.
Selon les informations dont on dispose, on applique la formule avec l'erreur standard ES,
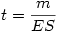
ou, ce qui revient au même, celle avec l'effectif et l'écart-type d'échantillon,
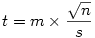
On présente le résultat en écrivant t ( ddl )=n.nn (pour la présentation de la valeur p , voir l'article général sur la norme APA de présentation ).
2.2. Comment obtenir la valeur p associée ?
Il nous faut connaître la valeur t bien sûr et le nombre de degrés de liberté.
Ici l'échantillon virtuel a la même taille que l'échantillon réel, soit n individus. Le nombre de degrés de liberté est directement ddl=n -1.
Si elle n'est pas directement donnée par votre logiciel de statistique, la valeur p associée s'obtient
- soit en regardant dans une table du t de student en prenant comme entrée la valeur du t ainsi calculée et comme nombre de degrés de liberté la valeur n -1 où n est le nombre de mesures.
-
Soit au moyen d'une formule de tableur sous Microsoft Office Excel ou OpenOffice Calc : "=LOI.STUDENT.BILATERALE(
t
;
ddl
)"
2.3. Unilatéral ou bilatéral ?
Par défaut, on travaillera en bilatéral et on se contentera de la valeur p précédemment obtenue.
Si toutefois on dispose d'une hypothèse orientée et que les statistiques descriptives vont dans le sens attendu (typiquement, on s'attend à ce que m > 0 et c'est le cas au niveau descriptif, ou bien on s'attend à ce que m < 0 et c'est le cas au niveau descriptif), alors on peut travailler en unilatéral : il suffit alors de prendre la valeur p préalablement obtenue et la diviser par 2 avant de décider si le test est significatif ou non.
2.4. Un exemple
Dans une expérience sur le risque lié à l'alcool, on a demandé à chacun des 31 participants d'évaluer le risque associé à une situation de conduite sur une échelle de 1 à 5.
On a obtenu, en rangeant les données à raison d'une ligne par sujet, le tableau suivant :
| Sansalcool | Avec alcool | Différence |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 4 | 3 |
| 1 | 4 | 3 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 2 | 5 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 4 | 3 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 2 | 4 | 2 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 3 | 2 |
| 2 | 5 | 3 |
| 1 | 5 | 4 |
| 1 | 3 | 2 |
| 1 | 5 | 4 |
| 1 | 5 | 4 |
| 1 | 3 | 2 |
| 1 | 4 | 3 |
En première approximation, on a constaté que la moyenne de la situation sans alcool est de 1.10 alors que la colonne 2 est en moyenne à 4.52. Descriptivement, on pourrait donc dire que les participants jugent la situation 2 plus risquée que la situation 1... mais est-ce vrai statistiquement ?
La troisième colonne a été obtenue en faisant la différence de la colonne 2 (avec alcool) et de la colonne 1 (sans alcool). Nous allons travailler à partir de cette colonne.
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des différences, soit
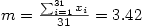
Pour ceux qui se rappellent que la moyenne des différences est égale à la différence des moyennes (les effectifs étant ici égaux), cette moyenne est sans surprise puisque 5.52 - 1.10 = 3.42.
Pour l'écart-type,
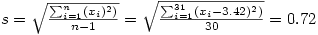
Nous obtenons
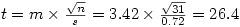
Ensuite sous Excel par exemple, en appliquant la formule =LOI.STUDENT.BILATERALE( t ; ddl )" avec le t que l'on vient de calculer et ddl=31-1=30 degrés de libertés, on trouve p =2.4x10 -22, ce qui est quasiment égal à zéro. Autrement dit, ce n'est même pas la peine de se poser la question de la latéralité : de toute façon le test est très nettement significatif.
Finalement on peut rapporter le résultat, conformément aux normes :
t (30)=26.4, p< .001, ce qui est significatif : on peut donc conclure que la situation 2 est jugée plus risquée par les participants que la situation 1.
3. Comparer plus de deux moyennes : L'ANOVA à un facteur
Objectifs. Mettre l'étudiant en position de savoir quand et comment réaliser une comparaison de moyennes à plus de deux groupes.
Prérequis.
- Cours de L1
- Approche intuitive de l'inférence statistique
- Hypothèse nulle
- Principe général de la comparaison de moyennes.
- t de student

Ronald Fisher (1890-1962), inventeur de l'ANOVA
Résumé.
Une table d'orientation guide l'exploration du test. Pour les "utilisateurs pressés", une entrée permet d'accéder directement à un formulaire simplifié. Pour ceux qui veulent comprendre, on expose la technique générale de l'ANOVA à un facteur.
3.1. Table d’orientation pour l'ANOVA À 1 FACTEUR
Veuillez choisir ci-dessous l’utilisation que vous souhaitez faire de cet article.
- Comprendre la logique générale de l'ANOVA à un facteur. J’ai plusieurs groupes d'individus statistiques correspondants aux différentes modalités de la variable indépendante, et pour chaque individu, j'ai une mesure de la variable dépendante.
- Comprendre la comparaison globale. Je veux voir si globalement, on peut dire qu'il existe un effet de la variable indépendante sur la variable dépendante.
- Comprendre la comparaison planifiée de moyennes. J'avais avant même de faire le test global une hypothèse sur l'existence d'une différence entre certains groupes de sujets de mon recueil. Je veux tester cette hypothèse.
- Comprendre les tests post-hoc. Bien que je soupçonnais une relation globale, je n'avais pas d'hypothèse a priori sur les comparaisons entre les groupes. Je veux néanmoins savoir s'il existe des paires de groupes telles que l'un des groupes est significativement différent de l'autre.
1. Dans quel cas appliquer un tel test ?
Objectif. Le test de l'ANOVA s'applique lorsque l'objectif est de comparer plus de deux moyennes entre elles (si seules deux moyennes sont à comparer, on préférera le test du t de student).
Type des informations disponibles : L'ANOVA à un facteur s'applique lorsque la VI est une variable nominale (ses modalités sont des catégories indépendantes) ou ordinales (ses modalités peuvent être rangées) mais pas lorsque ses modalités sont numériques. Dans ce dernier cas, c'est généralement la régression linéaire qui s'applique. Les valeurs mesurées pour la VD doivent être numériques, faute de quoi l'idée même de moyenne n'a pas de sens.
Distribution des observations : Les données doivent être normalement distribuées.
Condition d'indépendance : Les données doivent être indépendantes (les données d'un sujet ne sont pas censées avoir influencé les mesures faites sur un autre sujet).
3.2. Philosophie de l'ANOVA à un facteur

Inventée au début du XX e siècle par Ronald Fisher, pour résoudre des problèmes de... rendements agricoles, l'analyse de variance (ou ANOVA pour ANalysis Of VAriance) a initialement été conçue pour traiter le problème de la prédiction et de l’explication des variations que l’on constate dans les données expérimentales. Dans le cas de Fisher, il ne s’agissait pas de variations humaines, mais de la quantité récoltée dans des champs expérimentaux où l’on testait diverses méthodes agricoles. Avant Fisher, on savait construire des expériences, comme en physique, mais on ne savait pas comment faire pour traiter statistiquement le problème de la variabilité.
Les types de variations
L’ANOVA distingue plusieurs types de variations :
• Les variations systématiques inter-groupes, c’est-à-dire liées à l’effet d’un facteur commun à un groupe d’observations (par exemple, l’effet du divorce sur la réussite scolaire des enfants : on compare des enfants de parents divorcés vs. non divorcés).
• Les variations systématiques intra-groupes , spécifiques aux individus sur lesquels on a fait les mesures (par exemple, parmi le groupe des enfants de parents divorcés certains sont plus travailleurs que d'autres) mais sans rapport avec la répartition des individus dans les différents groupes.
• Pour être complets, dans le cas des analyses "à mesures répétées", que nous ne voyons pas ici, il faudrait aussi ajouter les variations systématiques intra-individuelles, c’est-à-dire qui surviennent pour un même individu sur lequel on procède à plusieurs mesures.
• Les variations aléatoires (erreurs de mesure, aléas dans les autres éléments qui déterminent la quantité mesurée, etc.).
Du point de vue expérimental (et statistique), les variations aléatoires sont une gêne que l’on peut réduire en faisant la moyenne de nombreuses observations. Pour des explications plus détaillées sur les types de variations et leurs significations, consulter les différents articles consacrés à ce sujet dans le cours de L1.
ANOVA et recherche de causalités
L’ANOVA est une méthode de comparaison de moyennes qui suppose qu'il existe peut-être un lien entre une cause et un effet. De façon générale, on sait que s’il existe un lien entre une cause hypothétique et un effet, alors quand la cause varie, l’effet doit varier aussi. L’ANOVA va donc examiner les variations pour vérifier s’il est plausible d’attribuer les variations observées d’un effet (e.g. la plus ou moins bonne réussite scolaire) aux variations d’une cause hypothétique (e,g, le divorce ou non des parents).
- La variable qui mesure les variations de la cause est appelée Variable Indépendante (VI) ou Facteur. Moyen mnémotechnique : on l'appelle "Indépendante" car la cause ne dépend pas de l'effet.
- La variable qui mesure les variations de l'effet est appelée Variable Dépendante (VD). Moyen mnémotechnique : cette variable est dite « dépendante » car l'effet dépend de la cause.
Dans l’ANOVA, les variations pertinentes de la cause sont représentées par les différences entre les modalités de la VI, donc par le fait pour un sujet d’appartenir à tel ou tel groupe ;
p
our l’effet, les variations pertinentes sont celles de la VD. À partir de là,
- L’hypothèse de relation causale, dans l’ANOVA, est que si l’on compare les sujets de groupes différents, la moyenne observée de la VD sera différente selon les différents groupes. Ainsi, par exemple, suivant que des individus ont bénéficié ou non d’une thérapie cognitive (variation de la cause), leur degré de phobie s’est réduit pas du tout, un peu, ou beaucoup (variation de l’effet).
- L’hypothèse nulle pour l’ANOVA est que les différences observées entre les moyennes des différents groupes quant à la VD seront si petites qu’elles pourront s’expliquer facilement par le hasard. Par exemple, si l’on compare le niveau de réussite professionnelle d’individus de signes astrologiques différents, on devrait trouver que les différences de signes astrologiques n’expliquent pas mieux les revenus que ne le ferait le hasard (on ne peut pas rejeter l’hypothèse nulle).
Bien sûr, pour comprendre réellement l'ANOVA, il faut en comprendre la mécanique. Il s'agit donc de comprendre comment sont réparties les sources de variation.
Décomposition des sources de variations
Du point du vue de la statistique en général, les principales sources de variation sont les variations aléatoires et systématiques. Mais du point de vue de l’ANOVA, il faut approfondir l’analyse des variations systématiques, en distinguant celles qui sont dues au facteur étudié (donc des variations inter-groupes) et celles qui sont dues à autre chose. À cet égard, les variations purement aléatoires, et les variations systématiques intra-groupes seront donc traitées statistiquement de la même façon car toutes renvoient à autre chose qu'au facteur étudié.
Dans l’ANOVA, on considère que les variations se traduisent par une grandeur mathématique, la variance. L’idée globale est alors que si le facteur a vraiment un effet, la part des variations qu’on peut lui attribuer sera significativement plus élevée que la part des variations qu’on ne peut pas lui attribuer. Autrement dit, on va décomposer la somme globale des variations (qui sera évaluée par la variance totale) en
- une partie attribuable au facteur (qui sera évaluée par la variance inter-groupe) et
- une partie attribuable à autre chose (qui sera évaluée par la variance intra-groupes).
C'est le rapport des deux qui permettra ensuite l'inférence statistique :si la variance inter-groupe est grande devant la variance intra-groupe,c'est probablement que l'hypothèse nulle est fausse car l'effet du facteur est massif, si au contraire la variance inter-groupe est petite devant la variance intra-groupes, c'est que les fluctuations imprévues expliquent mieux les données et l'hypothèse nulle devient difficile à rejeter.
On voit donc que toute la méthode va consister à répartir les variations entre leurs différentes sources de façon à pouvoir calculer ce rapport des deux variances, celle expliquée et celle non expliquée. D’où le nom global de la méthode : Analyse de la Variance.
3.3. Variations et variance dans l'ANOVA
A. La variance : formule générale classique

Nous l'avons dit, les variations sont ici mesurées par la variance, dont nous rappelons que la formule générale pour la variance
s²
d'un échantillon de mesures stockées dans une colonne de données
X
et dont la moyenne est 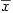 .
.
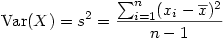
Autrement dit, si l'on suit cette formule, on va...
- pour chacune des n observations de l'échantillon que l'on considère, calculer l'écart qui existe entre cette observation et la moyenne du groupe entier,
- passer cet écart au carré puis
- faire une sorte de moyenne de tous ces écarts carrés.
J'écris ici une sorte de moyenne car pour faire une vraie moyenne il aurait fallu en diviser la somme par n alors que nous divisons par n -1 pour des raisons formelles liées au fait qu'on travaille sur un échantillon et non sur la population entière.
B. La variance n'est pas " additive "
À cet instant, il faut nous souvenir que nous cherchons à attribuer l'ensemble des variations constatées de la VD à l'une de deux sources de variations possibles : les variations dues au facteur étudié (variations inter-groupes) et celles dues à d'autres déterminants inconnus (variations intra-groupes).
Puisque dans l'ANOVA on représente les variations par la variance, nous avons donc trois types de variance :
- À l'ensemble total des variations, on pourra attribuer une variance Totale.
- À l'ensemble des variations dues au facteur, nous ferons correspondre une variance inter-groupes (on dit parfois aussi Variance du Traitement).
- Aux variations que l'on ne sait pas expliquer, nous ferons correspondre une variance d'erreur, appelée aussi, variance résiduelle ou encore variance intra-groupes.
Si l'on veut pouvoir attribuer dans nos données la part qui revient à chaque type de variation, il nous faut donc connaître la relation qui unit la variance totale, la variance d'erreur et la variance du traitement. Malheureusement, la variance n'est pas additive : dans le cas général
Var Totale ≠ (Var Traitement + Var Erreur )...
Ce n'est donc pas pratique à manipuler et c'est pourquoi, dans le détail des calculs, nous passerons par une notion légèrement différente, la notion de "Somme des Carrés".
3.4. Somme des carrés et carré moyen
A. Relations entre Somme des carrés, Variance et Carré moyen
On appelle Somme des carrés (SC en abrégé en français, ou encore SS pour "Sum of Squares" en anglais), le numérateur de la formule générale de la variance. La formule générale de la variance peut donc se ré-écrire :
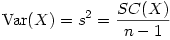
Nous avons vu dans le cours sur le t de Student que le nombre de degrés de liberté de la moyenne d'un groupe de mesures est égal au nombre de sujets - 1
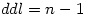
Du coup, on peut réécrire ainsi la formule précédente
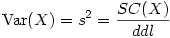
On appellera alors cette expression le carré moyen de l'échantillon, que l'on abrégera par CM en français et MS pour Mean Square en anglais.
Le carré moyen n'est donc qu'un autre nom pour la variance d'échantillon et c'est ce carré moyen qui est généralement présenté dans les tableaux d'analyse de variance fournis par les logiciels de statistique.
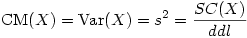
Attention : dans certains tableaux, il existe des formules de la variance d'échantillon et des formules de la variance de population. Si vous calculez vos sommes de carrés à partir de ces formules (puisqu'il suffit de multiplier le carré moyen, donc la variance, par le nombre de degrés de libertés pour avoir la somme des carrés) ne vous trompez pas et utilisez la variance d'échantillon, car dans la variance de population la somme des carrés n'est pas divisée par le nombre de degrés de libertés ( N -1) mais par l'effectif complet (N).
B. Des "Types" de sommes de carrés ??
Dans les logiciels de statistique, vous trouverez mentionnée l'existence de sommes des carrés "de type III" ou "de type VI". Il s'agit là de raffinements de la notion de calcul des sommes de carrés dans les ANOVA à plusieurs facteurs lorsque les plans sont déséquilibrés (les effectifs entre les groupes sont inégaux). Ce n'est pas du niveau du présent cours et nous nous bornerons ici à en signaler l'existence.
3.5. Décomposer la somme des carrés
Pourquoi nous intéresser à la somme des carrés, qui n'est après tout qu'un morceau de l'équation de la variance ?
Rappelons que nous cherchons à attribuer l'ensemble des variations constatées de la VD à l'une de deux sources de variations possibles : les variations dues au facteur étudié (variations inter-groupes) et celles dues à d'autres déterminants inconnus (variations intra-groupes). Le problème était que la variance n'est pas additive, car dans le cas général on n'a PAS le droit d'écrire que Var Tot = Var Inter + Var Intra .
Et c'est là tout l'intérêt de raisonner à partir de la notion de somme des carrés car la somme des carrés possède une propriété cruciale que n'a pas la variance : Elle permet d'écrire l'équation très intéressante suivante :
SCtotale = SCTraitements + SCerreur
À partir de là,
-
si l'on sait calculer deux des trois sommes de carrés, on peut très facilement retrouver la troisième. Or, nous verrons que la
SC
Totale
et la
SC
Traitements
sont très faciles à calculer. Il suffit alors de retourner l'équation pour avoir la
SC
erreur
:
SCerreur = SCtotale - SCTraitements - si l'hypothèse nulle est vraie, alors la somme des carrés totale est égale dans le principe à la somme des carrés de l'erreur et la somme des carrés du traitement est nulle. Bien sûr, dans la pratique, on n'a quasiment jamais cette observation idéale. Néanmoins, elle peut servir de référence pour voir à quel point les résultats s'écartent de ce que donnerait l'hypothèse nulle si elle était vraie. Nous reviendrons sur ce point lors du calcul de l'inférence statistique.
Pour le moment, regardons comment calculer la première somme des carrés, la SCTotale.
3.6. Calculer la somme des carrés totale
Imaginons que nous fassions une ANOVA où l'effet du facteur G est étudié au travers de mesures prises sur k groupes, dont les effectifs sont respectivement n1, n2, ... , nk . Soit un effectif global N = n1 + n2 +...+ nk.
Il s'agit de capturer l'ensemble de toutes les variations, c'est-à-dire l'ensemble des variations de toutes les mesures de tous les groupes. S'il n'y avait aucune variation, L'échantillon global (composé des échantillons issus de chaque groupe) aurait exactement la valeur globale de la population étudiée, et donc la moyenne de l'échantillon global serait égale à la moyenne générale de la population. De plus, toujours dans ce monde hypothétique, chacun des différents groupes aurait la même moyenne que la moyenne de l'ensemble de tous les groupes.
Donc pour calculer la variance associée aux variations totales, il faut calculer les écarts à la moyenne générale de toutes les mesures ("Grand Mean" en anglais), quel que soit le groupe d'où proviennent les mesures.
Et la somme des carrés totale est donc tout simplement liée à la variance totale de toutes les mesures de la VD.
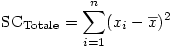
Le nombre de degrés de liberté associés à cette somme de carrés est le nombre total de sujets - 1 :
ddlTotal = N - 1
Le CM totale s'obtient en divisant la SC Totale par le ddl Total.
CMTotal = SC Total / ddl Total
Voyons un exemple numérique sur des données fictives :
La colonne X contient les notes de chaque élève, quel que soit leur groupe. Le total de toutes ces notes est 167. Il y a 16 notes, donc la moyenne générale (Grand Mean en anglais) est 167/16 = 10.4375
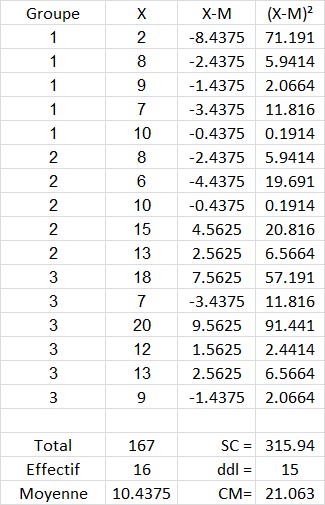
Pour chacune de ces notes, on place dans la colonne intitulée ici X-M l'écart entre la note et la moyenne générale, puis dans la colonne suivante, nommée " (X-M)² ", on passe cet écart au carré. Bien sûr, on aurait pu tout mettre en une seule formule, mais il s'agit ici d'illustrer le détail du calcul.
La somme de cette dernière colonne est la somme des carrés totale, soit 315.9375, arrondie sur l'image à 315.94.
Le nombre de degrés de liberté est l'effectif total - 1, soit 15.
Le carré moyen s'obtient en divisant l'un par l'autre, soit 315.9375/15 = 21.063.
Vous pouvez vérifier aisément au moyen d'une formule de tableur que ce carré moyen est directement donné par la variance de l'échantillon des 16 mesures.
3.7. Calculer la somme des carrés inter-groupes (SC du facteur)

Dans une ANOVA, le "facteur" (aussi appelé "traitement") correspond à la répartition des sujets en différents groupes expérimentaux. "L'effet du facteur" résidera donc dans le fait que les groupes auront des moyennes plus ou moins différentes.
Pour comprendre l'analyse qui sera faite, il faut savoir que si l'on considère la réponse d'un sujet donné, on peut considérer qu'une partie de son score est due au fait que c'est un sujet issu de la population générale, qu'une autre partie est due au fait qu'il appartient à tel groupe, et enfin qu'une dernière partie résulte de facteurs aléatoires qu'on ne connaît pas. S'il n'y avait pas de variation aléatoire, tous les sujets d'un même groupe auraient produit la même valeur. Et cette valeur serait la moyenne du groupe. De ce fait, l'effet du facteur est l'écart entre la moyenne du groupe et la moyenne générale.
Pour l'analyse en termes de sommes des carrés, il faut donc remplacer la mesure de chaque individu du groupe par la valeur moyenne du groupe. Puis calculer la somme des carrés de la même façon que la somme des carrés totale.
6.1. Approche intuitive
Reprenons l'exemple numérique vu dans le calcul de la SC Totale :
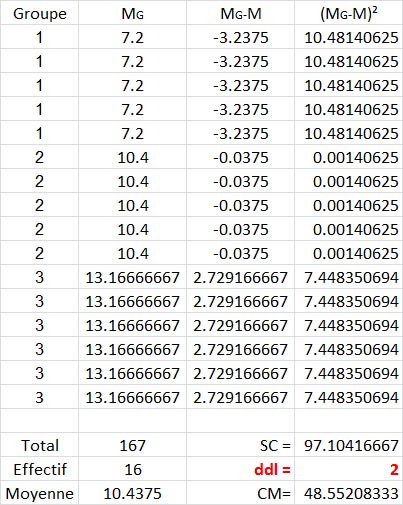
Vous voyez qu'on a remplacé chaque valeur individuelle (l'ancienne colonne "X") par la valeur de la moyenne du groupe (Colonne "M G "), par exemple, 7.2 pour les données du groupe 1). La moyenne générale M est ensuite retirée de la moyenne du groupe (Colonne "MG - M") pour chaque individu et le tout passé au carré selon le même principe que pour la somme des carrés totale (Colonne "(MG - M)²"). La somme de tous ces écarts carrés est la SCInter soit ici 97.10416667.
Attention !! Le nombre de degrés de liberté en revanche n'est pas (16 - 1) mais (3 groupes - 1), soit 2 (en rouge sur l'image) !! Du coup le carré moyen est la somme des carrés divisée par 2 et non par 15 !!
6.2. Approche formelle
Pour les étudiants désireux d'une approche plus formelle, voici des formules qui exposent la démarche. En notant la moyenne générale des N sujets
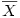
et en notant la moyenne du k ième groupe (c'est-à-dire du groupe Gk)
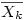
on aura alors pour les nk individus du groupe k la somme des carrés suivante :
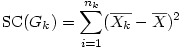
ou, ce qui revient au même,
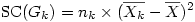
Vous noterez que cette formule ne préjuge pas de l'équilibre des effectifs, c'est-à-dire que si des groupes ont des tailles différentes, la somme des carrés d'un groupe sera proportionnelle à son effectif.
Finalement, on somme les SC de chacun des groupes pour obtenir la somme des carrés du facteur :
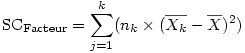
Le nombre de degrés de liberté associés à cette somme de carrés est le nombre de groupes - 1. Donc si l'on suppose un facteur à k groupes, on a
ddlFacteur = ddl Inter = k - 1
3.8. Calculer la somme des carrés intra-groupes
7.1. Option simple : par différence
Il suffit de faire la différence des deux précédentes sommes de carrés :
SCIntra = SCtotale - SCInter
Le nombre de degrés de liberté associés peut lui aussi s'obtenir en faisant la différence entre le nombre de degrés de liberté de la SCTotale et le nombre de degrés de liberté de la SCInter. Soit,
ddlIntra = ddlTotal - ddlInter = (N - 1) - (k - 1),
Et donc finalement
ddlIntra = N - k

Sur l'exemple, vous pouvez vérifier facilement que la SCintra est la différence des deux autres, et qu'il en va de même pour les ddlintra. Bien sûr, le CM ne peut se calculer aussi par différence, il faut rediviser la SCIntra par les ddlIntra.
7.2. Option complexe : directement
On peut aussi calculer les choses directement, si vous voulez vérifier les calculs par exemple.
Pour ce faire, on considère chaque groupe comme s'il était complètement indépendant des autres. On calcule la somme des carrés exactement de la même façon que la somme des carrés totale, mais en appliquant la formule aux seules données du groupe. Il suffit ensuite de sommer les SC obtenues indépendamment sur chacun des groupes pour avoir la SCInter.
Chaque groupe est alors associé à un nombre de degrés égal à son effectif - 1, soit Nk - 1 et le nombre de degrés de liberté associés à la SCIntra s'obtient en faisant la somme des k groupes, ce qui donne N1 - 1 + N2 - 1 +... + Nk - 1, soit encore N1 + N2 + ... + Nk - 1 - 1 -... - 1 (on enlèvera k fois 1, donc au total, k), et donc puisque N1 + N2 + ... + Nk = N, on obtient bien ddlInter = N - k.
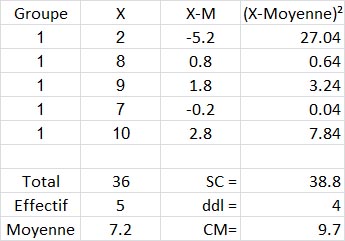
Reprenons notre exemple numérique :
Pour le groupe 1 nous avons :
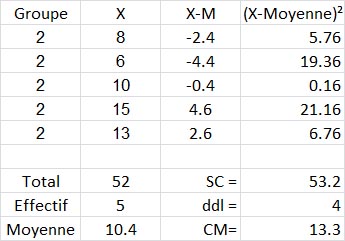
Pour le groupe 2 nous avons :
Pour le groupe 3 nous avons :
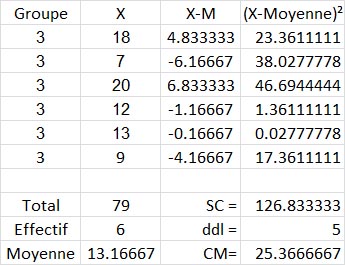
Et, finalement, nous faisons la somme des SC issues des trois tableaux précédents, nous trouvons SCIntra =38.8+53.2+126.83, soit 218.83.
Et pour les ddlIntra , nous avons bien 4+4+5=13.
3.9. ANOVA et calcul des valeurs-p
8.1. Calcul de la valeur
F
Si l'on calcule le rapport entre la variance intra-groupe et la variance totale, la statistique obtenue, que l’on appelle F , suit une loi dite de Loi de Fisher-Snedecor.
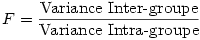
Et puisque dans l'ANOVA la variance est donnée par le carré moyen, pour obtenir le F nous n'avons qu'à faire la division du CM Inter par le CM Intra . L'exemple numérique précédent est clair dans le tableau de résumé de l'ANOVA :
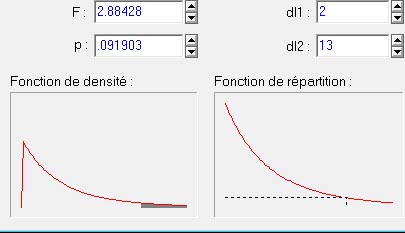
F = 48.552 / 16.833 = 2.88428
8.2. Obtention du
p
à partir du
F
8.2.1. Principe
La loi normale utilise deux paramètres : la moyenne et la variance. La loi normale centrée-réduite n'en a plus aucun, car il s'agit de la loi normale pour lesquelles la moyenne a été fixée à 0 et l'écart-type à 1. La loi de Student représente une sorte de famille de variantes de la loi normale centrée réduite, où chacune des variantes est déterminée par la valeur d’un paramètre particulier, le nombre de degrés de liberté. Ainsi pour chaque degré de liberté, on peut calculer une loi de Student particulière. Dans le cas de la loi du F , les choses gagnent un cran de complexité puisque la loi du F est une famille de variantes dont chacune est déterminée, non par un seul mais par deux degrés de liberté. Spécifiquement, il s’agit (1) du nombre de degrés de liberté du facteur, qui est tout simplement donné par le nombre de groupes – 1 ;et (2) le nombre de degrés de liberté intra-groupes, ou "nombre de degrés de liberté de l’erreur", qui est le nombre de sujets moins le nombre de groupes.
Partant de là, en appliquant les mêmes principes que nous avons déjà vus à propos de la loi normale, ou de la loi de Student, on peut mettre en relation une valeur donnée de F, celle observée dans les données, avec la probabilité a priori de rencontrer une telle valeur, probabilité qui nous est donnée par la loi.
Si nous prenons la valeur du F de l'exemple numérique précédent, voici ce que nous obtenons (image générée à partir du logiciel Statistica) :

Le graphique en bas à gauche de la figure ci-dessus représente la courbe de la distribution théorique du F de Fisher pour une variance inter à 2 degrés de liberté et pour 13 degrés de liberté intra. La petite région grisée sous la courbe représente la surface relative occupée par les valeurs de F qui sont supérieures ou égales à la valeur indiquée (2.88428). On voit que plus ce F est grand, et plus la surface grisée représentera une proportion faible de la courbe. Ici cela représente 9,903% de la surface totale de la courbe : la probabilité d'obtenir par hasard une valeur de F supérieure ou égale à celle que nous avons calculée à partir de nos données n'est que .091903 (valeur p indiquée en haut dans la figure). Dans ce cas, cette valeur n'est pas significative au seuil de 5% puisque le risque pris en rejetant l'hypothèse dépasse 5%, ce qui n'est pas acceptable dans les conventions classiques.
Il existe des tables de cette loi, mais de nos jours les logiciels de statistique et même les logiciels tableurs (eg., Microsoft Excel, ou OpenOffice Calc) donnent directement la valeur p . Par exemple, sous Excel, la fonction "=LOI.F(F;ddl1;ddl2)" où l'on remplace F, ddl1, et ddl2 par les paramètres que nous avons calculés précédemment, cette fonction donc retourne directement la valeur 0.091903.
8.2.2. Mise en garde concernant les tests unilatéraux
Une différence majeure existe entre d’un côté la loi normale et la loi de Student, et de l'autre côté la loi du F. Si nous regardons la forme de la loi du F (figure plus haut), nous voyons que cette loi n’est pas symétrique, contrairement aux deux précédentes. Cette caractéristique a une importance majeure d’un point de vue calculatoire : on ne peut pas appliquer la technique des tests unilatéraux avec des statistiques F comme on le faisait avec les tests t. Rappelons que le test unilatéral repose sur l’idée que l’hypothèse étant orientée, si les résultats observés vont dans le sens attendu, on peut diviser par deux la valeur p obtenue puisque seule la moitié de l’aire sous la courbe de la loi est pertinente. Cette possibilité n’a aucun sens pour la loi du F.
3.10. Comment présenter les résultats d'un test d'ANOVA ?
Nous nous basons ici sur les normes internationales en vigueur en psychologie, les normes de l'APA (American Psychological Association), 7e édition.
9.1. Les statistiques descriptives
Comme le test du t, l'ANOVA est avant tout une comparaison de moyennes, comparaison qui repose sur une ou des mesures de dispersion. Il faut donc impérativement rapporter les données de statistiques descriptives, dispersions comprises. Répétons-le, les statistiques inférentielles ne sont que des informations de second ordre, des indicateurs sur la fiabilité des résultats obtenus. Les informations de premier ordre, celles qui disent ce que l'on a vraiment observé, ce sont les statistiques descriptives et non les statistiques inférentielles !
Ces statistiques descriptives peuvent être présentées dans le texte du compte-rendu ou bien, le plus souvent, dans une table.
Lorsque l'on compare des groupes de tailles différentes, il est courant de donner comme indice de dispersion non pas la variance ou l'écart-type, qui sont très sensibles à la taille de l'échantillon, mais l'erreur standard qui l'est moins. On l'a dit plus haut, l'erreur standard s'obtient en divisant l'écart-type par la racine carrée de la taille de l'échantillon. Par exemple, si l'écart-type vaut 3.0 et qu'il y a 20 sujets, cela fait une erreur standard de 3/racine(20) = 0.67.
9.2. Les statistiques inférentielles.
Comme la distribution du F dépend de deux nombres de degrés de liberté, il convient donc de préciser ceux-ci lorsque vous rapportez vos résultats. Cela donne une structure de la forme suivante :
F (ddl1, ddl2)=n.nn; p =xxx.
- ddl1 est le nombre de degrés de liberté intra-groupe. C'est le nombre de groupes moins un.
- ddl2 est le nombre de degrés de liberté inter-groupes, aussi appelé degré de liberté de l'erreur. C'est tout simplement le nombre de sujets moins le nombre de groupes.
- la valeur n.nn peut se rapporter avec un signe ou non, mais en tous les cas il est inutile de rapporter plus de deux décimales. Les logiciels donnent souvent des valeurs ayant plus de décimales, mais en pratique rapporter plus de deux décimales reviendrait à communiquer une information qui n'a pas grand-sens.
Enfin, la façon de rapporter les valeurs de p est tout à fait conventionnelle et ne dépend pas du type de test utilisé 1 .
Ici, à partir de notre exemple numérique, nous écrirons F (2,13) = 2.88; p =.091
1. Selon les normes de publication en vigueur en psychologie scientifique, il est d'usage de rapporter, outre les valeurs de t et le p associé, une variable représentant ce qu'on appelle la taille d'effet. Le calcul de cette dernière et sa signification dépassent le cadre de ce cours, aussi la laisserons-nous de côté.
4. Introduction aux comparaisons planifiées dans une ANOVA
Objectifs. Exposer la limite de ce que nous apprend l'ANOVA globale ("omnibus"). Introduire la distinction entre tests planifiés et "post-hoc". Introduire ainsi les articles décrivant spécifiquement ces deux types de procédures.
Prérequis.
- Cours de L1
- Approche intuitive de l'inférence statistique
- Hypothèse nulle
- Principe général de la comparaison de moyennes
- t de student
- ANOVA à 1 facteur
Résumé. L'ANOVA globale dit si le facteur a un effet significatif, mais ne nous renseigne pas sur les comparaisons possibles entre deux ou plusieurs des groupes qui servent à opérationnaliser le facteur. Il faut pour cela procéder à des tests spécifiques, mais la nature des tests dépend des caractéristiques des hypothèses que l'on cherche à tester. Les procédures de "comparaisons planifiées" s'appliquent lorsque le chercheur a décidé les comparaisons à réaliser avant même de faire l'analyse globale. Les comparaisons "post-hoc" sont plus de nature exploratoire et servent à repérer des effets que l'on avait pas anticipés.
4.1. Les types de comparaisons possibles

Dans l'article précédent, nous avons appris à réaliser une ANOVA globale ou "omnibus". Le fond de l'ANOVA est de répartir les observations dans différentes conditions expérimentales et de regarder si les mesures prises dans l'ensemble des conditions peuvent être considérées comme égales ou non. L'hypothèse nulle est que toutes les moyennes en présence sont égales. Mais on s'intéresse souvent non pas à un ensemble global mais à des comparaisons plus spécifiques. En effet, supposons que nous ayons troisgroupes expérimentaux où l'on teste deux variantes d'une stratégie thérapeutique. Le groupe 1 où l'on a appliqué la thérapie A, le groupe 2où l'on appliqué la thérapie B, et enfin le groupe 3, groupe contrôle composé de sujets qui n'ont reçu aucune thérapie. L'effet consiste basiquement en ce que les moyennes sont différentes. Mais qu'est-ce qui est différent ? Est-ce le groupe 1 qui est différent du groupe 2 ? Ou bien le 1 est-il différent du 3 ? Ou encore le 2 est-il différent du 3 ?
1.1. Comparaisons par paires de groupes
Comme dans l'exemple précédent, on peut d'abord s'interroger sur les comparaisons de deux groupes que l'on peut faire au sein des k groupes. Ce qui peut en faire beaucoup. De manière générale, si nous avons k groupes, il y a k façons de choisir le premier groupe de la comparaison. Pour chaque groupe de départ, il reste alors k -1 façons de choisir le second groupe de la comparaison. cela ferait donc k *( k -1) façon de construire des comparaisons de deux groupes. Toutefois, dans ce calcul, on compte une comparaison pour le groupe 1 d'abord avec le groupe 3 en deuxième position, mais en on compte aussi une pour la comparaison ayant le groupe 3 comme premier groupe, et le groupe 1 comme second groupe. Or, la comparaison est la même dans ces deux cas. Il faut donc diviser par deux pour avoir le vrai nombre de comparaisons différentes possibles, soit k ×( k -1)/2. Ainsi avec k =3 groupes, cela fait 3×2/2 = 3 comparaisons par paires de groupes. Avec 4 groupes, cela fait 4×3/2 = 6 comparaisons. Avec 5 groupes, cela fait 5×4/2 = 10 comparaisons possibles. Etc.
1.2. Comparaisons par ensembles de groupes
Si nous reprenons notre exemple, on voit que l'on peut s'intéresser à comparer la thérapie A (groupe 1) avec la thérapie B (groupe 2) pour décider laquelle est la meilleure. On peut aussi comparer chacune d'elles avec le groupe contrôle. Mais on pourrait très bien décider de traiter ensemble les deux thérapies et les comparer au groupe contrôle. Autrement dit, de comparer les groupes 1 et 2 pris ensemble, contre le groupe 3. Ou encore 1 et 3 contre 2, etc.
Supposons que l'on travaille avec un facteur à quatre groupes, outre les six comparaisons par paire, il faudra encore considérer toutes les possibilités de comparer un groupe contre deux, mais aussi un groupe contre trois, et encore deux groupes contre trois.
4.2. Le problème du contrôle de l'erreur d'ensemble

Le nombre de comparaisons qu'il est possible de faire dépend de façon cruciale du nombre initial de groupes dans le facteur. Or, le nombre de comparaisons possibles augmente extrêmement vite avec le nombre initial de groupes dans le facteur.
En quoi est-ce un problème ? Tout simplement parce que l'on se donne conventionnellement une valeur seuil pour considérer qu'un test est significatif. Cette valeur seuil, habituellement 5%, signifie que dans 95% des cas on aura raison de conserver l'hypothèse nulle. Mais elle signifie aussi que dans 5% des cas où l'hypothèse nulle est vraie (ce que l'on ignore justement), on risque d'admettre une différence de moyennes comme significative alors qu'en fait l'écart n'était dû qu'au hasard. Si nous faisons cent tests dans un cas où l'hypothèse nulle est vraie, cinq de ces tests pourraient quand même suggérer que l'hypothèse nulle est fausse.
Or nous venons de voir que le nombre de comparaisons qu'il est possible de faire à partir des modalités d'un facteur expérimental croît très vite avec le nombre de ces modalités. Si donc nous gardons notre seuil de 5%, il suffit de faire toutes les comparaisons possibles, et nous aurons de bonnes chances d'en trouver de significatives par pur hasard. Si l'on ne prend garde à ce biais, les tests ne nous auront rien appris puisque c'est par pur hasard qu'ils auront été significatifs... alors que les procédures statistiques sont au départ justement conçues pour nous prémunir contre le risque d'avoir un résultat par hasard !
Il s'ensuit que les comparaisons internes aux groupes du facteur requièrent deux modifications par rapport aux comparaisons de moyennes vues jusqu'ici :
- On ne peut se contenter de calculer le taux d'erreur d'une comparaison individuelle comme si elle était seule, il faut minimiser le taux d'erreur de l'ensemble.
- On doit pouvoir agréger des ensembles de données avant de faire les calculs.
2.1. Passer du taux d'erreur d'une comparaison unique au taux d'erreur de l'ensemble des comparaisons
La procédure statistique standard suppose qu'on se donne arbitrairement un seuil d'acceptabilité du risque. Généralement on prend un seuil conventionnel, le plus souvent 5%, moins souvent 1%. Si la valeur p calculée à partir de nos données est inférieure à ce seuil, on juge acceptable le pari que l'hypothèse nulle est fausse. Il s'agit néanmoins toujours d'un pari et l'on peut perdre ! En fait, on dispose même d'une estimation de la probabilité de perdre : c'est précisément la valeur p !
Nous avons vu dans l'article précédent, que lorsque nous testons l'effet de facteurs présentant plus de deux groupes, le nombre de comparaisons qu'il est possible de faire entre les modalités de ces groupes peut être grand, en fonction du nombre de groupes opérationnalisant le facteur.
Admettons que nous prenions comme seuil d'acceptabilité la valeur classique de 5%. Pour chaque comparaison individuelle, nous admettions un risque de 5%. Mais puisqu'il y a de nombreuses comparaisons possibles, ces risques se cumulent et finalement, si nous avons de très nombreuses comparaisons, il devient presque certain que nous allons commettre au moins une erreur de type I alors même que pour chaque comparaison nous admettons un seuil de 5% seulement !
Nous allons donc, dans la suite de nos raisonnements, distinguer entre le taux d'erreur d'une comparaison individuelle et le taux d'erreur d'un ensemble de comparaisons. La probabilité de commettre au moins une erreur de type I dans un ensemble de comparaisons est appelée " Taux d'erreur de l'ensemble ". Si l'on est dans un cadre expérimental, on pourra aussi trouver l'expression "Taux d'erreur de l'expérience".
Idéalement, si l'on procède à plusieurs comparaisons, on veut que le taux d'erreur de l'ensemble des comparaisons reste en dessous de la barre des 5%. Chaque valeur p reste associée à une comparaison individuelle. Et l'on doit donc utiliser des procédures particulières pour maintenir le taux d'erreur de l'ensemble à un niveau suffisant pour corriger l'inflation du risque induite par la multiplication des comparaisons.
2.2. On doit pouvoir agréger des ensembles des données avant les calculs
Les procédures que nous avons étudiées jusqu'ici permettent de comparer soit deux groupes l'un avec l'autre, soit un ensemble de k groupes pris en bloc :
- Le test t nous permet de calculer le risque p pris en rejetant l'hypothèse nulle que m1 = m2 ,
- L'ANOVA, plus générale, nous permet de calculer le risque p pris en rejetant l'hypothèse nulle "omnibus" que m1 = m2 =... = mk-1 = mk .
Mais dans les comparaisons planifiées, en fonction de nos hypothèses théoriques, nous pouvons être amenés à opposer les sujets de deux groupes d'un côté, contre les sujets de trois autre groupes de l'autre. Par exemple, en étudiant le diagnostic médical, on compare trois groupes d'internes en médecine de spécialités différentes, contre deux groupes de médecins expérimentés, par exemple des pneumologues et des cardiologues. Ce n'est ni une comparaison à deux groupes, ni une comparaison globale. Que faire dans ce cas ? On aura donc envie de pouvoir regrouper les données des trois groupes d'un côté, des deux groupes de l'autre, puis de procéder à une comparaison de ces deux nouveaux ensembles. C'est ce que l'on appelle, "réaliser un contraste ".
Dans les pages et les articles suivant(e)s, nous allons étudier comment obtenir une valeur p pour les comparaisons individuelles telle que le taux d'erreur de l'ensemble sera maintenu à un niveau acceptable.
4.3. La correction de Bonferroni pour contrôler l'erreur de l'ensemble
Il existe une procédure générique qui fournit des résultats généralement considérés comme acceptables. Pour en comprendre la logique, commençons par exposer l’inégalité de Bonferroni.
3.1. L’inégalité de Bonferroni
L’inégalité de Bonferroni est un théorème selon lequel la probabilité d’une conjonction d’événements Ai ne peut jamais dépasser la somme des probabilités des événements conjoints :
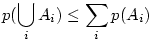
3.2. La correction de Bonferroni
Supposons que nous définissions un seuil maximum
c
, qui sera utilisé pour chacune de nos
k
comparaisons élémentaires. Puisque pour tout
i
,
 , l’inégalité de Bonferroni nous dit que le risque de l’ensemble des comparaisons (EC) est
, l’inégalité de Bonferroni nous dit que le risque de l’ensemble des comparaisons (EC) est
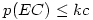
La difficulté que nous avons est que si nous opérons au moins 2 comparaisons avec un seuil de 0.05, rien n’empêche l'ensemble des comparaisons prises en bloc, "EC", d’avoir une probabilité d’erreur de type 1 supérieure au seuil de 0.5,
p
(EC)>.05, ce qui n’est pas acceptable. Il faut donc prendre un seuil maximum plus bas pour les comparaisons élémentaires. Notre problème est de trouver quelle valeur prendre.
Si l'on se donne 5% comme critère acceptable pour la significativité de l'ensemble, on peut écrire que 0.05 ≤
kc
, et donc 0.05/
k
≤ c
. Autrement dit, en prenant un seuil qui ne dépasse pas
c/k
pour les comparaisons élémentaires, on s'assure que le risque de la comparaison d'ensemble ne dépasse pas 0.05.
D’où le principe général de la correction de Bonferroni pour les comparaisons élémentaires : on applique notre test, quel qu’il soit (t
de Student, ANOVA, etc…) mais on se donne un seuil de significativité pour chaque comparaison qui soit directement dépendant du nombre global de comparaisons.
Il faut noter que
cette méthode s’applique à toutes les comparaisons, et en particulier aux comparaisons planifiées (contrastes) comme aux comparaisons post-hoc. Nous verrons des exemples spécifiques dans les articles en question.
3.3. La variante de Dunn-Šidák
Il s'agit d'une légère variante du test de Bonferroni qui peut offrir un très très léger gain de la capacité à obtenir un test significatif lorsque l'hypothèse nulle est fausse (i.e, un très léger gain de puissance statistique). Le principe est le même mais on utilise l'inégalité
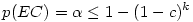
qui permet de garder l'erreur d'ensemble (EC) à un niveau inférieur au seuil α si on teste chacune des k comparaisons élémentaires au seuil
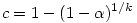
La table ci-dessous compare les seuils de signification des comparaisons élémentaires corrigés par Bonferroni et par Dunn-Šidák, afin de maintenir l'erreur de l'ensemble à un niveau .05. L'écart est minime ! De plus, le gain qu'on peut attendre décroît avec le nombre de comparaisons, et il est insignifiant quel que soit le nombre k de comparaisons si l'on veut maintenir l'erreur de l'ensemble à un niveau .01.
4.4. Primauté de l'ANOVA globale?
Mais avant de rentrer dans les détails de ces techniques, dans les articles suivants, une question d'importance doit être traitée : peut-on procéder aux comparaisons "locales" entre groupes du facteur, si l'ANOVA globale n'est pas significative ?
4.1 Qu'est-ce qui prime, le test global (l'ANOVA "omnibus") ou bien les comparaisons spécifiques entre les différents groupes du facteur ?
Si l'ANOVA globale est significative, cela signifie qu'on a mis en évidence un effet et donc il est évidemment légitime de s'interroger sur la nature de cet effet. Il y a de nombreuses façons de procéder pour répondre à une telle question, mais en restant niveau statistique on peut déjà s'interroger sur les groupes qui sont porteurs des différences significatives.
Donc en fait la question de la préséance de l'ANOVA globale revient à savoir s'il faut ou non procéder aux comparaisons détaillées lorsque l'ANOVA globale n'est PAS significative ?
En ce cas, l'usage traditionnel est de ne pas aller plus loin. Toutefois on peut quand même s'interroger sur les comparaisons entre groupes.
Howell (2008), par exemple, argumente qu'il n'y a aucune vraie raison de se limiter à travailler sur des cas où l'ANOVA globale est significative. En effet, certaines procédures utilisées actuellement pour les comparaisons multiples ne sont même pas spécifiquement attachées à l'ANOVA et peuvent s'utiliser dès lors que l'on a des comparaisons multiples à faire. De plus, l'exigence de significativité rend les tests utilisés conservateurs, c'est-à-dire qu'ils ont alors tendance à devenir trop exigeants.
Mon conseil cependant, si vous ne voulez pas vous exposer aux critiques en réalisant ce type de tests alors que l'ANOVA globale n'est pas significative est de vous réfugier derrière l'autorité et de bien préciser explicitement qu'un auteur de référence comme Howell, l'autorise.
4.2. Mais faut-il rapporter l'ANOVA globale ?
On peut alors se demander si l'on a encore besoin du test global et s'il faut s'embêter à le rapporter. Les logiciels actuels le donnant sans effort, cela ne coûte rien de le faire donc ne prenez pas de risque inutile : rapportez systématiquement la comparaison globale en attendant le jour éventuel où l'usage aura changé.
4.5. Distinguer les comparaisons "planifiées" et "post-hoc"
Face au problème principal de ce chapitre, la nécessité de contrôler l'erreur d'ensemble, l'usage traditionnel est de distinguer deux types de comparaisons, les comparaisons "a priori" et "a posteriori", ces dernières étant plus courament qualifiées de "post-hoc".
Les comparaisons planifiées ou "a priori" sont les comparaisons que l'on avait projeté de faire avant même d'avoir connaissance des résultats statistiques globaux. Ce sont des comparaisons qui ne sont pas motivées par une observation de données en cours de traitement, mais par une analyse préalable de la situation. On ne peut donc pas leur reprocher de figurer dans les résultats parce que l'on a profité du hasard car elles correspondent en fait à des hypothèses théoriques.
Les comparaisons "post-hoc" ou "a posteriori" au contraire, sont celles qui ne sont pas motivées par des considérations théoriques mais tout simplement par une approche exploratoire des données : on regarde tout ce qui pourrait être significatif. Comme l'exploration mobilise potentiellement l'ensemble de toutes les comparaisons possibles, ce sont surtout ces dernières qui sont sensibles à l'effet de capitalisation sur la chance.
5. Comparaisons planifiées dans l'ANOVA : contrastes
Objectifs. Montrer quand et comment tester des hypothèses décidées avant les analyses et concernant deux ou plusieurs des groupes qui opérationnalisent les modalités du facteur expérimental. Introduire la notion de contraste, orthogonal ou non.
Prérequis.
- Cours de L1
- Approche intuitive de l'inférence statistique
- Hypothèse nulle
- Principe général de la comparaison de moyennes
- t de Student
- ANOVA à 1 facteur
Résumé. Un contraste est la création, à partir des groupes qui opérationnalisent un facteur, d'une comparaison où l'hypothèse nulle est m1 = m2. Cette création consiste à répartir les groupes en trois ensembles : (1) les groupes dont les données vont servir à construire la moyenne m1 ; (2) ceux qui vont participer à construire la moyenne m2 ; et enfin (3) ceux qui ne participent pas à la comparaison.
5.1. Notion de contraste
1.1. Opposer ou exclure les groupes

Généralement, on réalise les comparaisons planifiées au moyen d'une analyse par contraste. Comme le nom l'indique, un contraste revient à mettre en opposition deux ensembles de données. Souvent, une troisième opération est aussi réalisée qui consiste à exclure un troisième ensemble de données.
La construction d'un contraste est la création, à partir des groupes qui opérationnalisent un facteur, d'une comparaison où l'hypothèse nulle est m1 = m2 . Cette création consiste à répartir les groupes en trois ensembles : (1) les groupes dont les données vont servir à construire la moyenne m1 ; (2) ceux qui vont participer à construire la moyenne m2 ; et enfin (3) ceux qui ne participent pas à la comparaison.
De ce fait, la question du contraste revient à définir ce qui ira d'un côté, ce qui ira de l'autre côté, et ce qui n'allant nulle part, se trouvera exclu de la comparaison. Pour ce faire, nous définirons un contraste comme un jeu de coefficients qui affecteront chacun des groupes de l'ANOVA omnibus. Par exemple, s'il y a cinq groupes, un contraste sera un jeu de cinq coefficients.
La question devient alors de bien choisir les coefficients pour permettre la partition des groupes en trois ensembles telle qu'évoquée plus haut.
1.2. Construire le contraste
Notre problème est de construire les moyennes m1 et m2 à partir des moyennes des groupes de l'ANOVA. Pour cela, nous allons donc attribuer des coefficients à chacune des moyennes issues des groupes de données.
Une somme pondérée est un nombre que l'on calcule à partir d'un ensemble de valeurs auxquelles on attribue des coefficients. On fait ensuite la somme de tous les produits coefficient × valeur.
Si la somme de tous les coefficients en jeu dans la somme pondérée fait 1, on parlera de moyenne pondérée. Pour obtenir une somme pondérée à partir de n'importe quel jeu de coefficients dont au moins l'un est non nul, il suffit de diviser le résultat de la somme pondérée par la somme de tous les coefficients. Si en plus tous les coefficients sont égaux, nous aurons une moyenne ordinaire. Donc pour constituer les agrégats donnant m1 et m2, il suffira de bien choisir les coefficients.
Pour exclure un groupe, il suffira d'affecter à sa moyenne un coefficient nul.
Par ailleurs, si nous avons m1 =m2, cela revient à dire que m1 - m2 = 0, ou encore que m2 - m1 = 0.
En résumé, on voit donc qu'on peut facilement construire la comparaison de la façon suivante :
- Tous les groupes qui seront exclus de la comparaison recevront un coefficient nul
- Tous les groupes inclus d'un même côté de la comparaison (i.e., qui s'agrégeront pour former m1) recevront un coefficient positif tandis que les groupes inclus, mais qui vont de l'autre côté (i.e., qui s'agrégeront pour former m2) recevront un coefficient négatif.
Par exemple, supposons que nous ayons 5 groupes, dont les moyennes respectives sont, faisons simple, 11, 12, 13, 14 et 15. Supposons aussi que nous voulions mettre ensemble les groupes 1 et 4, les opposer aux groupes 3 et 5, et exclure le groupe 2, nous donnerions un coefficient positif aux groupes 1 et 4, un coefficient négatif aux groupes 3 et 5, et un coefficient nul au groupe 2. Ainsi, nous pourrions choisir pour le contraste la séquence de 5 valeurs suivantes, dans laquelle la première valeur représente le coefficient du groupe 1, la deuxième valeur le coefficient du groupe 2, etc.
(1;0;-1;1;-1)
Dans ce qui suit, on expose la construction des deux termes m1 et m2 à des fins de compréhension de ce qu'est un contraste. En réalité, lorsque l'on teste un contraste on ne s'embête généralement pas à calculer ces moyennes : une fois qu'on a défini les coefficients, le logiciel réalise tous les calculs pour nous !
Pour construire l'agrégation m1, on somme tous les produits impliquant un coefficient strictement positif (i.e., > 0)
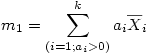
Autrement dit, nous aurons m1 = (1×11)+(1×14)=25
Pour construire l'agrégation "- m2", on somme tous les produits impliquant un coefficient strictement négatif (i.e., < 0).
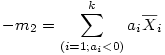
Donc, nous aurons ici -m2 = (-1×13)+(-1×15) = -28, soit encore m2 = +28.
Le signe choisi importe peu, car en réalité le contraste est la somme m 1 + (-m 2 ). En sommant ces deux agrégats, nous pratiquons en réalité une différence m1-m 2. Cette différence sera comparée à la valeur de référence 0, réalisant ainsi notre hypothèse nulle m1 -m2 =0 !
Sommer m1 et -m2 revient tout simplement à réécrire en une seule les deux sommes précédentes. Ce n'est même pas la peine de préciser la condition ai ≠0 pour ne pas prendre en compte les groupes exclus de la comparaison puisque leurs coefficients étant nuls, les produits associés le seront aussi ! Nous dénoterons par la lettre Ψ le contraste ainsi obtenu et donc
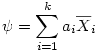
Enfin, il faut savoir que les logiciels comme SPSS ou Statistica disposent d'outils d'aide à la construction de contrastes orthogonaux comme options associées aux ANOVA.
Nous examinerons à la page suivante comment tester statistiquement cette hypothèse nulle, mais pour l'instant continuons à développer l'idée de contraste.
1.2. Le contraste comme généralisation de la comparaison de deux groupes
D'un certain point de vue, on peut remarquer que si l'on a k groupes, que l'on met un coefficient, disons de 1 à un groupe, de -1 à un autre groupe, et 0 à tous les autres groupes, nous nous trouvons en fait à réaliser une simple comparaison de moyennes à deux groupes, rien de plus qu'un simple test t de Student ou, ce qui revient au même une ANOVA à deux groupes. Ainsi, tester le contraste
(1;0;-1;0;0)
revient tout simplement à faire un test de Student entre les données des groupes 1 et 3 !
5.2. Quels coefficients choisir ?

Bien qu'extrêmement libre, le choix des coefficients ne se fait tout de même pas au hasard car certaines contraintes devraient être respectées.
En particulier il faut équilibrer les deux côtés de la comparaison, ce qui se traduit par le fait que la somme des coefficients soit nulle.
2.1. Nullité de la somme des coefficients
Les coefficients vont déterminer le poids de chaque groupe dans la comparaison. La seule vraie contrainte que nous ayons pour que l'on puisse parler de contraste est la nullité de la somme des coefficients :il faut que la somme des coefficients positifs soit égale à la somme des coefficients négatifs. Brauer et McClelland (2005) parlent alors de "contraste centré".
En reprenant l'exemple précédent nous pourrions noter notre contraste
(2;0;-2;2;-2)
et le résultat serait exactement le même. Ou encore
(-0.5;0;0.5;0;-0.5;0.5)
2.2. Comment affecter les poids des groupes à l'intérieur d'un des deux agrégats ?
2.1.1. Le cas standard (effectifs équilibrés)
Imaginons que nous ayons à comparer cinq groupes, deux d'un côté, trois de l'autre. Nous ne pouvons évidemment pas donner les mêmes valeurs absolues aux coefficients positifs et négatifs sinon nous ne pourrons pas avoir une somme nulle des coefficients puisque justement nous n'avons pas le même nombre de coefficients négatifs et positifs.
Une solution consiste à prendre comme valeur absolue l'inverse du nombre de groupes à agréger. Du côté où l'on a deux groupes, nous donnerons donc 1/2 et 1/2. Du côté où l'on a trois groupes cela donnera 1/3; 1/3; 1/3. Il ne reste alors qu'à attribuer un signe (arbitrairement) à l'un des deux blocs de coefficients et le tour est joué. On aura ainsi par exemple
(-0.5;033;0.33;-0.5;0.33)
Cela dit ce n'est pas très élégant et en outre on perd un centième lors de la sommation des arrondis. On peut alors tout multiplier par 3 pour avoir des valeurs sans arrondis :
(-1.5;1;1;-1.5;1)
Si l'on veut se débarrasser complètement des décimales, on peut encore tout multiplier par 2 :
(-3;2;2;-3;2)
Ces trois jeux de coefficients donneront exactement le même résultat statistique, mais la dernière version sera peut-être plus facile à manipuler.
Remarquons qu'on pouvait obtenir directement ce résultat avec une règle consistant à attribuer comme coefficients aux éléments d'un agrégat, le nombre d'éléments de l'autre agrégat. Ici on contraste 2 groupes contre trois, donc on met 3 aux deux groupes du premier agrégat et 2 aux trois groupes du deuxième agrégat. Il ne reste alors qu'à attribuer un signe "-", toujours arbitrairement, à l'un des deux blocs de coefficients.
2.1.2. Les effectifs déséquilibrés
Techniquement, c'est le cas lorsque les effectifs entre les groupes sont différents. Toutefois, lorsque les différences d'effectifs sont imputables aux seules fluctuations aléatoires d'échantillonnage (comme lorsque l'on perd quelques données dans chaque groupe, mais pas la même quantité), on peut, selon Howell, se rabattre sur le calcul précédent, ce qui revient fondamentalement à donner le même poids à toutes les moyennes, même si elles sont issues d'effectifs différents.
Lorsqu'au contraire les différences d'effectifs traduisent une réalité (par exemple si on mène une expérience dans un milieu où existe une grande majorité de femmes, le plus grand nombre de femmes dans les échantillons ne doit rien au hasard) et que donc on souhaite donner plus de poids aux moyennes des groupes représentant une part plus importante de la population globale, on peut calculer la moyenne pondérée par les effectifs.
Pour ce faire, chaque groupe à inclure dans l'un des deux agrégats (les autres garderont un coefficient nul quel que soit leur effectif) recevra un coefficient dont la valeur sera le rapport entre son effectif et l'effectif global de l'agrégat. Par exemple si on contraste trois groupes d'effectifs 7, 8 et 9 contre deux groupes d'effectifs 8 et 10, les trois premiers recevront les coefficient 7/(7+8+9); 8/(7+8+9); et 9/(7+8+9). Les deux derniers groupes recevront les coefficients 8/(8+10) et 10/(8+10). Bien sûr, il faudra choisir de négativer les coefficients de l'un des deux agrégats.
Voyons maintenant comment tester la significativité du contraste.
5.3. Le test statistique du contraste
On peut passer soit par un test du F soit par un test du t de Student mais dans les deux cas la formule utilisée passe par le calcul du carré moyen du contraste.
3.1. Remarque préliminaire importante
Les tests qui suivent sont déterminés pour un contraste particulier. Lorsque plusieurs hypothèses cibles permettent de planifier plusieurs contrastes, il faut limiter l'erreur de l'ensemble des comparaisons cibles (voir l'article sur les comparaisons multiples et plus particulièrement la page sur la correction de Bonferroni). Ce qui, nous l'avons vu, suppose de se donner un critère plus sévère pour chaque comparaison.
Rappelons que si l'on se donne α comme critère acceptable pour la significativité de l'ensemble EC des k comparaisons cibles (ici les contrastes), on se donnera comme critère pour chaque contraste élémentaire :
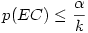
3.1. Calcul du carré moyen du contraste
Un contraste n'a qu'un seul degré de liberté puisque c'est une comparaison entre deux agrégats (et donc 2-1=1 ddl), Et puisque le carré moyen est la somme des carrés divisée par le nombre de degrés de liberté, le CM d'un contraste est en réalité égal à sa somme des carrés. C'est cette dernière qu'il nous faut calculer.
Cette somme ne dépend que des moyennes des groupes à agréger, des coefficients choisis, et des effectifs.
Nous avions vu que le contraste Ψ est facile à calculer comme une simple somme pondérée à partir des moyennes des groupes pris en compte et des coefficients choisis
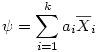
L'on a alors dans le cas général :

qui dans le cas d'effectifs équilibrés (tous les n1 = n2 = ... = n ) se simplifie en

3.2. Test statistique du contraste
3.2.1. par le
F
de Fisher
Le test est facile à réaliser à la main. Il s'agit de traiter le contraste comme un facteur à deux groupes dans une ANOVA, calculer le F de Fisher et la valeur p associée selon la méthode habituelle, à savoir
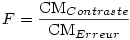
Si les deux agrégats comprennent n sujets, les degrés de liberté seront donc 1, puisqu'il y a deux agrégats, et n -1 pour les degrés de liberté de l'erreur.
Le calcul du carré moyen de l'erreur est simplissime puisque c'est tout simplement le même que celui de l'ANOVA globale ! Donc nous ne reviendrons pas dessus.
3.2.1. par le t de Student
On trouve aussi dans les logiciels de statistique un test par le t de student. Mais ici la valeur de t peut s'obtenir en prenant la racine carré du F puisque dans le cas particulier où il n'y a que deux groupes (ou deux agrégats dans le cas d'un contraste), F = t ²
Voyons maintenant la notion de contrastes orthogonaux.
5.4. Les contrastes orthogonaux
4.1. La question : comment rendre compte des variations expliquées par le facteur ?
Jusqu’ici, nous avons travaillé sur des contrastes élémentaires, c’est-à-dire que nous n’avons envisagé qu’un seul contraste à la fois. Mais rien qu’à partir d’un ensemble de 3 groupes, on peut construire trois comparaisons de deux groupes, et trois comparaisons opposant l’agrégation de deux des groupes au troisième. Avec quatre groupes, on peut faire des comparaisons 1 contre 3, 1 contre 2, 1 contre 1, 2 contre 2 ! Etc. les possibilités augmentent très vite avec le nombre de groupes. Et avec le nombre de comparaisons, le risque de commettre une erreur de type I quelque part (rejeter à tort l’hypothèse nulle) augmente dangereusement puisque chaque comparaison sera porteuse d’une part de risque supplémentaire.
La question qui se pose alors est de trouver les comparaisons qui sont pertinentes d’un point de vue théorique et qui, idéalement, devraient capturer l’essentiel des variations que l’on sait expliquer, c’est-à-dire les variations représentées par la somme des carrés du facteur. On va donc chercher à trouver un ensemble de contrastes qui, à eux tous, capturent l’ensemble des variations expliquées, ni plus ni moins.
4.2. Notion de comparaisons indépendantes
Pour traiter cette question, on va chercher à mobiliser des comparaisons indépendantes, de façon à ce que chaque comparaison explique des variations qui ne sont pas celles qui sont déjà expliquées par d’autres comparaisons. Deux contrastes indépendants sont dits « orthogonaux ». En effet, en géométrie, deux axes sont « orthogonaux » s’ils font un angle droit. Le fait qu’ils soient orthogonaux traduit une indépendance des coordonnées des points qui se trouvent sur l’une et l’autre puisque tout mouvement sur un axe laisse inchangé la coordonnée sur l’autre axe (monter ou descendre dans un ascenseur ne modifie aucunement ma position au sol).
On peut assimiler les contrastes à des vecteurs de k coefficients (un coefficient par groupe du facteur). Or, en géométrie, deux vecteurs dits sont orthogonaux si la somme des produits de leurs coordonnées prises deux à deux est nulle (la coordonnée x 1 est multipliée avec la coordonnée x2, on y ajoute le produit de la coordonnée y1 avec la coordonnée y2 , etc. C’est ce que l’on appelle le produit scalaire. Donc, ici, nous dirons que :
Deux contrastes sont orthogonaux si la somme des produits de leurs coefficients est nulle.
Voici un exemple de deux contrastes orthogonaux construits avec trois groupes.
(1 0 -1) et (-1 2 -1) : le produit scalaire donne 1*-1 + 0*2 + -1*-1 = 0
4.3. Ensemble de contrastes orthogonaux
Rappelons que nous voulons représenter toute la variance expliquée par le facteur. Le facteur ayant k groupes, il a k -1 degrés de liberté. Et comme un contraste n’a qu’un degré de liberté, il faudra exactement k -1 contrastes orthogonaux deux à deux pour rendre compte de l’ensemble de la variance expliquée par le facteur.
Si l’on dispose d’un ensemble de k -1 contrastes orthogonaux, alors on a la propriété
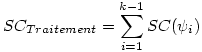
Brauer et McClelland (2005) argumentent que lorsque l’on dispose d'hypothèses a priori, plutôt que d’utiliser l’ANOVA omnibus, il faudrait travailler avec des contrastes, en s’assurant,
1. que le(s) contraste(s) cible(s) capture(nt) une part significative de la variance (ce qu’on voulait capturer est significatif)
2. que la variance intergroupe résiduelle est non significative (ce que l’on ne capture pas n’est pas important)
Concrètement, cela revient à définir le (ou les) contraste(s) cible(s) sur la base d’une analyse théorique,construire le jeu des contrastes orthogonaux supplémentaires requis pour atteindre le bon nombre de degrés de liberté (k-1 en tout), puis introduire tout cela dans une analyse globale. On peut le faire à la main, mais nous supposerons qu’un logiciel de statistiques est disponible.
On vérifie alors que les contraste(s) cibles et eux seuls sont significatifs.
6. Comparaisons non planifiées : tests post-hoc
Objectifs. Montrer quand et comment comparer les moyennes des différents groupes qui opérationnalisent les modalités du facteur expérimental, alors que l'on ne disposait pas d'hypothèse à ce sujet avant de voir les données.
Prérequis.
- Cours de L1
- Approche intuitive de l'inférence statistique
- Hypothèse nulle
- Principe général de la comparaison de moyennes
- t de Student
- ANOVA à 1 facteur
- Le problème du contrôle de l'erreur d'ensemble
Résumé. Un test post-hoc est une procédure qui permet de comparer des groupes sans qu'une hypothèse sur la relation entre ces groupes ait été posée avant d'examiner les données. Mais la multiplication des comparaisons augmente le risque de commettre sur l'ensemble des comparaisons au moins une erreur de type I (rejeter à tort l'hypothèse nulle). Une série de procédures de tests classiques est proposée : LSD, Student-Newman-Keuls, Tukey, REGWQ, Scheffé... Ces tests permettent -- avec plus ou moins de succès selon les cas -- de gérer l'inévitable compromis entre la nécessité de conserver suffisamment faible le risque de rejeter l'hypothèse nulle lorsqu'elle est vraie, et la nécessité de conserver une puissance statistique suffisante pour rejeter l'hypothèse nulle lorsqu'elle est fausse.
6.1. Notions de base sur les tests post-hoc
1.1 Pourquoi des tests a posteriori ?
Précédemment, nous avons examiné le cas des
comparaisons planifiées. Mais lors de l’analyse des données, l’examen des résultats suscite des hypothèses réellement intéressantes à tester, mais auxquelles on n’avait pas pensé avant de voir les données. Traiter ces dernières comme des hypothèses a priori serait illégitime, car cela reviendrait à « capitaliser sur la chance ». À moins bien sûr de procéder d’abord à un nouveau recueil de données, de sorte que l’hypothèse ne provienne pas des données sur lesquelles on la teste ! Dans ce dernier cas, on peut tester l’hypothèse en question avec une comparaison planifiée sur le deuxième recueil de données, mais pas sur le premier).
Une autre situation fréquente est le besoin de tester de manière exploratoire toutes les possibilités de différences significatives entre groupes de données.
1.2 Ce que sont les tests post-hoc
Les tests post-hoc, ou « a posteriori » ne présupposent pas l’existence d’une hypothèse expérimentale préalablement définie.
Les procédures existantes sont nombreuses et les différents logiciels de statistique facilement accessibles aux psychologues (payants comme SPSS, Statistica, SAS, ou gratuits comme jamovi ou R), en proposent de nombreuses. Se pose la question du choix de la procédure à utiliser.
1.3 Le problème de la puissance statistique
On pourrait avoir envie de tester les différences de moyennes au sein de chaque paire possible d’échantillons avec des tests
t, en appliquant la
correction de Bonferroni. Après tout, cette dernière ne suppose pas d’avoir une hypothèse a priori et donc il n’existe pas d’objection formelle à son utilisation. Ce peut être un test post-hoc comme un autre. Mais on le réserve habituellement aux comparaisons planifiées, car ce test devient rapidement trop exigeant au fur et à mesure qu’augmente le nombre de comparaisons possibles.
La capacité d’un test à rejeter l’hypothèse lorsqu’elle est fausse est appelée la
puissance statistique
du test. En effet, admettons que l’hypothèse nulle soit fausse : pour une différence de moyennes donnée, et pour un certain niveau de bruit (la variance des échantillons), il faudra obligatoirement un certain nombre de sujets pour qu’un test devienne capable de détecter la différence significative. Certains tests sont peu puissants, d’autres sont plus puissants (requièrent moins de sujets). C’est pourquoi d’autres procédures ont été développées, les tests post-hoc. Ces procédures sont généralement plus « puissantes », c’est-à-dire plus facilement capables de détecter une différence significative. Ou pour le dire autrement, ces procédures requièrent moins d’observations pour qu’une même différence de moyenne atteigne le seuil de significativité.
En revanche, leur multiplicité ouvre la question du choix du test post-hoc à utiliser, et des critères que l’on peut se donner pour choisir.
1.4 Choisir un test « laxiste », « conservateur », ou entre les deux ?
Pour choisir parmi les procédures de test qui existent, le premier critère qui vient à l’esprit est celui de la puissance statistique. En effet, les différents tests ne sont pas équivalents à cet égard. Certains donneront plus facilement une valeur significative et seront qualifiés de laxistes. D’autres au contraire donneront difficilement un résultat significatif et seront qualifiés de plus « conservateurs ».
Il n’existe pas de règle stricte et consensuelle pour guider le choix dès lors que les conditions d’application de chaque test sont respectées.
C’est pourquoi mon conseil serait de vous appuyer sur ce que vous voulez montrer et choisir ce qui vous donnera l’argument le plus robuste.
- Si vous voulez montrer qu’il existe une différence significative, alors pouvoir exhiber une différence significative obtenue malgré l’utilisation d’un test conservateur est plus convaincant pour les lecteurs.
- Au contraire, vous souhaiterez parfois montrer que deux groupes ne sont pas différents. Légalement, on ne peut jamais affirmer une telle chose à moins d’utiliser des procédures spécifiques (méthodes bayésiennes comme l’inférence « fiducière » notamment) qui ne sont pas du niveau de ce cours. Affirmer que l’hypothèse nulle est vraie (qu’il n’y a pas de différence entre les groupes) revient à commettre une erreur de débutant, ce que dans le jargon des chercheurs on appelle parfois « conclure sur une hypothèse nulle ». Même si l’on ne peut pas affirmer formellement l’égalité, il est tout de même parfois appréciable de pouvoir montrer qu’à tout le moins on ne détecte pas de différence significative. Et votre argument sera alors plus convaincant si vous avez choisi un test laxiste puisqu’il était justement le plus à même de fournir une valeur significative. Surtout si vous avez pris soin d’avoir suffisamment de participants pour que le manque de significativité ne puisse pas être attribué à un trop faible effectif.
Nous allons maintenant brièvement examiner quelques tests présents dans les logiciels de statistique, en les classant du plus laxiste au plus conservateur. Nous présenterons d'abord les tests usuels de comparaisons par paires de moyennes, pour nous examinerons deux tests qui fonctionnement différemment, un test permettant d'examiner des contrastes (donc de comparer des agrégations de plusieurs moyennes) en post-hoc, et un test permettant de donner un statut particulier à un groupe censé être différent des autres (appelé groupe "contrôle" ou groupe "témoin").
6.2. Les données pour les exemples
Dans cette page nous présentons les données qui serviront pour les exemples numériques de tests post-hoc. Les traitements informatisés sont réalisés ici avec le logiciel SPSS (PASW 18).
Il s'agit de données entièrement fictives. Pour faciliter la lecture, nous les présentons sous forme de 5 colonnes intitulées VD1 à VD5. Dans la réalité des tests statistiques, il s'agira d'une seule colonne VD, et c'est une autre colonne intitulée VI qui signalera au logiciel dans quel groupe de participants la mesure a été prise. Voici donc les données brutes :
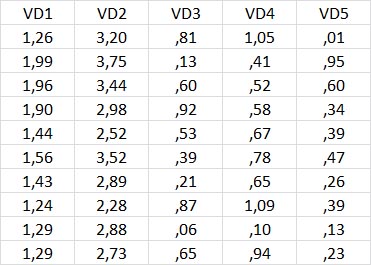
Sans être parfaites, ces données sont à peu près normales au sens où les paramètres d'asymétrie et d'aplatissement sont suffisamment correctes pour l'exemple. Voici un graphique de statistiques descriptives qui résume ces données :
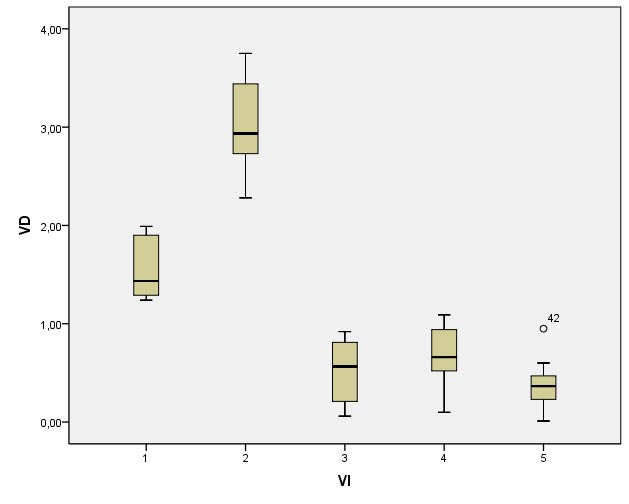
Et voici les statistiques descriptives pour les différents groupes :
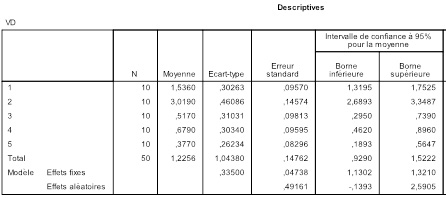
Les effectifs sont équilibrés puisqu'il y a exactement 10 participants par groupe. Par ailleurs, le test de Levene montre que les variances peuvent être considérées comme homogènes, puisque le test n'est pas significatif :
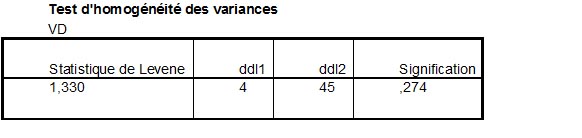
6.3. Les tests par paires
Les méthodes de test sont proposées ici par ordre du plus laxiste au plus conservateur.
Bien entendu, nous avons commencé par réaliser une ANOVA à un facteur sur ces données. Il se trouve que l'ANOVA globale est largement significative mais ce n'est pas une nécessité pour tous les tests que nous allons voir :
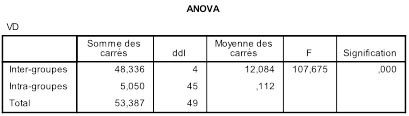
3.1 Le test de la plus petite différence significative (LSD) de Fisher
3.1.1. Idée générale du test
Le plus laxiste des tests post-hoc est le test de Fisher dit LSD (pour Least Square différence).
La « différence des moindres carrés » est en fait tout simplement la différence des moyennes des deux groupes, comme dans n’importe quel test
t. De fait, ce test consiste à calculer un
t
de Student. Rappelons que ce dernier consiste basiquement à diviser une différence de moyennes par l’erreur standard de l’échantillon virtuel composé des deux groupes à comparer (voir
l’article ici).
L’idée du test LSD de Fisher est de réaliser un test
t
de la même façon que d’habitude, mais avec un niveau de bruit qui n’est pas limité aux variations internes aux deux groupes cibles. Au contraire, il intégrera l’ensemble des bruits de tous les groupes. Pour ce faire, on prendra à la place de l’erreur standard de l’échantillon virtuel (celui construit par agrégation des deux échantillons à comparer) la racine carrée du carré moyen de l’erreur dans l’ANOVA.
L’erreur standard, rappelons-le, n’est autre qu’une sorte d’écart-type normalisé par la taille de l’échantillon, puisqu’il s’agit de la racine carrée de la variance divisée par la racine carrée de l’effectif. Mais cette normalisation est ici limitée par le fait qu’on la calcule en calculant l’écart-type à partir de l’effectif de l’échantillon virtuel (la somme des effectifs des deux groupes) et non à partir de l’effectif global qui a servi à générer la mesure des variations !
Si n est le nombre total de sujets (50 dans l'exemple), et k le nombre de groupes (5 dans l'exemple), Mi et Mj les moyennes de deux groupes à comparer de manière post-hoc, beaucoup de ces tests font usage d’un calcul du test t de Student, avec n-k degrés de libertés calculé par la formule suivante pour groupes équilibrés (les groupes sont de tailles égales, ce qui est le cas ici) :
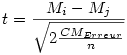
Nous pouvons repérer directement le CMErreur dans le tableau d'ANOVA à la ligne intra-groupes : 0,112. Attention, il sera utilisé pour la plupart des tests post-hoc que nous verrons.
3.1.2. Application numérique
Voici les résultats que donne SPSS sur notre exemple :
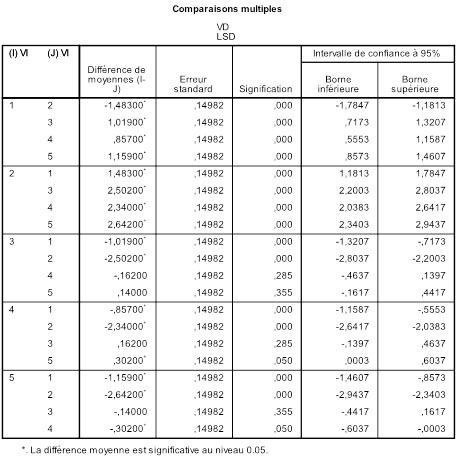
Vous voyez que toutes les comparaisons par paires possibles sont explorées. Si nous prenons par exemple le sous-tableau des comparaisons impliquant la moyenne M1, nous voyons qu'il y a une ligne par moyenne comparée avec M1. La première ligne compare M1 et M2.
Pour notre exemple, nous prendrons i =1 et j =2. La différence des moyennes est (voir le tableau des moyennes par groupes à la page précédente)
M1 - M2. = 1.536 - 3.019 = -1.483
Le t s'obtient en divisant la différence des moyennes par l'erreur standard intra-groupes, laquelle s'obtient dans le cas présent (groupes équilibrés, variances homogènes) par la formule suivante :
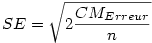
où n est le nombre de sujets par groupe. Ce qui donne
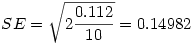
Vous remarquerez que l'erreur standard ne change pas quelle que soit la paire de groupes que l'on considère. C'est normal puisqu'on la calcule une fois pour toutes sur la base du carré moyen de l'erreur dans l'ANOVA. Par contre, le t change avec les paires. Ici, on a t =-1.483/0.14982 = -9.899. Cette valeur est largement significative, au point que la valeur p présentée dans le tableau de résultats, quoique non nulle, est tronquée à p=.000.
Le t que nous venons de calculer ne figure pas explicitement dans le tableau. Nous pouvons néanmoins utiliser la ligne 4 du sous groupe 3 qui, n'étant pas significative, nous donne une valeur p plus exploitable pour vérifier nos formules. L'erreur standard est la même et la différence de moyenne est -.162. D'où un t =-.162/0.14982=-1.081. Nous testons cette valeur t avec N - k =50-5=45 degrés de libertés. En utilisant une formule de tableur (Sous Excel par exemple "=LOI.STUDENT.BILATERALE(ABS( t ); ddl )", en remplaçant t par sa valeur et ddl par 45), et après arrondi, nous obtenons effectivement la valeur p =.2853.
Bien entendu, le test est bilatéral puisque post-hoc et que donc nous n'avions pas d'hypothèse. Notez dans la formule la fonction "abs", valeur absolue, rendue obligatoire par le fait que le t peut être de signe négatif, ce qui est d'ailleurs le cas ici.
3.1.3 Pourquoi le LSD est-il "laxiste" ?
Tout simplement parce que les valeurs
p
sont calculées exactement comme d’habitude, sans véritable protection contre l'augmentation du risque au niveau de l'ensemble des comparaisons ! La conséquence est que le taux d’erreur de l’ensemble va tendre à excéder le seuil de .05, et ce d’autant plus qu’on a de groupes en jeu. Selon Howell, et pour des raisons qui seraient trop complexes à développer ici, il existe tout de même un cas où il est légitime, et même recommandé :
• Si l’ANOVA globale est significative ET
• s’il n’y a que trois groupes en jeu.
Dans les autres configurations, ce test est à éviter.
3.2 Le test Student-Newman-Keuls
Le test Student de Newman-Keuls s’appuie sur la statistique
q
dite «
statistique d’écart studentisée
» qui s’obtient sur la base d’un classement des moyennes comparées de la plus petite à la plus grande. On lit la significativité de
q
à partir d’une distribution d’échantillonnage (ou on compare
q
aux valeurs critiques données par une
table de la statistique q) avec pour paramètres le nombre
r
d’échelons d’écart entre les groupes comparés (pour en savoir plus, voir l’article spécifique) et le nombre de degrés de libertés de l’erreur dans l’ANOVA.
Par exemple, s’il y a cinq groupes, et qu’après rangement des moyennes
M1, la plus petite, à
M5, la plus grande, et qu’on compare
M3
et
M4, on prendra
r
=1 pour entrer dans la table de
q.
Quoiqu'encore utilisé, ce test est maintenant de plus en plus déconseillé, car le risque de commettre au moins une erreur au niveau de l’ensemble des comparaisons augmente presque linéairement avec le nombre de paires de moyennes à comparer.
3.3 Le test de la différence vraiment significative de Tukey
Le test HSD de Tukey, test de la différence vraiment significative (HSD signifie « Honestly Significant difference ») s’appuie comme le précédent sur la
statistique d’écart studentisée
q.
Pour le test HSD de Tukey, toutefois, on fait comme si TOUTES les comparaisons avaient le nombre maximum d’échelons possibles. Ainsi, même si l’on compare les moyennes
M3
et
M4
parmi 6, on calculera la significativité de
q
à partir de
r
=6 et non à partir de
r
=2.
Contrairement au LSD, qui est trop laxiste, le HSD est conservateur puisqu’il traite tous les cas comme si c’était le pire.
Le test HSD teste l’hypothèse nulle globale et suppose que les données soient normalement distribuées.
Pour le détail du calcul de
q, nous renvoyons à l’article correspondant.
Voici les résultats que donne SPSS pour nos données :
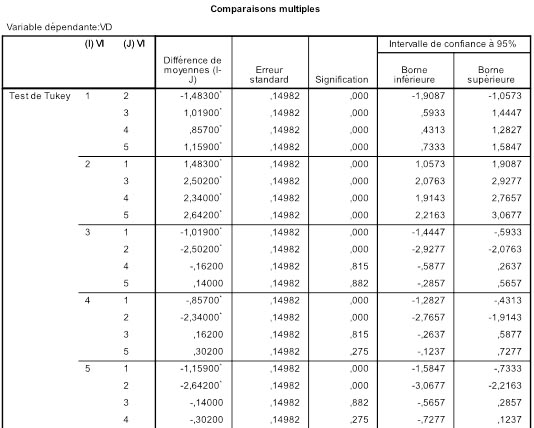
En regardant la ligne 4 du groupe 3, on voit immédiatement que le test de Tukey est plus conservateur que le LSD puisque la valeur p obtenue est .815 alors que le LSD donnait .2853 ! L'erreur standard et la différence de moyenne étant les mêmes, c'est au niveau des paramètres de la statistique q que va se faire la différence. En effet, la distribution d'échantillonnage de q admet deux paramètres, le nombre de degrés de libertés, qui ne change pas ici, et la taille de l'écart. Dans le cas présent, variances homogènes et effectifs équilibrés, nous pouvons obtenir q facilement à partir de t puisque dans ce cas
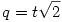
Puisque nous avons déjà calculé t plus haut (voir test LSD), on obtient donc q =-1.5292.
On entre alors dans une table de q avec 45 degrés de liberté et r =5 ou bien nous prenons un logiciel comme R dont la commande "ptukey" nous donne les valeurs p associées à la distribution d'échantillonnage de q (commande : "ptukey(1.5292,5,df=45,lower.tail = FALSE)", et nous trouvons p =0.815123, conformément au résultat présenté dans la table SPSS.
Bien sûr, on aurait pu aussi procéder en comparant le q observé qobs aux valeurs critiques d'une table. Ainsi avec r =5 et ddl =45 degrés de liberté, on lit la valeur critique au seuil α=.05, notée q .05 (5,45). On trouve q .05 (5,45)=4.018. Puisque qobs =1.529<q .05 (5,45), on sait que le test n'est pas significatif.
Attention : Dans les cas où les effectifs sont déséquilibrés ou encore lorsque les variances sont hétérogènes, voire les deux, il faut adapter le calcul de qobs selon les corrections présentées ici ).
À noter : SPSS offre une variante du HSD, dite « B de Tukey », dans laquelle la valeur critique de q est obtenue par moyennage entre la valeur critique donnée par le HSD et celle obtenue par le Student-Newman-Keuls.
3.4 La procédures REGW test Q et test F
REGW signifie Ryan-Einot-Gabriel-Welsch du nom des contributeurs successifs à l’élaboration de la procédure. Il s’agit donc d’une procédure qui utilise soit
q, la statistique d’écart studentisée, soit un test
F. Selon Howell, lorsqu'on dispose d'un logiciel pour la calculer, cette approche représente le meilleur compromis entre la nécessité de limiter l’erreur de l’ensemble des comparaisons et la nécessité de garder une puissance statistique suffisante pour rejeter l’hypothèse nulle si besoin est.
Pour réaliser ce compromis, le REGW ajuste les seuils critiques en utilisant non pas le  de la comparaison globale, mais un
de la comparaison globale, mais un  r
qui s’obtient par une formule qui requiert l’automatisation qu’offrent seulement certains logiciels de statistique (dont notamment R via le package regwq, et SPSS).
r
qui s’obtient par une formule qui requiert l’automatisation qu’offrent seulement certains logiciels de statistique (dont notamment R via le package regwq, et SPSS).
6.4. Autres tests
4.1 Un test de comparaisons de contrastes a posteriori : Scheffé
Il s’agit d’un
test de contrastes
mais a posteriori, qui permet donc de ne pas se limiter à des comparaisons deux à deux.
Il consiste à faire un test
F
standard sur l’ensemble des contrastes possibles, pas seulement les comparaisons par paires, selon la méthode vue dans l’article sur les comparaisons a priori, mais en comparant ensuite la valeur du
F
obtenu à une valeur critique différente qui permet de maintenir
p
(EC), le taux d’erreur de l’ensemble des comparaisons, à un niveau inférieur à α.
S’il y a
k
groupes en tout, qui regroupent
N
sujets, on commence par obtenir la valeur critique au seuil souhaité pour l’erreur d’ensemble α, et on la multiplie par (k
-1). On considère le résultat significatif si le
Fobs
est au moins égal au produit
Fα
(k
-1,
N
-
k) :
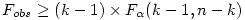
Voici les résultats de SPSS sur nos données :
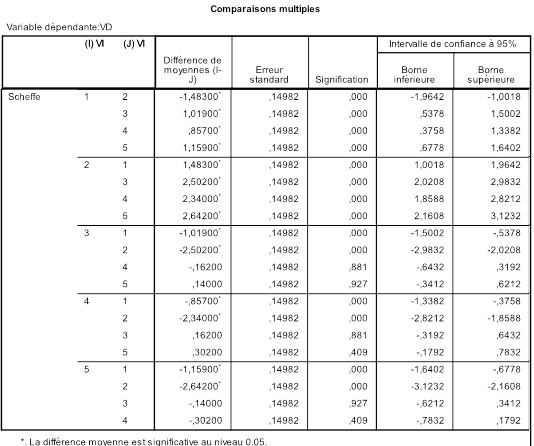
Comme il est clair sur la ligne 4 du sous-groupe 3, qui nous sert de référence depuis le début de cette page, c’est le test le plus conservateur.
Cela peut tout de même avoir un intérêt en certaines circonstances mais Howell déconseille de l’utiliser pour comparer des paires ou pour tester des hypothèses a priori.
4.2. Utilisation d’un groupe contrôle : test de Dunnett
Le test de Dunnett est spécifiquement dédié au cas où un des groupes sert de référence et va être comparé successivement à chacun des autres. Typiquement, c’est le cas d’un groupe contrôle dans une expérience. Dans cette configuration, le test de Dunnett est le plus puissant, c’est-à-dire qu’il est le plus capable de détecter une différence significative sans que l’erreur de type I pour l’ensemble des comparaisons ne dépasse le seuil alpha.
Il s’agit d’un test t classique à ceci près que les valeurs critiques de t sont obtenues par des tables particulières.
7. Questionnaire d'auto-évaluation
Ce QCM comprend 10 questions. Répondez à chaque question puis, à la fin, lorsque vous aurez répondu à toutes les questions, un bouton "terminer" apparaîtra sur la dernière question. En cliquant sur ce bouton, vous pourrez voir votre score et accéder à un corrigé.
Couleur de fond
Police
Taille de police
Couleur de texte
Crénage de la police
Visibilité de l’image
Espacement des lettres
Hauteur de ligne
Surbrillance de lien
Alignement du texte