Statistique : Tester l'association de variables

1.1. La question de la redondance

Idéalement, les VI devraient ajouter chacune un aspect différent des variations de la VD, faute de quoi l’équation comprend des termes redondants. Dans les méthodes linéaires, le contraire de la redondance entre VI est l’orthogonalité des VIs :

L’orthogonalité est le fait que deux variables soient linéairement indépendantes, c'est-à-dire que la corrélation entre deux variables orthogonales est 0. Le terme même d’orthogonalité provient de l’interprétation géométrique de la corrélation linéaire simple. On peut montrer que le cosinus de l’angle formé par les deux droites de régression d’un nuage de points à deux dimensions (cas vu plus haut) est en relation avec le coefficient de corrélation entre les deux variables. Si les deux variables sont indépendantes,l’angle que font les droites de régression est de 90° (les variables sont alors dites orthogonales), le cosinus de l'angle est alors nul et le coefficient de corrélation aussi. Inversement, si deux variables sont parfaitement et positivement liées, l’angle est nul et le coefficient de corrélation vaut 1. Ou bien si les variables sont parfaitement et négativement liées, l’angle est de 180° et le coefficient de corrélation vaut -1.

Ce qu'il faut surtout retenir c'est que si les prédicteurs (les VIs) ne sont pas des variables indépendantes (ce qui est très souvent le cas), cela peut introduire des biais dans les analyses.

1.2 Définition de la colinéarité

Géométriquement, la colinéarité est le contraire de l’orthogonalité, au sens où les deux droites de régression forment un angle non droit (le mot même de "co"-"linéarité" suggère le partage d'un certain alignement). Deux variables sont dites colinéaires lorsqu’elles sont linéairement dépendantes l’une de l’autre. Concrètement, on pourra dire que deux variables sont colinéaires dès l’instant où la corrélation entre les deux est statistiquement significative.

1.3 Colinéarité et additivité des parts de variance expliquées

La conséquence de la colinéarité entre deux VIs est que les effets respectifs de chacun de ces deux prédicteurs ne se cumulent pas simplement. En effet, si deux variables sont colinéaires, cela implique qu’elles partagent une partie de leur variance. Plus précisément, on peut distinguer une variance propre à la VI1, une variance propre à la VI2, et une variance commune aux deux. Comme toujours, la part de variance partagée par deux variables est égale au carré de leur corrélation linéaire.

Si l’on ajoutait simplement l’effet de la VI1 et celui de la VI2, sans autre forme de procès, on compterait deux fois l’effet de la variance commune aux deux et une seule fois l’effet de la variance propre à chaque VI. Prenons l’exemple du nuage de points précédent.

Nous avons vu plus haut que la régression simple de DVP par F02J explique environ 41% de la variance de cette dernière. 

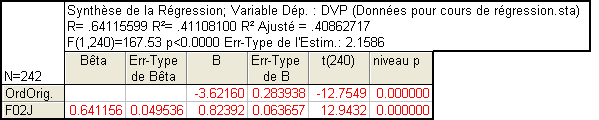
Si nous calculons la régression simple de DVP par F11VN, nous trouvons que F11VN explique environ 13% de la variance :

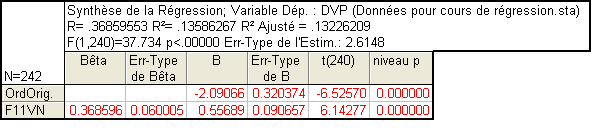
On pourrait donc s’attendre à ce qu’une régression prenant ces deux prédicteurs en compte explique 41+13=54% de la variance. Or, que trouvons-nous ?

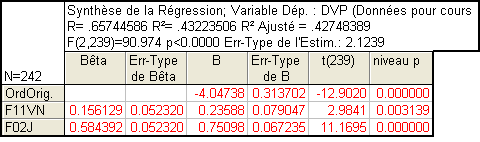
Le R² ajusté vaut .427 ce qui signifie que l’ajout de la variable F11VN explique en réalité moins de 2% de variance supplémentaire par rapport à ce qu'on avait avec F02J seule ! 

Un examen rapide de la corrélation entre les deux prédicteurs montre qu’en fait les deux VIs sont colinéaires : 

En effet, les deux variables sont significativement corrélées et donc la variance expliquée par ces deux VIs sera donc généralement inférieure à la somme des variances expliquées par chacune d'elles prise séparément.