Statistique : Tester l'association de variables

Normalité : Si le modèle est idéalement bon, alors les écarts que l’on constate entre les valeurs prédites et les valeurs observées (les résidus donc) sont entièrement imputables à des erreurs de mesure. De ce fait, les résidus doivent posséder les propriétés classiques d’une distribution normale : courbe « en cloche », symétrique autour de la valeur prédite, avec un aplatissement régulier des extrémités. En cas de violation de cette assomption, les tests de signification risquent d’être biaisés.

La première chose est de vérifier si, globalement, les résidus sont bien normalement distribués.

Sous Statistica, on peut par exemple obtenir la « droite de Henry » qui met en relation les valeurs observées des résidus (abscisses) avec des valeurs z construites sous l’hypothèse que la distribution des résidus est normale. Idéalement, on doit avoir l’identité, c'est-à-dire que tous les points du graphe doivent être situés sur la droite en rouge. Ici, le résultat est assez satisfaisant, encore qu’un très léger biais apparaît aux valeurs extrêmes.

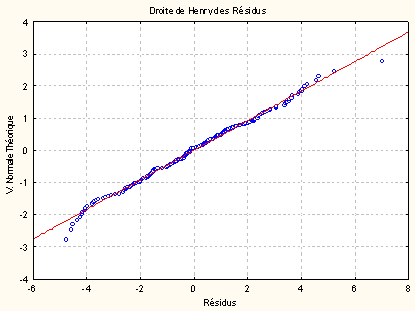
Sous SPSS, on peut demander un « diagramme P-P ». Le principe, assez similaire à celui de la droite de Henry utilisée dans Statistica, est de construire un diagramme mettant en relation la probabilité cumulée d’apparition d’une valeur avec sa probabilité théorique.

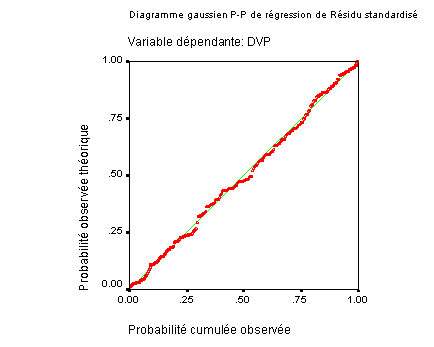
Si vous avez des doutes sur la normalité de la distribution des résidus, une stratégie qui permet d’obtenir des informations plus détaillées sur la normalité des résidus consiste à commencer par enregistrer ceux-ci comme de nouvelles variables (option disponible sous SPSS comme sous Statistica), puis à appliquer les procédures générales de test de la normalité d’une variable.