Statistique descriptive

La distribution normale s'applique dès lors qu'un grand nombre de mesures sont prises et que certaines conditions sont remplies. Malheureusement, dans de nombreuses expériences scientifiques, il est difficile, voire impossible, de procéder à de nombreuses mesures.

Un mathématicien britannique, William Gosset, a découvert au début du XIX^e siècle une statistique dont la distribution est plus représentative de ce qui se passe lorsque l'on a de petits échantillons : le t de Student.¹ Vous retrouverez cette distribution dans les cours de statistiques inférentielles, et probablement tout le long de vos études. Pour le moment, bien que nous n'étudierons pas comment la calculer, elle nous sera bien utile pour illustrer le fait qu'une distribution peut varier systématiquement en fonction de divers paramètres. Ainsi, la distribution possède une certaine forme lorsqu'elle concerne un petit nombre d'observations et tend à ressembler à la distribution normale lorsque le nombre d'observations concernées augmente.

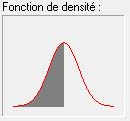
La figure ci-contre montre une distribution de t théorique pour un échantillon de 68 observations (techniquement ce paramètre est en fait une notion légèrement différente d'un simple nombre d'observations, et qu'on appelle degré de liberté et qui pour la distribution de t correspond généralement au nombre d'observations moins 1. Mais il n'est pas utile d'entrer dans ces détails pour ce cours). On voit qu'elle se distingue difficilement à l'œil nu de la distribution normale vue plus haut.

Pour mieux se rendre compte des différences subtiles induites par le paramètre que constitue le nombre de degrés de liberté, comparons deux distributions de t pour respectivement 2 et 1000 degrés de liberté :

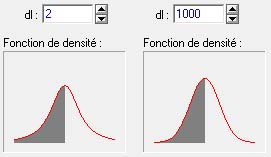
On voit aisément que la distribution à 1000 degrés de libertés (à droite) est légèrement plus haute, plus large, mais aussi que ses extrémités tendent plus vers zéro. En pratique, il devient difficile de la distinguer d'une distribution normale ordinaire.

¹ Le nom de "Student" provient du fait que William Gosset était salarié du fabricant de bière Guiness, dont la politique était alors d'interdire la publication scientifique des travaux de ses employés. Gosset a donc publié ses travaux sous le pseudonyme de Student.