Statistique descriptive

1.1. Notion de co-variation

Imaginons deux variables extrêmement et positivement liées, par exemple le salaire et le pouvoir d'achat. On observe que dès que l'une monte, l'autre monte aussi. Réciproquement, dès que la première descend, la seconde descend aussi. Bien entendu, comme nous l'avons vu dans la leçon précédente, le lien peut être très fort, mais négatif (dès qu'une variable monte, l'autre descend).

Ainsi, si nous considérons deux variables en vue d'évaluer leur degré de liaison, on peut s'intéresser à la façon dont elles co-évoluent ou non, on dira à la façon dont elles « covarient ». 

La covariation est le fait que les évolutions de chacune des deux variables présentent une certaine régularité. On l'aura compris, la covariation est un indicateur de liaison : plus la covariation est forte et régulière et plus on peut penser que les deux variables sont liées.

Une fois admis ce principe, la question qui se pose est de trouver un indicateur quantitatif de la covariation. Comment pouvons-nous faire pour mesurer la quantité de covariation qui relie deux variables ? Un premier élément de réponse nous est fourni par la notion de covariance.

1.2. Notion de covariance

Pour obtenir notre indice de covariation, il va falloir pour chaque individu statistique mesurer les variations sur une première variable X, les variations sur l'autre variable, Y, puis les combiner pour obtenir un indice agrégé. Enfin, il nous faudra agréger les mesures de covariation issues de chaque individu statistique pour obtenir une mesure globale de covariation.

1.2.1. Quantifier les variations sur chaque variable.

Imaginons que la variable ne varie pas. Tous les individus statistiques auraient donc la même valeur sur cette variable, valeur qui se trouverait aussi être la moyenne. Imaginons que cette variable commence à varier un petit peu. On trouvera donc certaines valeurs un peu éloignées de la moyenne par excès, d'autres un peu éloignées de la moyenne par défaut. Si la variable varie beaucoup, on trouvera de plus en plus d'individus ayant produit une valeur très éloignée de la moyenne. Sur cette base, il paraît donc assez naturel d'utiliser l'écart à la moyenne pour quantifier le degré de variation manifesté par un individu donné.

Soient

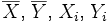
respectivement la valeur moyenne constatée sur la variable X, la valeur moyenne constatée sur la variable Y, la mesure de la variable X obtenue sur le i^ème individu, et enfin la mesure de la variable Y obtenue sur le i^ème individu.

La mesure de variation sur la variable X pour l'individu i peut donc être donnée directement par la valeur

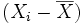
De même, la mesure de variation sur la variable Y pour l'individu  i peut être donnée par la valeur

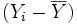
Notons que ces deux valeurs sont signées, au sens où un écart dans le sens où la valeur est plus grande que la moyenne aura un signe positif, tandis qu'une variation telle que la mesure est plus petite que la moyenne donnera un écart négatif.

1.2.2. Combiner les variations sur chaque variable.

Nous nous intéressons ici à obtenir une mesure de la liaison, donc à mettre en relation les variations sur une variable avec les variations sur l'autre variable, ce qui suppose de combiner les deux mesures précédentes. Par ailleurs, nous avons vu dans la leçon précédente qu'une liaison entre variable possédait une certaine force et une certaine direction. Il serait donc avantageux que l'indice que nous sommes en train de construire capture cette direction. Autrement dit, il ne devrait pas donner le même résultat lorsque les variations sur X et Y vont dans le même sens (par exemple lorsque les deux variables augmentent) et lorsqu'elles vont en sens contraire (par exemple, l'une monte et l'autre descend).

Une solution de combinaison très simple qui respecte ces propriétés est la multiplication :

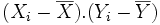
En effet, si l'on multiplie deux nombres de même signe, le produit sera positif tandis que si l'on multiplie deux nombres de signes opposés le produit sera négatif. Ainsi, le signe du produit des écarts à la moyenne sera positif si les deux mesures sur X et sur Y sont du même côté de leur moyenne, et de signe négatif si l'une est plus grande que sa moyenne tandis que l'autre est plus petite que sa moyenne.

1.2.3. Combiner les variations sur l'ensemble des sujets

Jusqu'ici, nous avons obtenu un indice qui caractérise la covariation au niveau de chaque individu. Finalement, pour avoir une vue d'ensemble de la covariation des deux variables, il nous reste donc à agréger les indices individuels en un indice global. Pour ce faire, une solution naturelle est d'utiliser la moyenne, donc de calculer la somme de chaque indice individuel puis de diviser par le nombre d'individus de la population. Cela nous donne un indice qui est la covariance des deux variables dans la population considérée :

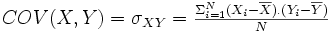
Comme vous pouvez le noter sur la formule ci-dessus, la lettre qui est utilisée pour caractériser la covariance est la lettre grecque sigma, dont nous avions vu qu'elle était utilisée pour dénoter l'écart-type d'une variable. Nous allons voir maintenant que cela n'est pas un hasard.

1.3. Relation entre covariance et variance

Que se passe-t-il si j'essaie d'estimer la covariance d'une variance avec elle-même ? Évidemment, je m'attends à trouver une liaison parfaite. Donc d'une certaine façon, la covariance d'une variable avec elle-même devrait me donner une idée de la plus parfaite liaison qu'il est possible d'avoir avec cette variable. Appliquons donc notre formule de covariance à une variable A dont on va mesurer la covariance avec elle-même. Nous aurons alors

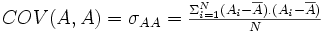
Il est clair que le terme

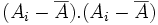
peut se réécrire 

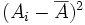
et donc que 

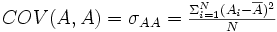
Au cours de la présente grande leçon, nous avons déjà posé la question de la quantification des variations. C'était lorsqu'il s'agissait de mesurer la dispersion d'une variable, dans l'article sur les indices de dispersion. Il est en effet assez intuitif que variation et dispersion recouvrent des concepts très similaires : plus il y a de variations, plus il y a de dispersion et réciproquement. De ce fait, si je dispose d'un indice de mesure de la dispersion, je dispose par là-même d'un indice de quantification des variations. Dans le cas d'une variable numérique, nous avons vu que l'indice pertinent était la variance dont la formule était la suivante :

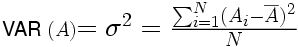
Si vous comparez les deux formules, celle de la variance et celle de la covariance d'une variable avec elle-même, vous voyez qu'elles sont rigoureusement identiques.