Statistique inférentielle et psychométrie appliquée
Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette leçon est essentielle pour comprendre les suivantes, car tous les concepts de base de la statistique inférentielle y sont expliqués.
3. La prédiction: scientifique ou actuarielle ?
3.3. Prévision actuarielle d'un événement collectif
La prévision actuarielle n'est pas destinée à la prévision d'événements singuliers, mais à la prévision d'événements collectifs. Un événement collectif réfère à une classe d'événements, ou encore, et peut-être plus exactement, à une classe de référence. Continuons avec l'exemple de Cronbach, en procédant en deux temps : d'abord de manière rétrospective, puis de manière prospective.
Si on considère les lycéens qui ont obtenu un score entre 41 et 50 points par exemple, quel est le pourcentage conditionnel (i.e., conditionnellement à la classe [41, 50]) de chaque grade ?
- 21% pour le grade A,
- 62 - 21 = 41% pour le grade B,
- 92 - 62 = 30% pour le grade C,
- 99 - 92 = 7% pour le grade D,
ce qui donne un total de 99% logiquement impossible. Les erreurs d'arrondi expliquent peut-être cette bizarrerie et nous considérerons que 8% des étudiants de cette classe ont le grade D.
Maintenant, expérimentons. On tire au sort un des lycéens de la classe et on note son grade dans le tableau suivant :
|
Tirage
|
A | B |
C
|
D
|
| 1 |
0
|
0
|
1
|
0
|
|
2
|
0
|
0
|
0
|
1
|
|
3
|
0
|
0
|
0
|
1
|
|
...
|
|
|
||
|
n
|
|
|
|
|
On obtient un lycéen qui a le grade C. On repose le nom de ce lycéen dans son urne et on recommence, pour obtenir cette fois un lycéen de type D. On repose le nom de ce lycéen et on recommence, avec le même résultat. On peut recommencer nos observations jusqu'à en avoir, par exemple, n = 2000.
On calcule alors la fréquence de chaque événement (A, B, C ou D) lorsqu'on a fait un tirage, deux tirages, trois tirages, etc. jusqu'à n tirages, et on affiche les résultats sur le graphique ci-dessous.
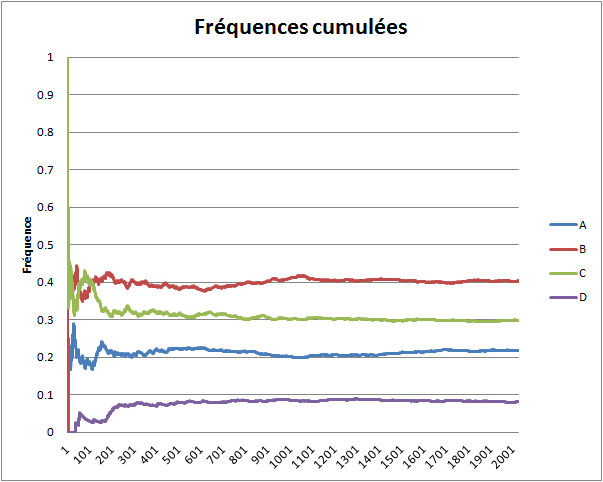
Le phénomène remarquable est la convergence de chaque série de fréquences. La série des fréquences de l'événement A converge vers la valeur de la probabilité de l'événement A, la série des fréquences de l'événement B converge vers la valeur de la probabilité de B, etc. Si on recommence toute l'expérience, on obtiendra des courbes (très probablement) différentes, mais ces courbes convergeront encore vers la valeur de la probabilité de l'événement auquel elles sont associées. Pour expérimenter par vous-mêmes à l'aide d'un simulateur informatique, cliquez ici. La théorie des probabilités explique logiquement cette nécessité.
Maintenant, tournons-nous vers l'utilisation prospective des données. En effet, les résultats que nous venons d'expliquer reposent sur la donnée de l'échantillon des lycéens, qui permet de connaître la proportion de chaque événement sur laquelle se fonde la convergence. La prévision actuarielle d'un phénomène porte sur la fréquence dudit phénomène (ou événement) -- c'est pourquoi nous parlons d'événement collectif -- et s'applique à des événements futurs. Le problème qui se pose est de savoir si la fréquence converge. Question purement métaphysique, puisqu'on ne connaît pas ladite population et donc pas la proportion des événements.
On décide alors de croire en la convergence. Muni de cette hypothèse, on peut supposer que la fréquence de A dans des échantillons de nouveaux lycéens qui ont un score entre 41 et 50 points tend vers une certaine valeur, pas forcément voisine de .21, au fur et à mesure qu'on augmente la taille de ces échantillons. Si je dois optimiser le nombre de fois où j'ai raison en prédisant un grade, je peux donc prévoir systématiquement le grade B compte tenu de ce que je connais, pourvu que j'aie affaire à un grand nombre de décisions (regardez sur les courbes combien d'observation sont nécessaires pour que les courbes ne se croisent plus). S'il s'avérait que les courbes de fréquences de très gros échantillons ne soient pas convergentes, il faudrait en déduire que le recours à la notion de loi de probabilité (i.e., l'idée que les proportions dans la population sont fixes) n'est pas fondé.
Ce type de raisonnement est utilisé par les assurances qui ajustent leurs tarifs en fonction des types de clients. Par exemple, on peut s'intéresser à la fréquence des accidents de la route en fonction du sexe et de l'âge des conducteurs, pour appliquer des tarifs avantageux aux clients appartenant aux classes les plus sûres si ces clients ne veulent pas être solidaires des clients des classes les moins sûres (ici, le lecteur aura compris que nous ne connaissons pas grand-chose en matière de politique tarifaire des assurances).