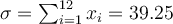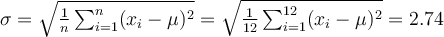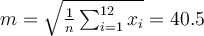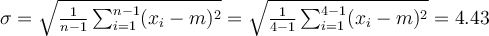Statistique inférentielle et psychométrie appliquée
 Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette leçon est essentielle pour comprendre les suivantes, car tous les concepts de base de la statistique inférentielle y sont expliqués.
8. Population et échantillons
8.4. Statistiques d'échantillon et statistiques de population
4.1. Statistiques de population
Si l'on en avait la possibilité physique, on pourrait construire une valeur mathématique, une statistique sur la population globale. Par exemple la taille moyenne. Il "suffirait" de mesurer les 8 milliards d'humains, entrer les mesures dans une gigantesque opération et en sortie l'ordinateur nous dirait sans difficulté quelle est la vraie taille de l'humain moyen (lequel n'existe pas, mais la question du rapport entre les construits de la science et leurs contreparties empiriques supposées sort du cadre du présent cours).
Nous aurons donc obtenu une Statistique de population, une mesure valable pour l'ensemble de la population. On note généralement ces statistiques avec des lettres grecques, ce dont on peut se servir comme moyen mnémotechnique pour rappeler leur caractère "idéal" plutôt que réel.
Typiquement, les moyennes de populations par exemple se notent avec la lettre grecque mu qui, en minuscule, s'écrit 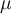 .
.
Les écarts-types de populations se notent avec la lettre grecque sigma qui, en minuscule, s'écrit 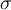 .
.
L'écart-type étant la racine carrée de la variance, les variances de population se notent souvent  .
.
À titre d'exemple, nous prendrons la population des hommes ayant marché sur la lune. À ce jour, cette population est très restreinte puisqu'elle comporte en tout et pour tout... 12 individus. Imaginons que nous nous intéressions à l'âge des individus de cette population au moment de leur sortie sur notre satellite. Nous obtenons le tableau suivant :
| Individu | Age |
| 1 | 38 |
| 2 | 39 |
| 3 | 39 |
| 4 | 37 |
| 5 | 47 |
| 6 | 39 |
| 7 | 39 |
| 8 | 41 |
| 9 | 41 |
| 10 | 36 |
| 11 | 38 |
| 12 | 37 |
À partir de ce tableau, il est facile de calculer la moyenne et l'écart-type des âges, soit
et
On a aussi la variance de notre population qui est 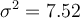
4.2. Statistiques d'échantillon
De même que l'on calcule les statistiques de population en prenant en compte tous les individus de la population cible, on calcule les statistiques d'échantillon en prenant en compte tous les individus de l'échantillon.
Pour chaque échantillon, on pourra donc calculer, par exemple, sa moyenne. On note généralement ces statistiques avec des lettres romanes. Typiquement, les moyennes d'échantillon par exemple se notent avec la lettre m (notez l'italique, correspondant aux normes de notation en vigueur en psychologie).
Il faut noter que pour des raisons techniques, la variance d'un échantillon se calcule avec une formule légèrement différente de la variance de la population : on divise la somme des carrés des écarts à la moyenne par n-1 et non par n.
Pour les besoins de l'exemple, imaginons que nous souhaitions connaître l'âge moyen des astronautes au moment de leur sortie, mais que nous ne disposions que des données pour un échantillon de 4 des 12 astronautes, les âges des autres nous étant inaccessibles. La meilleure estimation possible de l'âge moyen de la population serait donc l'âge moyen dans l'échantillon. Et la meilleure estimation possible de l'écart-type de la population serait l'écart-type de l'échantillon. Soit donc notre échantillon :
| Individu | Age |
| 4 | 37 |
| 5 | 47 |
| 6 | 39 |
| 7 | 39 |
À partir de ce deuxième tableau, il est facile de calculer les formules de la moyenne et l'écart-type des âges (revoir cours de première année), soit
Rappelons encore une fois que, pour des raisons mathématiques, on considère que l'estimation de la variance de la population à partir de la variance de l'échantillon est meilleure si l'on divise la somme des carrés par n-1 au lieu de n comme c'était le cas pour la variance de la population.Bien entendu, on imaginant que la moyenne de la population est à peu près comme la moyenne de l'échantillon, on commet une erreur d'estimation puisque cela nous conduit à évaluer l'âge de la population à 40.5 ans alors que, dans ce cas très particulier, nous savons que la vraie valeur est 39.25. Il en est de même pour la variance et l'écart-type : nous commettons des erreurs d'estimation. D'ailleurs, si nous tirons un autre échantillon, nous obtiendrons certainement des estimations légèrement différentes.
Et voilà posé un problème de la statistique : comment évaluer l'erreur commise sur l'estimation des caractéristiques de la population à partir des informations connues de l'échantillon ?
Une première idée est que les échantillons que l'on peut tirer d'une population constituent un ensemble que l'on peut étudier pour en inférer des informations sur la population. Examinons donc les relations qui existent entre les propriétés de la population et les propriétés de l'échantillon que l'on peut en tirer. La première des relations que nous allons considérer est la question du nombre d'échantillons que l'on peut tirer d'une population.
4.2. Dénombrement des statistiques d'échantillon
4.2.1. Premier facteur : la taille de la population
Soit une toute petite population d'individus, disons par exemple notre population d'individus ayant marché sur la lune. Nous l'avons vu plus, haut, chaque échantillon sera plus ou moins biaisé par rapport à la population. De plus, il y a de nombreuses façons de constituer l'échantillon.
Pour ceux qui ont le goût des mathématiques, on peut facilement dénombrer ces façons, car cela correspond au nombre de combinaisons de k individus que l'on peut tirer dans une population de n individus. Soit
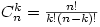
où le caractère "!" représente l'opération factorielle.
Par exemple, si nous appliquons cela à une population de, disons, 12 astronautes, et que l'on construit des échantillons de 4 personnes, le nombre d'échantillons possibles est
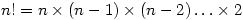
Et cela monte très très vite : avec une population de seulement 15 astronautes, on pourrait déjà tirer... 1365 échantillons de quatre individus !
4.2.2. Second facteur : la taille de l'échantillon
Le nombre d'échantillons différents que l'on peut extraire d'une population dépend d'un deuxième paramètre, à savoir la taille des échantillons, traduite par la lettre k dans la formule générale :
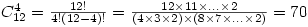
Un tableur nous donne directement la valeur cherchée au moyen de la formule suivante :
=COMBIN(n;k)
Sur une population de n sujets, on ne pourra construire qu'un échantillon de n sujets, mais on pourra construire n-1 échantillons différents de n-1 sujets. Dans l'exemple précédent, on voit facilement qu'on peut tirer 1365 échantillons de 4 sujets à partir de 15, mais on peut tirer 3003 échantillons de 5 personnes, 6435 échantillons de 7 personnes, etc. Au total, à partir de seulement 15 personnes, on peut tirer... 32767 échantillons différents !
4.2.3. Échantillonner c'est comme jouer au loto !
En fait, si l'on combine les deux facteurs précédents, on voit que de façon générale, il y a 2n façons différentes d'échantillonner une population de n individus. Partant de là, on voit que s'il s'agit d'étudier 8 milliards d'humains, le nombre d'échantillons possibles défie complètement l'imagination.
Et ne parlons même pas d'espérer réaliser l'échantillon parfait, celui qui serait parfaitement représentatif de la réalité complète. Il s'ensuit que tout échantillonnage réalisé dans la pratique peut s'apparenter à une sorte de tirage au sort dans une gigantesque urne décrivant tous les échantillonnages possibles.
Couleur de fond
Police
Taille de police
Couleur de texte