UOH / Statistique et Psychométrie en L2

A. Bref retour sur l'hypothèse expérimentale et l'hypothèse nulle.

Dans l'article sur l'hypothèse nulle, nous avons vu qu'il s'agit d'une prédiction faite sur le comportement d'une réalité donnée, prédiction ne supposant pas d'autre facteur actif qu'une simple répartition aléatoire, au hasard, des événements possibles. L'hypothèse alternative est l'hypothèse inverse : quelque cause systématique, peut être le mécanisme imaginé par le chercheur -- mais pas forcément --, est à l'œuvre. L'hypothèse du chercheur est donc un cas particulier de l'hypothèse alternative. 

Malheureusement, dans les sciences expérimentales, les choses ne sont pas aussi simples que dans les sciences exactes, et l'on dispose très rarement d'une preuve directe en faveur d'une hypothèse, ou contre une hypothèse, mais seulement de faits qui sont plus ou moins compatibles avec l'un ou l'autre des deux hypothèses.

B. Bref retour sur l'erreur de type I et le risque 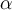$\alpha$.

Une fois qu'il a recueilli ses données, le problème du chercheur est alors le suivant : comment, à partir d'un ensemble de données, évaluer à quel degré ces données sont compatibles avec ces deux hypothèses. Une fois cette évaluation réalisée, le chercheur devra encore décider s'il peut considérer l'hypothèse expérimentale comme acceptable ou si l'on doit considérer l'hypothèse nulle comme suffisante. Bien sûr, si l'hypothèse nulle est suffisante, cela va contre l'hypothèse expérimentale en vertu du principe de parcimonie puisque l'hypothèse nulle est, par principe, plus simple que l'hypothèse expérimentale : Si H₀ n'est pas incompatible avec les données, il devient difficile de justifier de recourir à une hypothèse plus compliquée.

On voit donc que toute la problématique du test expérimental peut se ramener ultimement à un problème de décision de rejeter ou non l'hypothèse nulle*.

Puisqu'on est dans un problème de décision, et qu'il existe toujours des risques de se tromper, quatre cas sont possibles : je rejette H₀ et j'ai raison; j'accepte H₀ et j'ai raison; je rejette H₀ et j'ai tort; j'accepte H₀ et j'ai tort. Les deux derniers cas correspondent respectivement aux risques de types I et II respectivement.

Pour prendre la décision qui nous intéresse, on va donc chercher à réduire le plus possible le risque de type I. On se donne un seuil 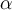$\alpha$ et on exige que la $p\leq\alpha$ pour nous autoriser à rejeter l'hypothèse du hasard. (le risque $\beta$ est moins intéressant à considérer au niveau L2, mais il sert pour des cours plus avancés).  Nous pourrons réduire le risque pris en rejetant l'hypothèse en choisissant un seuil bas pour la décision. 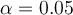Conventionnellement, on prend $\alpha=0.05$ mais dans certaines situations le chercheur peut se donner un seuil encore plus bas, .01, .005, voire même .0005.

*Rappelons ici une fois de plus qu'on n'accepte jamais une hypothèse générale empirique puisque l'on sait depuis Popper que les hypothèses générales ne peuvent être que réfutées et jamais démontrées vraies. Et, par conséquent, on ne considère jamais que H₀ est vraie, mais seulement qu'elle n'est pas réfutée, pas rejetée. À la rigueur, d'un point de vue décisionnel, on pourra la considérer comme provisoirement acceptable. Mais en aucun comme véritablement "acceptée".

C. Un exemple (très) simple du calcul du la valeur p.

Supposons que je veuille tester si une pièce est truquée. Je la jette, disons, 10 fois en l'air. Chacun sait que si elle n'est pas truquée, il y a une chance sur deux qu'elle retombe sur pile et une chance sur deux qu'elle retombe sur face. Une autre façon de le dire est de prévoir que si je jette la pièce en l'air 1000 fois, elle tombera environ 500 fois sur pile et environ 500 fois sur face. Cette prédiction ne fait appel à aucun autre mécanisme hypothétique que le seul « effet du hasard ». C'est donc un cas d'hypothèse nulle.  À l'inverse, l'hypothèse que la pièce est truquée prédit qu'ultimement la pièce va tomber toujours sur pile ou toujours sur face (on pourrait avoir des trucages plus sophistiqués, mais admettons cela pour l'exemple).

Supposons maintenant qu'ayant lancé 10 fois la pièce en l'air pour tester l'idée qu'elle pourrait être truquée, j'observe 10 fois le résultat pile. La probabilité d'avoir 10 fois de suite pile par hasard peut se calculer facilement, car à chaque lancer j'ai une chance sur deux d'avoir pile. Les lancers étant supposés indépendants, les probabilités à chaque tirage se multiplient et j'ai donc ½×½×...×½, soit 1 sur 2¹⁰ ; Autrement dit, il y a une chance sur 1024 d'observer un tel résultat si la pièce n'est pas truquée. Autrement dit, si l'hypothèse nulle est vraie, la probabilité d'avoir obtenu ce résultat est très légèrement inférieure à 0,001. Nous écrirons donc " p < 0,001 ". Ou encore si nous sommes dans un article scientifique conforme aux normes internationales de psychologie, "p<.001".

En apparence, c'est simple. Mais, seulement parce que nous sommes dans le cas très particulier où l'on sait calculer directement la probabilité d'avoir eu ce résultat en supposant que l'hypothèse nulle soit vraie. Nous allons maintenant étudier la procédure formelle de calcul qui s'applique dans le cas général qui s'appuie sur la notion de distribution.