Statistique inférentielle et psychométrie appliquée
 Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette grande leçon introduit la statistique inférentielle et la psychométrie appliquée, ceci dans la perspective de permettre aux étudiants de comprendre les enjeux épistémologiques, scientifiques et techniques de ces matières. Ces enjeux comprennent en particulier la mise au point de méthodes objectives pour l’étude de la variabilité induite expérimentalement ou observée en condition naturelle.
Cette leçon est essentielle pour comprendre les suivantes, car tous les concepts de base de la statistique inférentielle y sont expliqués.
10. Évaluer la valeur p
10.3. Calculer la valeur p par la loi normale
A. Distribution normale d’un échantillon réel
Soit une variable V quelconque contenant une série de données. Cette variable a une moyenne m et un écart-type s. Elle a aussi une distribution, à savoir que les effectifs se répartissent d’une certaine façon sur l’ensemble des valeurs possibles. Ce que l’on voit classiquement au moyen d’un histogramme comme celui-ci-dessous, qui représente les 863 notes obtenues à l’épreuve de mathématique du concours d’entrée dans une grande école d’ingénieurs (Il s’agit de données réelles que nous avons entrées dans une variable nommée « Math »).
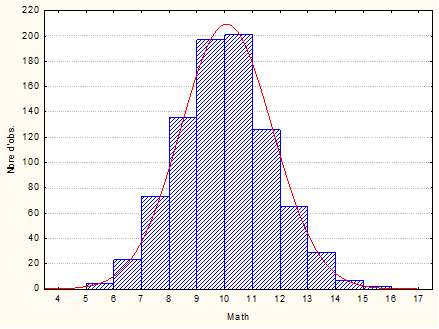
Sur l’histogramme, on voit ici apparaître en rouge l’allure de la courbe normale théorique la plus proche de la distribution de la variable V. Rappelons qu’une distribution normale théorique est caractérisée par deux paramètres, sa moyenne μ et son écart-type σ. Il suffit donc de connaître la moyenne et l’écart-type de l’échantillon pour connaître l’allure de la courbe normale qu’aurait la distribution de la population d’origine en supposant qu’elle soit normalement distribuée. Dans notre échantillon, La moyenne est m=10.0368 et l’écart-type est s=1.644482. On peut donc calculer la distribution théorique ayant ces caractéristiques-là et la comparer à la distribution observée dans l’échantillon.
Il va de soi que toutes les distributions d’échantillons ne sont pas normales, ne serait-ce que parce que les populations dont sont extraits les échantillons ne sont pas elles-mêmes toujours normales. Ainsi, par exemple, si l’on traçait la distribution des revenus en France, on obtiendrait une courbe tout à fait différente, ne serait-ce que parce que la distribution normale est symétrique autour de la moyenne alors que les revenus ne le sont pas.
On peut bien entendu s’interroger sur la meilleure façon de décider si une distribution d’échantillon peut être considérée comme normale ou non, mais nous le verrons plus loin. Pour le moment, nous admettrons que la présente distribution peut être considérée comme normale.
B. Obtention de notes z : la centration-réduction
Créons maintenant une nouvelle variable, appelée zMaths, par transformation de la variable Maths. Cette transformation sera ce qu’on appelle une standardisation, ou encore centration-réduction.
- La centration consiste pour chaque observation, à soustraire la valeur de la moyenne. Elle a pour effet que la nouvelle variable aura pour moyenne 0. Les observations qui dans l’ancienne variable avaient une valeur moindre que la moyenne vont se trouver avec des valeurs négatives tandis que celles qui étaient au-dessus de la moyenne vont se trouver avec des valeurs positives.
- La réduction consiste à diviser le résultat de la centration par la valeur de l’écart-type. Elle a pour effet que l’écart-type de la nouvelle variable est 1.
- Ainsi la nouvelle variable a pour moyenne 0 et pour écart-type 1. C’est que l’on appelle une « note z » et c’est d’ailleurs pour cela que l’on a appelé ici la nouvelle variable zMaths.
Voici l’histogramme de la variable zMaths :
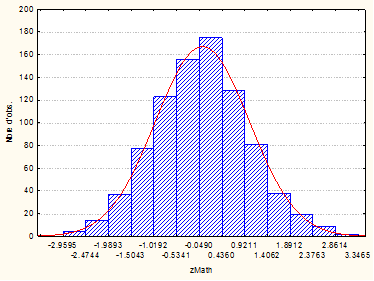
Nous avons toujours le même nombre d’observations, mais la distribution est maintenant centrée sur 0 et le nouvel écart-type est 1, ce qui affecte l’aplatissement de la courbe mais pas la symétrie autour de la moyenne. D’ailleurs, si nous centrons-réduisons une variable non normale, la transformée ne sera pas normale non plus.
L’intérêt de travailler avec des notes z est que nous pouvons maintenant mettre directement les valeurs de la variable en relation avec les propriétés connues de la loi normale. C’est ce que nous allons faire, et cela va nous permettre de connaître les valeurs-p associées à un échantillon.
C. Obtention des valeurs-p à partir des notes z
Tout le raisonnement qui suit n’est valable que dans la mesure où la distribution de la population peut raisonnablement être considérée comme normale. Nous prendrons la moyenne de l’échantillon comme estimateur de la moyenne de la population, et l’écart-type de l’échantillon comme estimateur de l’écart-type de la population. À partir de là, puisque nous avons centré-réduit, nous pouvons considérer que notre variable zMaths constitue un échantillon extrait d’une population dont la moyenne est 0 et l’écart-type 1. Sous l’hypothèse que la distribution de la population globale est normale, nous pouvons donc assumer que la variable zMaths est distribuée comme une note z normale.
C.1. Rappel de quelques propriétés de la loi normale
Que savons-nous de la distribution des notes z ? Beaucoup de choses. Pour le comprendre nous allons examiner les propriétés de la courbe en rouge, que l’on appelle la fonction de « densité de probabilité ». La surface sous la courbe représente la façon dont les effectifs sont répartis.
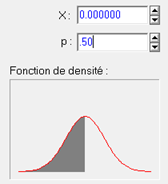
La première propriété est la symétrie : la loi normale est symétrique autour de la moyenne, donc autour de 0 pour les notes z. Par conséquent 50% des notes seront en dessous de 0 et 50% seront au-dessus. Sur le graphique ci-dessous, la zone grisée représente la surface telle que les notes sont sous le critère X qui vaut ici zéro. La valeur p=.50 traduit le fait que 50% des observations se trouveront sous cette valeur.
La symétrie à une autre conséquence : si nous prenons une valeur positive X quelconque, la probabilité d’avoir une note supérieure à X sera exactement égale à la probabilité d’avoir une note inférieure à -X. Dans l’exemple ci-dessous, nous avons pris la valeur +1. On voit que la probabilité d’avoir une note supérieure à +1 est p=.158655 (figure de droite). Si nous prenons la valeur -1 et que nous regardons la probabilité d’avoir une note plus basse, nous trouvons encore p=.158655 (figure de gauche ci-dessous).
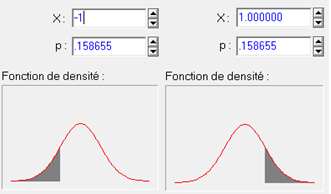
En les cumulant, on sait donc que la probabilité d’avoir par hasard une note dont la valeur absolue dépasse 1 (c’est-à-dire est plus grande que 1 ou plus petite que -1) est .317311 :
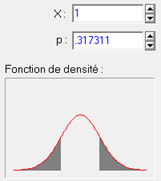
Il est très important de distinguer ce qui se passe à l’intérieur ou à l’extérieur de l’intervalle ainsi défini. En effet, comme on le voit sur la courbe, le centre de l'intervalle correspond aux valeurs compatibles avec le hasard. Plus on s’éloigne du centre et moins il est probable d’avoir obtenu la note par hasard. Si l’on a observé une valeur zobs et que l'on prend comme bornes de l’intervalle les valeurs –zobs et +zobs, les valeurs à l'intérieur de l'intervalle corroborent l'hypothèse nulle. Au contraire, celles à l’extérieur de l’intervalle sont les valeurs qui correspondent à un risque de se tromper en rejetant l’hypothèse nulle. Autrement dit, la surface sous la courbe à l’extérieur de l’intervalle est la probabilité que l’hypothèse nulle soit vraie compte tenu de la valeur z observée dans l’échantillon. C’est donc la valeur-p que nous cherchons pour l’inférence statistique. Plus elle est faible, ou ce qui revient au même, plus l’intervalle est grand, et plus le risque pris est faible.
Comment connaître la surface sous la courbe comprise à l’intérieur ou à l’extérieur de l’intervalle ?
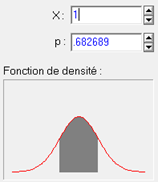
Puisque la somme de toutes les probabilités fait 1.0 par définition, la région comprise entre les deux bornes -1 et +1 contient 100%-31,7%=68,3% des observations (p= .682689) :
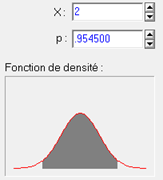
Par le même raisonnement, on trouve que 95.5% des observations sont comprises entre -2 et +2 (rappelons que pour des notes z, 1 signifie un écart-type et 2 signifie deux écarts-types). Autrement dit, il n’y a que 4.5% de chances d’observer par hasard une note z plus grande que 2 ou plus petite que -2.
À l’inverse, puisque nous sommes intéressés par le seuil alpha de 5% qui caractérise conventionnellement la significativité, on peut se demander quelle est la valeur de z qui ne laisse que 5% des observations à l’extérieur. Il s’agit de 1.96 :
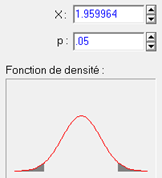
Donc si nous obtenons une statistique observée zobs, de type z (normale standardisée), dont la valeur absolue dépasse 1.96, nous avons un résultat significatif au seuil de 5%, autrement dit, il y a moins de 5% de chances qu’un échantillon ayant été extrait d’une distribution normale de moyenne 0 et d’écart-type 1 permette de calculer la note zobs. Nous dirons aussi que 1,96 est une valeur critique de z au seuil alpha de 5%.
On peut de la même façon calculer une valeur critique au seuil de 0.01 :
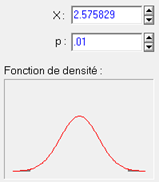
C.2. Test en unilatéral. Si l’on n’a qu'une hypothèse non directionnelle sur la valeur de z, on teste juste à quel point la valeur z observée s’écarte de 0, l'on doit prendre en compte pour le calcul de p, l’aire sous la courbe des deux côtés de la valeur critique (+z et –z). On le voit sur le graphique précédent par le fait que les deux queues de la courbe sont grisées. C’est pourquoi on qualifie un tel test de bilatéral. Mais supposons que l’on ait une hypothèse directionnelle. Par exemple, lorsque d'après l’hypothèse expérimentale, la valeur attendue de z est positive tandis qu’une valeur négative réfuterait l’hypothèse. Dans ce cas, il ne serait pas juste de compter comme représentant un risque les valeurs sous la courbe, mais seulement celles dans la queue opposée à l’attente de l’hypothèse expérimentale. Donc, et sous réserve que le résultat observé soit du côté prévu par l’hypothèse expérimentale, on peut retrancher du calcul final l’aire dans la queue du signe opposé au résultat attendu. Et puisque la distribution normale est symétrique, cela revient purement et simplement à diviser par deux la valeur-p qu’on avait obtenu en bilatéral. C’est alors un "test unilatéral". Cette possibilité peut ainsi faire passer un test du statut de non significatif en bilatéral (par exemple, p=.08) au statut de test significatif (car alors on a p=.08/2=.04 ce qui est significatif au seuil de 5%).
Il est important de savoir que la possibilité de travailler en unilatéral est subordonnée au caractère symétrique de la loi, faute de quoi, il n’y a plus aucune légitimité à diviser par deux la valeur-p obtenue.
Couleur de fond
Police
Taille de police
Couleur de texte

