UOH / Statistique et Psychométrie en L2

Supposons que nous disposions de deux corrélations r₁ et r₂. Par exemple, nous savons que chez les enfants la corrélation entre l'âge et le désir de fraises des bois est de .45 tandis que, chez les adultes, elle est de .30 (ce sont des chiffres complètement fantaisistes évidemment !). Nous voudrions savoir s'il est possible de dire statistiquement que la relation entre l'âge et le désir de manger des fraises des bois est plus forte chez les enfants que chez les adultes, comme le suggère l'écart entre les corrélations observées. Nous voulons donc savoir si la différence des deux corrélations observées peut être attribuée au hasard (hypothèse nulle) ou non. 

Lorsqu'il s'agit de comparer deux corrélations, deux éléments doivent être pris en compte :

• On ne peut calculer pas simplement la différence de 2 corrélations comme on le faisait avec des moyennes.
• Il faut distinguer le cas où les deux corrélations ont été obtenues indépendamment l'une de l'autre du cas où ces corrélations sont elles-mêmes potentiellement corrélées (par exemple lorsqu'elles ont été obtenues sur les mêmes sujets ou qu'elles impliquent une variable commune). Seul le cas indépendant est traité ici.

2.1. La transformation de Fisher

Le coefficient de corrélation r de Pearson n'est pas une variable normalement distribuée. Sa distribution est bornée à +1 et -1 alors que la loi normale est définie sur l'ensemble des nombres réels. Et, surtout, les différences entre deux corrélations n'ont pas du tout la même valeur selon les régions de l'intervalle [-1; 1] concernées. Par exemple, une corrélation de.05 et.08, l'écart, .03, ne représente pas grand-chose. Au contraire, le même écart est considérable s'il différencie une corrélation de .96 et une corrélation de .99.

La solution à cette première difficulté est assez simple à mettre en œuvre du fait que l'on peut appliquer une correction aux valeurs de r, appelée transformation de Fisher (le même que celui de l'ANOVA). Après transformation de la valeur r en note r' , la distribution obtenue est à peu près normale. La transformation est la fonction dite "arctangente hyperbolique" (aussi notée "argtanh" en langage mathématique) dont la formule est

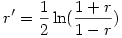
 Autrement dit, on prend le logarithme népérien (fonction "ln" sous Excel) du rapport (1+ r ) / (1- r ), et on divise le résultat par 2. Notons que sous des tableurs comme Excel ou OpenOffice Calc, on peut directement obtenir la transformation au moyen de la fonction "atanh" qui prend la valeur à transformer comme argument. On peut aussi noter des limites à cette transformation car elle n'est pas définie dans les cas où r est exactement égal à +1 ou -1 car

• on ne peut pas faire une division par 0 (or, si r =1 alors 1- r = 0)
• la fonction logarithme n'est pas définie pour la valeur 0 (or, si r =-1, alors 1+ r = 0 et le rapport vaut 0 aussi).

On peut remarquer en outre, qu'après transformation, les valeurs ne sont plus contenues dans l'intervalle [-1; +1]. Par exemple, la transformée de .90 vaut à peu près 1.47 (après arrondi à la deuxième décimale) ce qui dépasse 1.

Si nous appliquons cette transformation à la première des deux corrélations vues plus haut, nous trouvons

---

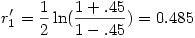
2.2. Comparer deux corrélations indépendantes

Le principe du test est très simple. Après transformation des corrélations r₁ et r₂ par la transformation de Fisher vue plus haut, on obtient r₁' et r₂'. Fisher a montré que l'on peut calculer de la façon suivante une statistique z qui suit une loi normale et que l'on peut tester en conséquence :

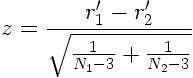
on obtient alors facilement la valeur p associée à cette note z .

Si nous reprenons notre exemple numérique (comparer r₁ =.45 et r₂ =.30), et en supposons que nous avons obtenu nos corrélations auprès de 105 enfants et 122 adultes, on voit d'abord que la transformation de Fisher, après arrondi, donne r₁ '=.485 et r₂ '=.310 et, alors, il vient

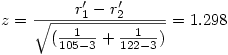
En prenant une table du z ou en utilisant un tableur, on trouve que la probabilité que z atteigne au moins cette valeur si l'hypothèse nulle est vraie est p =.194, ce qui n'est pas significatif : les deux corrélations ne sont significativement pas différentes.

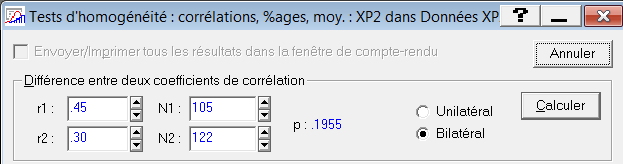
À noter : Statistica possède une fonction de comparaison des corrélations, qui donne un résultat légèrement différent à partir de la troisième décimale :