Statistique : Tester l'association de variables
Cette grande leçon présente, sous l'angle de la statistique inférentielle, les principales méthodes pour tester l'existence d'une association entre variables : corrélations de variables numériques (r
de Pearson) ordinales (
de Spearman, 
de Kendal), ou nominales (
et 
). Après un rappel de la régression linéaire simple, on introduit la corrélation partielle. Finalement, cinq articles sont consacrés à la corrélation multiple.
1. Tester la liaison entre deux variables
1.4. Tester la liaison entre deux variables ordinales
4.1. (rho) de Spearman
Rappelons que le de Spearman
(voir la section A de l'article Liaisons entre deux variables ordinales) consiste à calculer un coefficient de coefficient de corrélation classique (r
de Pearson) mais sur des données qui ont été préalablement transformées en rangs.
De ce fait, au plan inférentiel, il se teste exactement comme la corrélation simple que nous avons vue en première page du présent article.
4.1.2. Tau de Kendall
Lorsque nous avons deux variables ordinales à corréler, disons V1 et V2,nous avons deux faits deux classements. Nous avons vu dans le cours de L1 (voir la section B de l'article Liaisons entre deux variables ordinales) que le test de Kendall consiste d'abord à trier les sujets selon les valeurs croissantes de la première variable, donc à faire en sorte que quelles que soient deux observations, la valeur mesurée sur V1 de l'observation la mieux classée sera plus grande que la valeur mesurée sur V1 de l'observation la moins bien classée. On considère ensuite les mesures prises sur V2, mais toujours dans l'ordre induit par V1. On examine alors toutes les paires possibles d'observations, puis on compte les paires de données concordantes (c'est-à-dire où, comme pour la première variable, le premier nombre sur V2 est plus petit que le second nombre sur V2) et celles qui sont discordantes (celles où, contrairement à la première variable, le premier nombre sur V2 est plus grand que le secondnombre sur V2). On obtient dond deux nombres, n c le nombre de paires concordantes et n d le nombre de paires discordantes. On divise alors la différence des deux par le nombre total de paires possibles, ce qui fait :
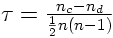
Sous l'hypothèse nulle, est nul et sa variance est
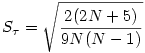
Le est distribué à peu près normalement dès que
N
>9 et donc on peut tester la valeur z
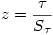
en utilisant la loi normale, comme nous l'avons fait jusqu'ici. En reprenant l'exemple vu dans le cours de L1, nous avions Tau=0.067 pour N =6 (pour l'exemple, glissons sur le fait que N n'atteint pas 9 !).
et donc z=0.067/0.3549=0.189, ce qui n'est évidemment pas significatif.